مترجم: محمدهادی شفیعیها
Theaetetus
(ت. آتن، حدود 1038ق ه/ 417ق م؛ و. آتن، 990ق ه/ 369 ق م)، ریاضیات.
تئایتتوس پسر ائوفروْنیوس از مردم سونیوم بود، كه تحصیلاتش زیرنظر تئوْدوْروسِ كورنه‌ای و در آكادمی افلاطون به پایان رسانید. با این كه هیچ نوشته‌ای از وی برجای نمانده است، تأثیری عظیم در تكامل ریاضیات یونانی داشته است. بخصوص سهمی كه وی در نظریه‌ی كمیتهای گنگ و ساختن اجسام منتظم داشته مضبوط است؛ و محتملاً او، پیش از نظریه‌ی تناسبها كه ائودوْكسوس پرداخته بوده و در كتاب پنجم «اصول» اقلیدس عرضه شده است، یك نظریه‌ی كلی برای تناسبها تنظیم كرده بوده- كه در مورد چندیهای متوافق و نامتوافق قابل كاربرد بوده است.
واژگان سودا دو مطلع به نام تئایتتوس دارد. (1)
«تئایتتوس، از مردم آتن، ستاره شناس، فیلسوف، پیرو مكتب سقراط، در هراكلیا تدریس می‌كرد. نخستین فردی است كه درباره‌ی باصطلاح پنج چند وجهی مطلبی نوشت (یا آنها را ساخت). پس از جنگ پلوْپوْنز می‌زیسته است.»
تئایتتوس، از مردم هراكلیای پوْنتوس، فیلسوف، از شاگردان افلاطون.»
برخی پنداشته‌اند كه این هر دو مطلع مربوط به شخص واحدی هستند، ولی به احتمال زیادتر، چنان كه ج. ج. آلمن (2) حدس می‌زند، دومین تئایتتوس پسر یا خویشاوند دیگر تئایتتوس اول بوده كه در زمانی كه این یكی در هراكلیا تدریس می‌كرده برای تحصیل به آكادمی در شهر زادگاهش فرستاده شده بوده است.
بخوبی آشكار است كه تئایتتوس در دیده‌ی افلاطون، از حیث تكریم و احترام، بلافاصله بعد از سقراط قرار داشته است. افلاطون در دو مكالمه‌اش، تئایتتوس و سوفیست، وی را شخصیت اصلی قرار داده است؛ و آنچه ما از زندگی تئایتتوس می‌دانیم عمدتاً از مكالمه‌ی اول استخراج شده است (3). در این مكالمه اقلیدس مگارایی پسرك خدمتگزاری را وامی دارد تا یكی از گفتگوهای بین سقراط، تئوْدوْروس، و تئایتتوس را كه افلاطون بلافاصله بعد از انجام آن در روز مواجهه‌ی سقراط با مدعیانش، یعنی در 1021ق ه/ 399ق م، ثبت كرده است برای دوستش ترپسیوْن بخواند. چون تئایتتوس در آنجا به عنوان یك «جوان» (@) مخاطب واقع می‌شود، لذا او باید جوانی مثلاً هجده ساله بوده، یعنی ولادتش در حدود 1038ق ه بوده باشد. (4)
گویند كه پدرش ثروت زیادی برای او به جا گذارده بود، ولی افرادی كه به عنوان امین برای نظارت بر آن برگزیده شده بودند آن را بر باد دادند؛ اما این امر تئاییتوس را از بخشندگی و آزادمنشی باز نداشته است. با این كه به تئایتتوس عنوان نادر یونانی @ («آقای تمام عیار») داده شده بود، آنچه هم میهنانش را تحت تأثیر قرار داده بود زیبایی فكر او بود نه زیبایی اندامش؛ زیرا او نیز، مانند سقراط، بینی پهن و چشمان برآمده داشته است. بین جوانان بسیاری كه تئوْدوْرس با آنان آشنا شده بود، وی هیچ یك را با استعدادی تا این حد شگفت انگیز نیافته بود؛ تحقیقات این جوانك مانند چشمه‌ای از روغن بود كه بی‌صدا جریان داشت. سقراط پیش بینی كرده بود كه تئایتتوس هنگامی كه به سن كمال برسد فرد برجسته‌ای می‌شود. اقلیدس [مگارایی]، در پیشگفتار بر مكالمه، شرح می‌دهد كه چگونه ناظرِ بردنِ تئایتتوسِ نزار و مردنی از اردوی كوْرینت به آتن بوده است؛ وی نه تنها پس از جنگی دلیرانه مجروح گردیده، بلكه به اسهال خونی نیز مبتلا شده بود. این واقعه می‌بایست در سال 990ق ه روی داده باشد، زیرا تنها سال دیگری كه در آن سده كورینت و آتن با هم در جنگ بوده‌اند 1015ق هـ بوده است كه مجال انجام كارهای متعدد و متنوع چند جانبی را برای تئایتتوس فراهم نمی‌آورده است. (5)
رسالهی تئایتتوس به مسأله‌ی معرفت اختصاص یافته، و سوفیست، صرف نظر از روش تعریفش، به مفهوم «عدم» تخصیص داده شده است. اگرچه تئایتتوس نقش مهمی در هر دو مباحثه دارد، دلیلی در دست نیست كه وی را فیلسوفی به معنی عادی كلمه بپنداریم. افلاطون از وجود او فقط به عنوان وسیله‌ای برای انتقال اندیشه‌هایش استفاده می‌كرد. این كه در دو مطلع واژگان سودا اصطلاح «فیلسوف» بكار برده شده چیزی را ثابت نمی‌كند، زیرا این واژگان همواره ریاضیدانان را فلاسفه می‌نامد. (6)
در خلاصه‌ی تاریخ آغازین هندسه‌ی یونان كه ائودموس گرفته است، از تئایتتوس در كنار لئوْداماسِ تاسوسی وآرخوتاسِ تارنتومی به عنوان افرادی یاد شده است كه قضایائی را افزوده و پیشرفتی به سوی گروه بندی علمیتری را موجب شده‌اند، (7) كه شور و شوق برای آن در مبحثی ریاضی كه افلاطون در تئایتتوس آورده بخوبی نشان داده شده است. (8) در این مبحث تئایتتوس ابتدا بیان می‌كند كه چگونه تئوْدوْروس برای او و سقراط جوان (مردی همنام فیلسوف) گنگ بودن اعداد
را در هر حالت جداگانه ثابت كرده است. او می‌افزاید:«چون تعداد ریشه‌ها (9) بی‌نهایت به نظر می‌آمد، به فكر افتادیم كه سعی كنیم آنها را با هم تحت یك نام گردآوریم تا بتوانیم همه‌ی ریشه‌ها را با آن اسم بنامیم.» بنابراین تئایتتوس و سقراط كهتر كلیه‌ی اعداد را به دو رده تقسیم كردند. عددی را كه می‌توانست از ضرب عوامل متساوی تشكیل و به یك مربع شبیه شود «مربعی و متساوی الاضلاعی» نامیدند. اعداد دیگر را- كه ممكن نبود از ضرب عوامل مساوی حاصل شوند، و فقط از ضرب عددی كوچكتر در عددی بزرگتر یا عددی بزرگتر در عددی كوچكتر پدید می‌آیند- به مستطیل تشبیه كردند و «اعداد مستطیلی» نامیدند. خطوطی را كه اضلاع اعداد متساوی الاضلاعی را تشكیل می‌دادند «طول» و خطوطی را كه اعداد مستطیلی را تشكیل می‌دادند «ریشه» نامیدند. و تئایتتوسِ مكالمه نتیجه می‌گیرد كه «همچنین است برای اعداد مجسّم» كه معنی آن اصلاً این است كه آنان كوشیدند كه كعبها (ریشه‌های سوم) را هم در رده بندی مشابهی قرار دهند.شاید این رده بندی اكنون پیش پا افتاده به نظر آید، ولی كشف اعداد گنگ موضوعی بود نسبتاً تازه (10)، و مستلزم قالبریزی كاملاً تازه‌ای برای ریاضیات یونانی؛ و تئایتتوس در آن ایام جوانی بیش نبود. كار پخته‌تر وی در این موضوع در شرحی بر دهمین كتاب «اصول» اقلیدس ذكر شده است، كه فقط به زبان عربی باقی مانده و معمولاً با شرحی كه نوشتن آن به پاپوس نسبت داده می‌شود یكی گرفته شده است. در مقدمه‌ی این شرح چنین آمده است: (11)
هدف كتاب دهم از رساله‌ای كه اقلیدس در «اصول» تدوین كرده بررسی كمیتّهای پیوسته‌ی موافق و نامتوافق، و گویا و گنگ است. این علم ریشه در مكتب فیثاغورس دارد ولی به دست تئایتتوس آتنی، كه به سبب استعداد ذاتیش در این زمینه و در دیگر شاخه‌های ریاضی بحق مورد تحسین بوده، پیشرفتی مهم كرد. وی كه یكی از با استعدادترین مردان بوده، به شهادت افلاطون در كتابی كه نامش از نام وی گرفته شده پژوهش در واقعیتهای موجود در این شاخه‌های علم را با شكیبایی دنبال كرده، و به عقیده‌ی من عامل عمده در استوار كردن تشخیصهای دقیق و براهین انكار ناپذیر در باب كمیّتهای مذكور در بالا بوده است. زیرا اگرچه بعداً آپولوْنیس بزرگ، كه نبوغش در ریاضیات در بالاترین درجه‌ی ممكن بود، پس از كاری شاق چند نوع قابل ملاحظه از این كمیّتها را افزوده است، این تئایتتوس بوده كه ریشه‌هائی را كه برحسب طول متوافقند از آنها كه از این حیث نامتوافقند بازشناخت، و [پاره] خطهای گنگی را كه بیشتر شناخته شده بودند برحسب معانی مختلف تقسیم كرد، و همان گونه كه ائودموسِ مشّائی بیان كرده است، «مدیال» (میانه) را به هندسه، و «بینوْمیال» (دوجمله ای) را به حساب، و «آپوْتوْم» را به همسازی یا هماهنگی تخصیص داد.
آخرین جمله‌ی بالا مفتاحی برای كارهای مهم تئایتتوس در این زمینه بدست می‌دهد. او طبقه بندی منقّح اعداد گنگی را كه در كتاب دهم اقلیدس دیده می‌شود پایه گذاری كرد؛ و بویژه تئایتتوس مدیال، بینوْمیال، و آپوْتوْم را كشف و محتملاً آنها را نامگذاری كرد. مدیال از حاصل ضرب دو طول، بینوْمیال («از دو اسم») از مجموع دو طول، و آپوْتوْم (كه مستلزم بریدن چیزی است) از تفاضل دو طول تشكیل می‌شود. بآسانی می‌توان بستگی میان مدیال و میانگین هندسی را دید، زیرا كه میانگین هندسی بین دو طول گنگِ (12) a و b هم
است و مدیال. همچنین بآسانی می‌توان بستگی بین بینوْمیال و میانگین حسابی را دید، زیرا میانگین حسابی بین دو عدد a و b برابرِ 1/2a+ 1/2b است؛ و این تعریف بینوْمیال است. بستگی میان آپوْتوْم و میانگین همساز را بآسانی نمی‌توان دید؛ ولی در بخش دوم كتاب مفتاحی به ما داده می‌شود، آنجا كه شارح به كارهای تئایتتوس برمی‌گردد و متذكر می‌شود كه اگر [مساحت] مستطیل حاصل از دو [پاره] خط مدیال بوده و یكی از اضلاع آن بینوْمیال باشد، ضلع دیگر آپوْتوْم است. این مطلب به نوبه‌ی خود یادآور گزاره‌ی 112 از كتاب دهم «اصول» اقلیدس است، و مثل آن است كه گفته شود میانگین همساز بین a و b، یعنی 2ab/a+b، را می‌توان به صورت 
بیان نمود.مطلب بالا این پرسش را پیش می‌آورد كه چه اندازه از كتاب دهم اقلیدس مدیون تئایتتوس است؟ ب. ل. وان دِر واردن، پس از یك بررسی دقیق، به این نتیجه رسیده است كه «تمام كتاب كار تئایتتوس است.» (13) ولی دلایلی چند برای این عقیده وجود دارد كه تئایتتوس تنها مدیال، بینوْمیال، و خطهای آپوْتوْم را مشخص كرده و آنها را، به گونه‌ای كه شرح عربی گویای آن است، با سه میانگین بستگی داده است؛ و جمع ده نوع دیگر طولهای گنگ، كه روی هم سیزده تا- یا، وقتی بعداً بینوْمیالها و آپوْتوْمها به اجزایی تقسیم شوند، بیست و پنج تا- می‌شود، كار خود اقلیدس است. حاشیه‌ای كه برگزاره‌ی 9 كتاب دهم («نسبت مربعهای[پاره] خطهای مستقیم متوافق از لحاظ طول به هم مثل یك عدد مربع به یك عدد مربع است...») نوشته شده به شرح زیر معتبر است، «این قضیه از كشفیات تئایتتوس است و افلاطون در رسالهی تئایتتوس بدان اشاره می‌كند، ولی آنجا به حالتهای خاص مربوط می‌شود و در اینجا به طور كلی مورد مطالعه قرار می‌گیرد.» (14) اگر تئایتتوس مؤلف تمام كتاب می‌بود، این حاشیه‌ای بی‌معنی بود.
تفاوت دقیقی كه در «خلاصه‌ی ائودموسی» بین برداشت اقلیدس از ائودوْكسوس و تئایتتوس گذاشته شده نیز قابل ذكر است. مؤلف می‌گوید كه اقلیدس «اصول را روی هم گذارده، بسیاری از قضیه‌های ائودوْكسوس را تنظیم كرده، بسیاری از قضیه‌های تئایتتوس را تكمیل نموده، و برای چیزهائی كه پیشینیانش استدلال سطحی كرده بودند دلایل رد نشدنی آورده است.» (15) آنچه حتمی به نظر می‌رسد این است كه كتاب پنجم تقریباً به طور كامل كشف ائودوْكسوس است جز در ترتیبش، ولی از كتاب دهم قسمتی متعلق به تئایتتوس است و قسمت دیگر مال خود اقلیدس. قویترین دلیل بر این عقیده كه تئایتتوس تقریباً بر نظریه‌ی گنگهای اقلیدس وقوف كامل داشته است این است كه رابطه‌ی آپوْنوْم با میانگین همساز ایجاب می‌كند كه وی از گزاره‌ی 112 كتاب دهم آگاهی داشته بوده باشد. ولی كافی است كه بدانیم متن اصلی اقلیدس احتمالاً به گزاره‌ی 111 كتاب دهم و فهرست سیزده خط مستقیم گنگ ختم می‌شود. (16)
یك مسأله‌ی دیگر مربوط به آن، دامنه‌ی تأثیر تئایتتوس است كه در كتابهای حساب «اصول» اقلیدس، هفتم تا نهم، می‌توان دید. گزاره‌ی 9 كتاب دهم بستگی دارد به گزاره‌ی 11 كتاب هشتم («بین دو عدد مربع یك عدد میانگین هندسی وجود دارد... )، و گزاره‌ی 11 كتاب هشتم به گزاره‌های 17 و 18 كتاب هفتم وابسته است (با قرارداد جدید، a:b=ac:bc و ab:ac=b:c). ه. گ تسوْیتن استدلال كرده است (17) كه این گزاره‌ها جزئی جدایی ناپذیر از یك نظریه‌ی كلی هستند كه در كتاب هفتم و در قسمت اول كتاب سیزدهم اثبات شده‌اند، و این نظریه بایستی منسوب به تئایتتوس باشد كه به منظور پایه ریزی محكمی برای نحوه‌ی پرداخت خود به گنگهاپیش كشیده است. ولی، همچنان كه ت. ل. هیث اشاره كرده (18)، واضح است كه پیش از تئایتتوس هم بقراط و هم آرخوتاس. می‌بایست از این گزاره‌ها و تعاریف مربوط به آنها در كتابهای هفتم و هشتم آگاهی داشته بوده باشند؛ و دلیلی بر دور انداختن این دید سنتی وجود ندارد كه فیثاغورسیان نظریه‌ای عددی درباره‌ی نسبت داشته‌اند كه اقلیدس آن را در كتابهای حسابش وام گرفته است. تئایتتوس تنها از یك مشت اطلاعات موجود استفاده كرده است.
كار تئایتتوس در زمینه‌ی اعداد گنگ ارتباط نزدیكی با دو خدمت عمده در ریاضیات دارد كه به وی منسوب است. تنها استفاده‌ای كه از كتاب دهم در كتابهای بعدی «اصول» اقلیدس بعمل آمده بیان اضلاعِ اجسامِ منتظمِ محاط در كره برحسب قطر آن است. در مورد چهار وجهی، هشت وجهی، و مكعب طول ضلع عملاً معین شده است؛ در مورد بیست وجهی، نشان داده شده است كه ضلع آن مینوْر است؛ و در مورد دوازده وجهی، آپوْتوْم. لذا این نكته‌ی مهمی است كه در بخشی از «واژگان سودا» (كه در بالا از آن یاد شد)، تئایتتوس نخستین كسی قلمداد شده كه درباره‌ی باصطلاح پنج جسم منتظمِ صُلب (@) «چیز نوشته» یا آنها را «ساخته» است. و نیز مهم است كه در انتهای این عبارت ریاضی در تئایتتوس می‌گوید كه او و همكارش به كار با اجسام پرداختند، به همان طریق كه با مربع و مستطیل در صفحه عمل كرده بودند. احتمالاً به اعتبار گفته‌ی تئوْفراستوس، آئتیوس (19) كشف پنج جسم منتظم را به فیثاغورسیان، و پروْكلوس (20) «پهلوی هم گذاردن» (@) «شكلهای كیهانی» را بالفعل به خود فیثاغورس نسبت می‌دهد. این اجسام را بدین علت «كیهانی» می‌نامد كه افلاطون در تیمایوس از آنها برای ساختن عالم استفاده می‌كند، (21) و تردیدی نیست كه مقصود از @ «پهلوی هم گذاشتنِ» مثلثها و مربعها و پنج ضلعیها است برای ساختن زوایای صُلب به صورتی كه در مكالمه آمده، نه به معنی ساختن صوری آنها. تئایتتوس محتملاً نخستین كسی بوده كه روش ساختمان نظری برای هر پنج جسم منتظم را تعیین كرده و نشان داده است كه چگونه باید آنها را در كره محاط كرد. یك حاشیه بر كتاب سیزدهم «اصول» اقلیدس كشف هشت وجهی و بیست وجهی را در عمل به تئایتتوس نسبت می‌دهد نه به فیثاغورسیان. (22) این امر در ظاهر شگفت انگیز است، زیرا كه هشت وجهی شكلی است مقدماتی‌تر از دوازده وجهی، كه مستلزم آگاهی بر پنج ضلعی است؛ ولی اشیای بسیاری به شكل دوازده وجهی از روزهای خیلی پیشتر از فیثاغورس پیدا شده‌اند (23). و معروف است كه هیپاسوسِ فیثاغورسی نوشته‌ای دارد درباره‌ی «ساختن كره از 12 پنج ضلعی.» (24) (در همین كتاب، اگر پیشتر از آن نبوده باشد، وی به اعداد گنگ برخورده است، و به علتِ ارتكابِ گناهِ علنی كردن آنها، به دریا افكنده شده و غرق گردیده است.) اگر فیثاغورسیان دوازده وجهی را می‌شناختند، تقریباً قطعی بود كه هشت وجهی محتملاً بیست وجهی را نیز می‌شناخته‌اند، و در آن صورت حاشیه‌ی مذكور در فوق زاید تلقی می‌شد. كار مهم تئایتتوس عبارت است از دادنِ یك روشِ ساخت نظریِ كامل از هر پنج جسم منتظم، به گونه‌ای كه ما در كتاب سیزدهم «اصول» می‌بینیم؛ و در تئایتتوس باید به عنوان منبع اصلی این كتاب نگریسته شود، اگرچه بدون تردید اقلیدس مطالب آن را به شیوه‌ی بی‌عیب و نقص خویش منظم كرده و آخرین دستكاریها را در آن بعمل آورده است. (25)
نظریه‌ی اعداد گنگ با نظریه‌ی تناسبات نیز مربوط است. عدد گنگ، زمانی كه كشف شد، مستلزم قالبریزی تازه‌ای از تناسبات فیثاغورسی بود، كه بستگی داشت به استفاده از عاملها، یعنی مقسوم علیه‌ها، و در نتیجه قابل كاربرد فقط برای مقدارهای گویا، و در حالت كلیّتر برای مقدارهای نامتوافق نیز بود. یك چنین نظریه‌ی كلی به وسیله‌ی ائودوْكسوس پیدا شده بود، و در كتاب پنجم «اصول» اقلیدس هم وارد شده است. ولی در 1312 (26) اوْسكار بِكِر تعبیر تازه‌ای از یك بخش ناروشن در «طوبیقا»ی ارسطو بدست داد (27). او اظهار عقیده كرد كه نظریه‌ی نسبتها به صورتی بسیار استادانه قبلاً از نو قالبریزی شده بوده است؛ و اگر چنین باشد، از نشانه‌ها چنین برمی‌آید كه این قالبریزی به وسیله‌ی تئایتتوس، معاصر سالخورده‌تر ائودوْكسوس، صورت پذیرفته بوده است.
در بخش مورد بحث، ارسطو می‌گوید كه در ریاضیات چیزهایی است كه بر اثر نداشتن تعریف بآسانی اثبات نمی‌شوند- مثل این مطلب كه خطی موازی با دو ضلع متوازی الاضلاع، دو ضلع دیگر و مساحت آن را به یك نسبت تقسیم می‌كند؛ ولی اگر تعریف داده شده باشد، بلافاصله مطلب روشن می‌شود، « زیرا كه مساحتها، مثل اضلاع، یك @ (آنتانائیرسیس) دارند، و این تعریفِ همان نسبت است.» معنی این واژه‌ی یونانی چیست؟ معنی اصلی آن «برداشتن و جداكردن» است، و شارحان پیش از هیث و ترجمه‌ی آكسفرد گمان می‌كردند كه «برداشتن و جدا كردن از یك كسر» است. در شكل 1، EF خط مستقیمی است موازی اضلاع AB و DC از متوازی الاضلاع ABCD، و AE و BF بترتیب همان كسرهائی از AD و BC هستند كه متوازی الاضلاع ABFE از متوازی الاضلاع ABCD است. این مطلب بنابر نظریه‌ی فیثاغورسی تناسب درست است، و بخش مورد بحث كتاب متضمن چیز معنی داری نیست. ولی بكر توجه را به شرحی كه اسكندر افروْدیسی بر این بخش نوشته است (28) معطوف می‌سازد. او واژه‌ی @ (آنتوفائیرسیس) را بكار می‌برد و می‌گوید كه این همان است كه ارسطو از «آنتانائیرسیس» در نظر داشته است. معلوم نیست كه خود این نكته مشكلی را بگشاید- ممكن است معنایش تا حد زیادی همان باشد- اما اقلیدس، چنان كه بكر متذكر شده است، هرچند این اسم «آنتوفائیرسیس» را مورد استفاده قرار نداده، در چهار جا (29) فعل «آنتوْفائیرئین» را بكار برده است- و اهمیت امر در اینجاست- و آن را برای بیانِ روندِ پیدا كردنِ بزرگترین اندازه‌ی مشترك بین دو كمیّت بكار برده است. در این روند طول كوچكتر به دفعاتِ ممكن از طول بزرگتر كم می‌شود تا این كه طولی كه باقی می‌ماند از خودش كوچكتر شود، و سپس این باقیمانده به دفعاتِ ممكن از كمیّت كوچكتر كم می‌شود تا اینكه باقیمانده‌ای كمتر از خود آن بدست آید، و این عمل پیوسته ادامه می‌یابد (@). در مورد كمیتهای متوافق، این روند پس از یك عده مراحل معین به پایان می‌رسد، ولی در مورد طولهای نامتوافق این روند هرگز پایانی ندارد. ریاضیدانی با حدّت ذهن تئایتتوس در می‌یابد كه این عمل ممكن است آزمونی برای متوافق بودن باشد (چنان كه در گزاره‌ی 2 كتاب دهم «اصول» اقلیدس آمده است) و با قبول یك تعریف نسبت براساس این آزمون توانسته است نظریه‌ی تناسبی قابل كاربرد در كمیّتهای متوافق و به همان اندازه در كمیّتهای نامتوافق بدست آورد. (30)
ممكن است كه چنین نظریه‌ای كلی پیش از ائودوْكسوس به وسیله‌ی شخص دیگری غیر از تئایتتوس پرورده شده باشد، ولی نظر به صلاحیت آشكار تئایتتوس و علاقه‌اش به مقادیر گنگ، او محتملترین فرد است. این اسناد حتی معتبرتر می‌شوند اگر توضیح تسوْیتن در باب چگونگی اثبات گنگ بودن اعداد
به وسیله‌ی تئودوْروس را بپذیریم (نگاه كنید به مقاله‌ی تئودوْروسِ كورِنه‌ای)؛ زیرا كه بنابر حدس وی تئوْدوْرس این روش را در هر مورد خاص بكار برده است، و تئودوْروس معلم تئایتتوس بوده است. با این كه سند مستقیمی دال بر این كه تئایتتوس این نظریه‌ی تناسبِ قبل از ائودوْكسی را پیدا كرده باشد در دست نیست، ظنّ قوی له وی زیاد است؛ و همه‌ی مفسران جدید را متقاعد ساخته است.معلوم نیست كه آیا تئایتتوس كشف دیگری جز در این سه زمینه داشته است یا نه. در «خلاصه‌ی ائودموسی»، پروْكلوس می‌گوید: (31) «هرموْتیموسِ كوْلوْفونی تحقیقاتی را كه به وسیله‌ی ائودوْكسوس و تئایتتوس آغاز شده بود پیش برد؛ قضایای زیادی را در «اصول» كشف كرد، و قسمتی از نظریه‌ی مكانها [ی هندسی] را گرد آورد.» با این كه روشن است كه تئایتتوس ریاضیات را نزد تئوْدوْروس فراگرفته است، معلوم نیست كه این كار را در كورِنه انجام داده یا در آتن. ممكن است بپذیریم كه او زمانی در هراكلیا تدریس می‌كرده، و ممكن است معلم هراكلیدس پوْنتیكوس نیز بوده باشد. (32)
پی‌نوشت‌ها:
1. واژگان سودا، ویراسته‌ی آدا آدلر، یكم، قسمت 2 (لایپ تسیش، 1931)، θ93 و 94، ص 689. 6-9.
2. «تئایتتوس»، از ج. ج. آلمن، در Hermatena، 6 (1887)، 269-278، تجدید چاپ در Greek Geometry From Thales to Euclid («هندسه‌ی یونانی از تالس تا اقلیدس»، لندن-دابلین، 1889)، 206-215.
3. تئایتتوس، از افلاطون در Platonis opera («مجموعه آثار افلاطون»)، ویراسته‌ی ج. برنت، یكم (آكسفرد، 1899)، 142a-148b؛ كتابخانه‌ی آثار قدیمی لوْب، آثار افلاطون، ویراسته‌ی هـ. ن. فاولر، هفتم (لندن- كیمبریج، مسچوسیتس، 1921؛ تجدید چاپ 1967)، 6. 1-27. 24.
4. ولادت تئایتتوس معمولاً در 1036ق هـ، یا حتی اندكی دیرتر در 1034ق ه، قرار داده شده است، كه سن وی را در 1020 ق ه به بیشتر از شانزده سال نمی‌رساند؛ ولی مواردی كه در A Greek-English Lexicon («واژگانی یونانی- انگلیسی»)، اثر هـ. لیدل، ر. اسكات، و هـ. استیوئرت جوْنز (آكسفرد، 1940)، ذكر شده است؛ @ و @ آشكارا نشان می‌دهند كه یك دختر یا پسر جوان (@) نبایستی كمتر از هجده سال داشته باشد و ممكن است بیست و یك ساله باشد. جمله‌ای را كه در Chronicle («شرح وقایع») ائوسیبوس آمده- و در برگردان به لاتینی و ارمنیِ یروْمه محفوظ مانده است- Sancti Heironymi interpretation chronicae Eusebii Pamphili («تفسیر هیئروْنوموس قدیس از ‘ شرح وقایع’ ائوسبیوس پامفیلیایی»)، در Patrologia Latina، ویراسته‌ی ژ. پ. مینی، جلد بیست و هفتم = قدیس هیئروْنوموس، جلد هشتم (پاریس، 1846)، ستونهای 453-454 و شدت فعالیت تئایتتوس را در سومین سال اوْلیمپیاد 85 (1059ق ه/ 438ق م)قلمداد كرده است، باید به عنوان مطلبی خطا رد كرد. - گفته‌ی ائوسبیوس را ژوْرش زونتسلوس در Corpus scriptorium historiae Byzantinae («مجموعه‌ی نوشته‌های تاریخی بیزانسی»)، ویراسته‌ی ب. گ. نیبور، بخش 701؛ و Georgius Syncellus et Nicephorus، ویراسته‌ی گ. دیندوْرف، یكم (بون، 1829)، ص9. 471، تكرار كرده است.
5. یكی از دستاوردهای عمده‌ی اِوا زاكس در سخنرانی افتتاحیه‌ی پیشگامانه‌اش [هنگام دریافت درجه‌ی دكتری]، با عنوان De Theaeteto Atheniensi mathematic («درباره‌ی ریاضیات تئایتتوس آتنی»، برلین، 1914)، 16-40، آن است كه این نكته را به نحوی انكارناپذیر، برخلاف نظر ا. تسِلِر و دیگران، ثابت كرده است.
6. ولی مَلكم س. براون، در مقاله‌ی «تئایتتوس: معرفت به مثابه‌ی فراگیری پیوسته»، در JHP، 7 (1949)، 359، بر این باور است كه تئایتتوس «هم بر جریان ریاضیات و هم بر جریان فلسفه مؤثر بوده است.» براون، در همان جا، ص 69، برای تأیید عقیده‌ی خود گفته‌ی زاكس (از اثر یاد شده در حاشیه‌ی 5) را ذكر می‌كند كه: ille revera philosophus fuit perfectus (درواقع فیلسوفی كامل است)؛ ولی جای تردید است در این كه منظور زاكس از این عبارت لاتینی این بوده باشد كه تئایتتوس الزاماً حكیمی در فلسفه‌ی اولی بوده است. براون به این گفته‌ی تئایتتوس در آغاز صحبتش با سقراط استناد می‌كند كه: «هرگاه من اشتباه كنم، تو خطای مرا اصلاح كن». (تئایتتوس، 146c)، براون در كار ریاضی تئایتتوس جریانی از تقریبات متوالی می‌بیند، كه ممكن است به عنوان «متضمن خطاهائی كه تصحیح شده‌اند» تلقی شود. و نیز معتقد است كه در مبحث معرفت شناختی مطلب مشابهی وجود دارد: «بحثی درباره‌ی عقاید، اگر خوب هدایت شود، حتی اگر در وصول به یك جواب نهایی ناموفق باشد، باز موجب بهبودی (حتی بهبودی نامشخص) در عقیده می‌شود»؛ و بر این باور است كه در این مكالمه لااقل افلاطون تا حدی به این نظر تئایتتوس تسلیم می‌شود كه «معرفت عبارت است از فراگیری پیوسته» (ص 379).
7. In primum Euclidis از پروْكلوس، ویراسته‌ی گ. فریتلاین (لایپ تسیش، 1873؛ تجدید چاپ، هیلدسهایم، 1967)، ص 66. 14-18؛ ترجمه‌ی انگلیسی به قلم گلن ر. ماروْ، با عنوان Proclus:A Commentary on the First Book of Euclid`s Elements («پروكلوس: شرحی بر كتاب اول اصول اقلیدس»، پرینستن، 1970)، ص 54. 11-14.
8. تئایتتوس، آثار افلاطون، ویراسته‌ی ج. برنت، یكم (آكسفرد، 1899)، 147c-148b؛ كتابخانه‌ی آثار قدیمی لوْب، افلاطون، ویراسته‌ی هـ. ن. فاولر، هفتم (لندن-كیمبریج، مسچوسیتس، 1921؛ تجدید چاپ، 1967)، ص 24. 9-27. 24.
9. واژه‌ی یونانی آن @ است، كه در تاریخی مؤخّر فقط می‌توانسته است به معنی «مربعات» باشد؛ ولی در اینجا به نظر می‌رسد به معنی «ریشه‌ها» باشد، و تنها می‌توانیم چنین فرض كنیم كه در آن مرحله‌ی اول این اصطلاح در ریاضیات یونان تثبیت نشده بود. لزومی ندارد كه با پوْل تانری («در باب زبان ریاضی افلاطون» در AFLB، 1 [1884]، 96، تجدید چاپ در MSc، 2 [1912]، 92) واژه‌ی @ را بی‌آنكه نسخه‌ی خطی معتبری بر آن دلالت كند با واژه‌ی @، كه اصطلاحی است فنی كه بعداً به معنی ریشه‌ی دوم وضع شده است، عوض كنیم. برای یك بحث جامع از تعبیری متفاوت، - Anfänge der grieschichen Mathematik («آغاز ریاضیات یونانی»)، از آرپاد سابوْ (مونیخ- وین، 1969)، 14-22، 43-57. سابوْ بر این عقیده است كه @ به معنی Quadratwert eines Rechtecks («مقدار مربع یك مستطیل»)، یعنی مربعی است كه مساحتش هم ارز با یك مستطیل باشد. این تعبیر جاذبه‌هائی دارد، ولی این واقعیت كه افلاطون به طور قاطع @ را به عنوان @، «خطوط»، تعریف می‌كند و @ را در مقابل @، طولی گویا، قرار می‌دهد، تعبیر فوق را بی‌ثمر می‌سازد. ولی سابوْ ثابت می‌كند كه @ به طور كلی نمی‌تواند به معنیِ توان باشد.
10. ولی نه به تازگی زمان خودِ افلاطون. حتی اگر آن آتنی بیگانه در كتاب «قوانین» با افلاطون یكی گرفته شود، از این گفته‌ی وی @ (819d 5-6( نتیجه گرفتن‌ِ این كه اعداد گنگ تا سده‌ی چهارم ق م كشف نشده‌اند زیاده روی است. و نیز عبارت «فیثاغورس موضوع اعداد گنگ را كشف كرده» (@) كه در «خلاصه‌ی ائودموسی»، در پروْكلوس، همان اثر، ص 19. 12-65 آمده است باید خطا باشد، و تقریباً قطعی است كه خطای متنی از گرفتن @ به جای @ («تناسبات») ناشی شده است. بنابر سنت یونانی، تقریباً قطعی است كه وجود طولهای گنگ را هیپاسوس متاپوْنتومی در ربع سوم سده‌ی یازدهم ق. هـ/ نیمه‌ی سده‌ی پنجم ق م كشف كرده بوده است. بهترین بحث در باب این تاریخ در مقاله‌ی «كشف نامتوافق بودن به وسیله‌ی هیپاسوس متاپوْنتومی» در Studies in Presocratic Philosophy («مطالعاتی در فلسفه‌ی پیش از سقراط»)، ویراسته‌ی دیوید ج. فرلی و ر. ا. الن، یكم (لندن- نیویوْرك، 1970)، 382-412، صورت گرفته است. برای كوششی در اثبات وقوع این كشف در سالهای اول سده‌ی دوازدهم ق هـ/ سالهای آخر سده‌ی پنجم ق م، رجوع كنید به Platon und die sogennaten Pythagoreer («افلاطون و مدعیان فیثاغورسی بودن»)، اثر اریك فرانك (هاله، 1923). آرپاد سابوْ، در اثری كه قبلاً از آن یاد شد، ص 60-69، 111-118، 238، سعی دارد كه، در مقابله با این نظریه‌ی رایج كه عددهای گنگ از مطالعه‌ی قطرهای مربع پس از كشف «قضیه‌ی فیثاغورس» نتیجه شده‌اند، نشان دهد كه اعداد مذكور ضمن مطالعه‌ی واسطه‌ی هندسی كشف گردیده‌اند.
11. این ترجمه عمدتاً براساس ترجمه‌ی ویلیام تامسن و گوستاف یونگه در «شرح پاپوس بر كتاب دهم اصول اقلیدس»(كیمبریج، مسچوسیتس، 1930؛ تجدید چاپ، نیویوْرك، 1968)، 63 صورت گرفته است؛ ولی «توانها»ی آن، (یعنی مربعها)، اگرچه ترجمه‌ی صحیح از عربی است، تغییر داده شده است، زیرا به نظر می‌رسد كه معنی آن «ریشه‌ها» باشد. ابهام واژه‌ی یونانی @ پیش از آنكه اصطلاح تثبیت شده‌ای شود، در زبان عربی منعكس شده است.
12. مفهوم اقلیدسی (دهم، تعریف 3) را، كه یك [پاره] خط راست ممكن است گویا باشد ولی فقط مربع آن با یك [پاره] خط راست گویا متوافق باشد، به تئایتتوس نسبت دادن از قراین موجود گام فراتر گذاشتن است؛ منظور اقلیدس این است كه اگر r یك [پاره] خط مستقیم گویا، و m و n عددهای صحیح، و m/n غیرممكن التحویل بوده مربع نباشد، آنگاه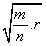 
گویا است. ت. ل. هیث می‌گوید: «چنین به نظر می‌رسد كه در اینجا اصطلاحات اقلیدس همان قدر با اصطلاحات پیشینیانش تفاوت داشته است كه با اصطلاحات امروز ما تفاوت دارد»، و بجا، عبارت افلاطون (به پیروی از فیثاغورسیان) در كتاب جمهور، 546c، 4-5؛ @ («قطر گنگ به طول پنج») به جای قطر مربعی به ضلع پنج واحد را نقل می‌كند؛ یعنی
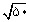، همان گونه كه برای ما گنگ است، برای افلاطون و احتمالاً برای تئایتتوس نیز گنگ بوده است، در حالی كه اقلیدس آن را «گویا ولی متوافق فقط در حالت مربع بودن» می‌خوانده است. اوا زاكس در Dif fünt platonischen körper («پنج جسم افلاطونی»)، 105، نظری مخالف دارد، ولی بدون دلایل رضایتبخش.
13. Science Awakening («بیداری علم») از ب. ل. وان دِر واردن، چاپ دوم (خروْنینگن، 1956[؟])، ص 172. او بتفصیل می‌نویسد: «آیا همان تئایتتوسی كه مدیال، بینوْمیال، و آپوْتوْم را مطالعه كرده ده طولِ گنگ دیگر را هم تعریف و بررسی نموده است؟ یا این ده طول گنگ بعداً وارد شده‌اند؟ به نظر من، همه‌ی اینها كار یك ریاضیدان است. زیرا كه مطالعه‌ی 13 طول گنگ یك واحد است. یك اندیشه‌ی بنیادی بر سراسر كتاب حاكم است، و در همه‌ی حالات روشهای واحدی در استدلال بكار رفته‌اند. گزاره‌های 17 و 18 كتاب دهم، در باب اندازه پذیری ریشه‌های یك معادله‌ی درجه‌ی دوم، پیش از وارد كردن بینوْمیال و آپوْتوْم آمده‌اند، ولی تا زمانی كه طولهای گنگ عالیتر در صحنه ظاهر نشده‌اند مورد استفاده قرار نگرفته‌اند. نظریه‌ی بینوْمیال و آپوْتوم تقریباً به گونه‌ی اجتناب ناپذیری با نظریه‌ی اعداد گنگ عالیتر درهم بافته شده‌اند. لذا- تمام كتاب كار تئایتتوس است». نتیجه گیری دنبال نمی‌شود. وحدت ممكن است نتیجه‌ی كار خود اقلیدس باشد كه برخی از قضایای قبلاً ثابت شده را بكار برده، اصلاحاتی از خود افزوده، همان گونه كه پروْكلوس ثابت كرده، همه را به یك كل بدل كرده است. تقسیم طولهای گنگ به مدیال، بینوْمیال، و آپوْتوْم را كاملاً می‌توان از تقسیمات جزئی به طولهای گنگ پیچیده‌تر بخوبی جدا كرد. درست بودن این مطلب كه گزاره‌های 17 و 18 كتاب دهم تا پس از وارد كردن بینوْمیال و آپوْتوم مورد استفاده قرار نگرفته‌اند چیزی را ثابت نمی‌كند، زیرا این گزاره‌ها در وضع منطقی صحیح قرار گرفته‌اند: تا آنجا كه به این امر مربوط است، تمامی كتاب دهم هم تا كتاب سیزدهم مورد استفاده واقع نشده است؛ ولی، درواقع گزاره‌ی 18 كتاب دهم در گزاره‌ی 33 همان كتاب بكار برده شده، در حالی كه بینوْمیال تا گزاره‌ی 36 كتاب دهم و آپوْتوْم تا گزاره‌ی 73 آن كتاب دخالت داده نشده است.
14. Euclidis opera omnia («مجموعه آثار اقلیدس»)، ویراسته‌ی ی. ل. هایبرگ و ه. مِنگه، پنجم (لایپ تسیش، 1888)، حاشیه‌ی 62 در كتاب دهم «اصول»، ص 450. 16-18 دلیل مقنعی وجود دارد برای اینكه بپذیریم شارح پروْكلوس است. - Untersuchungen über die neu aufgefundenen Scholien des Proklus Diadochus zu Euclids Elementen («بررسیهائی درباره‌ی حاشیه‌های تازه یافته شده از پروكلوْس دیادوْخوس بر اصول اقلیدس»)، از هـ. كنوْشه (هرفوْرت، 1865)، ص 24؛ و «ناگفته‌هایی در مورد اقلیدس»، از ی. ل. هایبرگ، در Herm 38 (1903)، ص 341.
15. پروْكلوس، مأخذ یاد شده، ص 68. 7-10؛ ترجمه‌ی انگلیسی در همان مأخذ، ص 59. 19-23.
16. ی. ل. هایبرگ دلایل قاطعی برای بین دو هلال گذاردن گزاره‌های 112-115 در «مجموعه‌ی آثار اقلیدس»، ویراسته‌ی ی. ل. هایبرگ و هـ. منگه، پنجم، ص هشتاد و پنج، ارائه می‌دهد و نتیجه می‌گیرد كه:
«non dubito,quin hae quoque propositiones 112-115 e doctrine Apolonii promptae sint;nam antiquae sunt et bonae,hoc saltim constare putaverim eas ab Euclide scriptas non esse».
17. مقاله‌ی« درباره‌ی ساختمان كتابهای حساب ‘ اصول’ اقلیدس و رابطه‌ی آنها با مسأله‌ی اعداد گنگ»، از ه. گ. تسوْیتن در Oversigt over der kongelige Danske Vides cabernes Selskabs Forhandlinger (1910)، 395-435.
18. A History of Greek Mathematics («تاریخچه‌ای از ریاضیات یونان»)، از تامس هیث، یكم (اكسفرد، 1921)، 211.
19. Plactia، از آئتیوس، دوم، 6، 5، در Doxographi Graeci، اثر هـ. دیلس (برلین، 1879)، ص 334؛ و Die Fragmente der Vorsokratiker («قطعاتی از فیلسوفان پیش از سقراط») ویراسته‌ی هـ. دیلس و و. كرانتس، چاپ ششم، یكم (دابلین-زوریخ، 1951؛ تجدید چاپ، 1969)، ص 408. 8-12.
20. پروْكلوس، اثر مذكور در حاشیه‌ی [7]، ص 20. 21-65؛ ترجمه‌ی انگلیسی، همان اثر، ص 53. 5. ماروْ این واژه‌ی یونانی را «structure» (ساختار) ترجمه كرده است.
21. تیمایوس، از افلاطون 55c-53c؛ «آثار افلاطون»، ویراسته‌ی ج. برنت، چهارم (آكسفرد، 1915)؛ كتابخانه‌ی آثار قدیمی لوْب، افلاطون، تیمایوس و غیره. ویراسته‌ی ر. ج. بری (لندن- كیمبریج، مسچوسیتس، 1929؛ تجدید چاپ، 1966)، ص 126. 16-134. 4.
22. «مجموعه آثار اقلیدس»، ویراسته‌ی گ. ل. هایبرگ و هـ. منگه، پنجم (لایپ تسیش، 1888)، حاشیه‌ی 1 در كتاب سیزدهم «اصول»، ص 654. 1-10.
23. تاریخ یكی از آنها، كه در 1264 در موْنته لوْفّا در كوْلّی ائوگانئی نزدیك پادوئا كشف شده و منشأ اتروریایی دارد، بین 1000 و 500 ق م است («درباره‌ی تاریخ چندوجهیها و ارقام»، از ف. لیندمان، در SBAWM، 26 [1897]، 725).
24. De communi mathematica scientia («مدخلی بر علوم ریاضی»)، از ایامبلیخوس، ویراسته‌ی ن. فستا (لایپ تسیش، 1981)، 77. 18-21؛ De vita Pythagorica («زندگی فیثاغورس»، از همو، 18. 88، ویراسته‌ی آ. ناوك (لایپ تسیش، 1884؛تجدید چاپ، 1965).
25. اوا زاكس، در ضمن یك بحث كامل در «پنج جسم افلاطونی» (برلین، 1917) می‌گوید (ص 105) كه منشأ ساختن پنج جسم موضوع كتاب سیزدهم «اصول» اقلیدس، 13-17، كار تئایتتوس است. او با هـ. فوْكت در BMat، 9، دوره‌ی سوم (1908-1909)، ص 47، در مخالفت با پوْل تانری موافق است، آنجا كه در La géométrie Grecque («هندسه‌ی یونانی»، پاریس، 1887)، ص 101، ساختن پنج جسم را به فیثاغورسیان نسبت می‌دهد در حالی كه محاسبه‌ی نسبت اضلاع به شعاع كره‌ی محیطی را از آنِ تئایتتوس می‌شمارد. او و فوْكت می‌پرسند: چگونه ممكن است كه ساختن دقیق این جسم بی‌اطلاع قبلی از این رابطه صورت گیرد؟ این پرسش كه چه اندازه از كتاب سیزدهم كار تئایتتوس است با این مسأله‌ی دشوار پیوند دارد كه چه قدر از آن، اگر هست، متعلق به آریستایوس است كه هوپسیكلس در اثر خود، به نام كتاب چهاردهم «اصول»، ویراسته‌ی ی. ل. هایبرگ و هـ. منگه، جلد پنجم، ص 22. 23-6، به عنوان مؤلف كتابی تحت عنوان «مقایسه‌ی پنج شكل»، به وی اشاره كرده است، و آیا این آریستایوس را باید با آریستایوس مهتر، مؤلف كتابی سازنده درباره‌ی مكانهای هندسی در فضا، یعنی قطوع مخروطی، یكی دانست. ت. ل. هیث، در The Thirteen Books of Euclid`s Elements («سیزده كتاب اصول اقلیدس»)، سوم (كیمبریج، 1908؛ چاپ دوم، 1925؛تجدید چاپ، نیویوْرك، 1959)، ص 439، به پیروی از ك. آ. بِرچنایدر ← در Die Geometrie und Geometer vor Euklides («هندسه و - هندسه دانان پیش از اقلیدس»، لایپ تسیش، 1870)، ص 171، چنین نظر داده است كه «چون كتاب آریستایوس جدیدترین و آخرین اثری بوده كه در آن پیش از زمان اقلیدس به این موضوع پرداخته شده بوده است. ما در كتاب سیزدهم اقلیدس دست كم مروری بر بعضی از رئوس مطالب آریستایوس داریم»؛ ولی اوا زاكس، در اثر یاد شده، ص 107، این نتیجه گیری را رد می‌كند.
26. «مطالعات شماره‌ی 1 ائودوْكسوس: یك آموزه‌ی مقدم بر ائودوْكسوس درباره‌ی تناسب، و پیگیری آن به وسیله‌ی ارسطو و اقلیدس»، نوشته‌ی اوْسكار بِكِر، در QSG، 2B، (1933)، 311-333. هـ. گ. تسوْیتن در مقاله‌ی «Hvorledes Mathematiken Tiden fra Platon til Euklid» در KDVS، 5 (1915)، 108، و ا. ی. دیكسترهویس، در De Elementen van Euclides («درباب كتاب اصول اقلیدس»، یكم، خروْنینگن، 1929)، 71، قبلاً تا حدی به این نظریه مستقلاً اشاره كرده‌اند؛ خود بكر در Das Mathematische Denken der Antike («تفكرات ریاضی دوران باستان»، گوْتینگن، 1957)، ص 103، حاشیه‌ی 25، به آن اعتراف كرده است. بكر موفق نشد ت. ل. هیث را در Mathematics in Aristotle («ریاضیات در آثار ارسطو»، آكسفرد، 1949؛ تجدید چاپ، 1970)، 80-83، متقاعد سازد؛ هیث با نبودن قراین تأیید كننده توانسته است «به مقاله‌ی بكر فقط به عنوان اندیشه‌ای بسیار شایان توجه نگاه كند» (ص83). نوشته‌ی بكر به وسیله‌ی ك. رایدِ مایستر در Das exakte Denken der Griechen («تفكرات دقیق یونانیان»، هامبورك، 1949)، ص 22، و به وسیله‌ی آرپاد سابوْ در مقاله‌ی «سندی اصیل برای آموزه‌ی تناسب مقدم بر ائودوْكسوس»، در ABeg، 9 (1964)، 151-171، و در Anfänge der griechischen Mathematik («آغاز ریاضیات یونانی»، مونیخ- وین)، 134-135، 180-181، نیز مورد انتقاد قرار گرفت. اما نظریه در رساله‌ای در لیدن با عنوان Euclid`s Conception of Ratio as Criticized by Arabian Commentators («دریافت اقلیدس از نسبت، آن گونه كه شارحان عرب نقد و بررسی كرده‌اند»)، نوشته‌ی ا. ب. پلوئنی (روْتردام، 1950)، مورد پشتیبانی واقع شد. بكر انتقادها را در ABeg، 4 (1959)، ص 223، رد كرد، و در كتابش به نام Grundlagen der Mathematik in Geschichtlicher Entwicklung («مبانی ریاضیات در تكامل تاریخی»، بوْن، 1954؛ چاپ دوم، 1964)، از نظریه‌ی خود دفاع نمود. نظریه‌ی بكر از طرف ب. ل. وان دِر واردن، در «بیداری علم»، چاپ دوم (خروْنینگن، 1956[؟])، 175-179؛ و كورت فوْن فریتس در مقاله‌ی «كشف نامتوافق بودن به وسیله‌ی هیپاسوس متاپوْنتومی» در «مطالعاتی در فلسفه‌ی پیش از سقراط»، ویراسته‌ی دیوید ج. فرلی و ر. ا. آلِن، یكم (لندن، نیویوْرك، 1970)، 408-410، بویژه حاشیه‌ی 87، صمیمانه مورد استقبال قرار گرفت؛ ولی این اظهار وی كه هیث «هنوز تعریف را ‘ مابعدالطبیعی’ می‌نامد» نادرست است؛ زیرا هیث گفته است كه این تعریف «(چنان كه از گفته‌ی بَروْ برمی‌آید) مابعدالطبیعی» بوده، و در هر حال این مطلب، پیش از آن كه نظریه‌ی بكر بیان شود، در «سیزده كتاب اصول اقلیدس»، دوم (كیمبریج، 1908؛ چاپ دوم 1925؛ تجدید چاپ، نیویوْرك، 1956)، ص 121، نوشته شده بود. ملكم س. براون، در مأخذ - یاد شده، ص 363-364، و ویلبركنوْر، در The Evolution of Euclideam Elements («تكامل اصول اقلیدسی»، دوْردرخت، 1975)، نیز آن نظریه را تأیید كرده‌اند.
27. طوییقا، ارسطو، هشتم3، 159 A 1-158 B 29.
28. «شرح بر طوییقا»ی اسكندر افروْدیسی، ویراسته‌ی اشتراشه و والیس، در Commentaria in Aristitelem Graece («شرح بر آثار یونانی ارسطو»)، دوم (برلین، 1891)، 12. 545-17.
29. «اصول» اقلیدس، هفتم1، هفتم2، دهم2، و دهم3، ویراسته‌ی ل. هایبرگ، دوم (لایپ تسیش، 1884)، 188. 13-15، 192. 6-7؛ سوم (لایپ تسیش، 1886)، 12-14، 10. 4-5؛ویراسته‌ی ا. س. اشتاماتیس (به پیروی از ی. ل. هایبرگ)، دوم (لایپ تسیش، 1970)، 105. 8-9، 107. 3-4، سوم (لایپ تسیش، 1972)، 3. 19-20، 5. 8-9.
30. ماهانی، شارح عرب (شكوفایی، حدود 860/239)، و به دنبال او نیریزی (شكوفایی، حدود 897/276)، ناخشنود از تعریف اقلیدس، یك تعریف «مطابق ذوق» برای خودش وضع كرد كه مورد توجه ا. ب. پلوئئی واقع شد، اثر مذكور در حاشیه‌ی [26] برای كار نیریزی، - Anaritii in decem libros priores Elementorum Euclidis ex interpretation Gherardi Cremonensis «نیریزی در كتاب دهم اصول اقلیدس به تعبیر ژرار كرموْنایی»)، ویراسته‌ی م. كورتسه، در «مجموعه‌ی آثار اقلیدس»، ویراسته‌ی ی. ل. هایبرگ و هـ. منگه، ضمیمه، ص 157-160.
31. پروْكلوس، اثر مذكور در حاشیه‌ی [7]، ص 67. 20-23؛ ترجمه‌ی انگلیسی، همان اثر، ص 56. 9-12.
32. De Theaeteto Atheniensi Mathematico («درباره‌ی تئایتتوس ریاضیدان آتنی»)، از اوا زاكس، ص 64، به پیروی از اولریش فوْن ویلاموْویتس موْلندوْرف.
كتابشناسی
هیچ نسخه‌ی اصلی از نوشته‌های تئایتتوس، حتی به صورت اقتباس، در دست نیست، اگرچه بدون شك، كارش در «اصول» اقلیدس، دهم و سیزدهم، آمده است.خواندنیهای فرعی مشتملند بر «Theaetetus»، از ج. ج. آلمن، در Hermathena، 6 (1887)، 269-278، تجدید چاپ در Greek Geometry From Thales to Euclid (لندن- دابلین، 1889)، 206-215؛ «Eudoxos Studien I: Eine voreudoxische Proportionenlehre und ihre Spuren bei Aristoteles und Euklid»، از اوْسكار بِكِر، در QSG، 2B (1933)، 311-333؛ همان، 3B (1934)، 533-553، تجدید چاپ در Zur Geschichte der griechischen Mathematik، ویراسته‌ی ا. بِکِر (دارمشتات، 1965)؛ در ABeg، 4 (1959)، 223؛ و در Grundlagen der Mathematik in geschichtlicher Entwicklung (بوْن، 1954؛ چاپ دوم، 1964)، 78-87؛ «Theaetetus: Knowledge as Continued Learning»، از ملكم س. براون، در JHP، 7 (1969)، 359-379؛ «The Discovery of Incommensurability by Hippasus of Metapontum»، از كورت فوْن فریتس، در AMa، 46 (1954)، 242-264؛ «Platon,Theatet und die antike Mathematike»، از همو، در Philo، 87 (1932)، 40-62، 136-178؛ و «The Discovery of Incommensurability by Hippasus of Metapontum»، ویراسته‌ی دیوید ج. فرلی و ر. ا. الن، در Studies in Presocratic Philosophy، یكم (لندن، نیویوْرك، 1970)، 382-412.
نیز - A History of Greek Mathematics، از تامس هیث، یكم (آكسفرد، 1921)، 203-204، 209-212؛ Real-Encyclopedia der classischen Altertums-wissenschaft، از پاولی ویسوْوا، دوره‌ی دوم، پنجم، ستونهای 1351-1372؛ De Theaeteto Atheniensi mathematic از اوا زاكس (رسالهی افتتاحی، برلین، 1914)؛ Die fünf platonischen Körper، از همو (برلین، 1917)، 88-119؛ «Ein Beleg für die voreudoxische Proportionenlehre»، از آرپاد سابوْ، در ABeg، 9 (1964)، 151-171؛ «Die Fruhgeschichte der Theorie der Irrationalitaten»، در Anfänge der griechischen Mathematik، بخش یكم (مونیخ- وین، 1969)، 38-130؛ «Die voreuklidische Proportionlehre»، از همو، همان، بخش 2، صفحات 131-242؛ «Die Entdeckungsgeschichte des Irrationalen nach Plato und anderen Quellen des 4. Jahrhunderts»، از هاینریش فوْكت، در BMat، دوره‌ی سوم، 10 (1909-1910)، 97-155؛ «Zur Entdeckungsgeschichte des Irrationalen»، از همو، همان، 14 (1913-1914)، 9-29؛ Ontwakende Wetenschap، از ب. ل. وان در واردن (خروْنینگن، 1950، به انگلیسی با عنوان Science Awakening، ترجمه‌ی آرنوْلد درسدن (خروْنینگن، 1954، چاپ دوم، [؟]، 1956)، 165-179؛ «Theaetetus and the History of the Theory of Numbers»، از ا. واسرستین، در CQ، 8 (1958)، 165-179؛ «Notes sur l`histoire des mathématiques VIII;Sur la constitution des livres arithmetiques des Eléments d`Euclide et leur rapport à la question de l`irrationalité»، از هـ. گ. تسوْیتن، در DKDVS (1910)، 395-435؛ «Sur les connaissances géométriques ded Grecs avant la reforme platonicienne de la géométrie»، از همو، همان،(1913)، 431-473؛ و «Sur l’origine historique de la connais sance des quantitiés irrationelles»، همان (1915)، 333-362؛ و The Evolution of the Euclidean Elements، از ویلبر كنوْر (دارمشتات، 1975)، فصلهای 7، 8. نیز - كتابشناسی مقاله‌ی تئوْدوْروس كورنه‌ای.
منبع مقاله :
گیلیپسی، چارلز كولستون، (1387)، زندگینامه‌ی علمی دانشوران، ترجمه احمد آرام...[ و دیگران]، تهران: شركت انتشارات علمی و فرهنگی، چاپ اول