

نویسنده: Mario Gliozzi
مترجم: ابوالقاسم قلمسیاه
مترجم: ابوالقاسم قلمسیاه
[evānjelistā torričelli]
Evangelista Torricelli
(ت. فائنتسا، ایتالیا، 23 مهر 987/ 15 اکتبر 1608؛ و، فلورانس، ایتالیا 3 آبان 1026/ 25 اکتبر 1647)، ریاضیات، فیزیک.
تورّیچلّی، که میان سه فرزند گاسپار تورّیچلّی و کاترینا آنجِتّی فرزند ارشد بود، به سرعت استعدادهای خارق العاده از خود نشان داد. پدرش، که بافندهای متوسّط الحال بود، پسر را نزد عمویش یاکوپو (آلسّاندروی سابق) راهب کامالدولی فرستاد تا بر تحصیل او در زبان، ادبیات، و آثار باستانی یونان و روم سرپرستی و نظارت کند. در 1004 و 1005 تورّیچلّی در جلسات درس ریاضیات و فلسفهی مدرسهی یسوعیان در فائنتسا حضور مییافت، و چنان استعداد برجستهای از خود بروز داد که عمویش متقاعد شد که او را برای تحصیل بیشتر به آموزشگاهی که به همت بندتّو کاستِلّی، عضو هم مسلک خودش، و ریاضیدان و مهندس ئیدرولیک و شاگرد پیشین گالیلئو، اداره میشد به رم بفرستد. کاستلّی دلبستگی فراوانی به این جوان پیدا کرد، نبوغ استثنایی او را تشخیص داد، و او را منشی خود ساخت.
مدرک مستقیم ما از دامنه و مسیر مطالعات علمی تورّیچلّی در مدت اقامتش در رم در نخستین نامه (21 شهریور 1011/ 11 سپتامبر 1632) از مکاتبات برجای ماندهی او است که از طرف کاستلّی، که خارج از رم بود، برای گالیلئو فرستاده شد. توْریچلّی، برای اعلام نامهای از گالیلئو به کاستلّی، فرصت را غنیمت شمرده خود را به عنوان ریاضیدانی حرفهای، متبحّری شایسته در هندسهی آپولونیوس، ارشمیدس و تئودوسیوس معرفی کرد؛ او افزود که آثار بطلمیوس را تحصیل کرده است و از طریق آثار برائه، کپلر، و لونگومونتانوس «تقریباً به همه چیز» پی برده است. این مطالعات او را ناگزیر کردهاند که اصول کوپرنیک را بپذیرد «و از لحاظ فرقه و حرفه پیرو گالیلئو» شود؛ او در رم نخستین کسی بود که در کتاب گالیلئو به نام Dialogo sopra i due massimi sistemi («گفتگو دربارهی دو نظام بزرگ»، که در فوریهی همان سال (1632/ بهمن ماه 1010) انتشار یافت مطالعهای دقیق کرده بود.
پس از این نامه تا سال 1031 وقفهای در مکاتبات وجود دارد، و معلوم نیست که تورّیچلّی در آن مدت کجا روزگار میگذرانده یا چه میکرده است. محتملترین فرضی که تاکنون اقامه شده این است که او از بهار 1009 تا بهمن 1019 در دستگاه عالیجناب جووانّی چامپولی، دوست و حامی گالیلئو، که از 1011 فرماندار شهرهای مختلف در مارکِس و اومبریا (مونتالتو، نورچا، سان سِوِرینو فابریانو) بود، منشیگری میکرد؛ تورّیچلّی بار دیگر در 1020در رم بود. او عقاید كاستلّى و ریاضیدانان دیگر را دربارهی رسالهای راجع به حرکت جویا شده بود که آموزهی حرکت پرتابهها را، که گالیلئو در سومین روز از Discorsi e dimostrazioni matematiche introno a due nuove scienze... («گفتارها و برهانهای ریاضی درباره دو علم جدید»، لیدن، 1638) بتفصیل بیان کرده بود، شرح و بسط میداد. کاستلّی این اثر را بسیار عالی میدانست؛ درباره آن با گالیلئو گفتگو نمود؛ و در فروردین پس از آن که تورّیچلّی را برگماشت تا در غیاب او تدریس کند، در راه سفرش از رم به ونیز از مسیر پیسا و فلورانس، دستنویسی را به گالیلئو تسلیم نمود، و پیشنهاد کرد که در تهیه و تنظیم دو «روز» که او فکر کرده است بعداً به «گفتارها...» اضافه کند تورّیچلّی را به عنوان دستیار بپذیرد. گالیلئو موافقت کرد و از تورّیچلّی دعوت نمود که در آرچتری به او ملحق شود.
ولی تاخیر کاستلّی در بازگشت به رم و مرگ مادر تورّیچلّی، که با فرزندان دیگرش به رم نقل مکان کرده بود، تورّیچلّی را ناگزیر کرد که ورود خود به آرچتری را تا 19 مهر 1020 به تعویق اندازد. او در خانهی گالیلئو، که قبلاً وینچنتسو ویویانی در آن زندگی میکرد، اقامت گزید، و تا زمان مرگ گالیلئو که در 19 دی 1020 فرارسید در دوستی نزدیک با او در آنجا ماند. در حالی که تورّیچلّی آماده بازگشتن به رم بود، فردیناندوی دوم، دوک بزرگ توسکانی، به پیشنهاد آندرئا آرّیگتّی، او را به مقام ریاضیدان و فیلسوف منصوب کرد، مقامی، با حقوق خوب و اقامت در کاخ مدیچی، که در اثر مرگ گالیلئو بیمتصدی مانده بود.
تورّیچلّی تا آخر عمر در فلورانس ماند. این سالها، یعنی خوشترین سالهای زندگی او، سرشار از بزرگترین فعالیت علمی بودند. دیری نکشید که وی، که در اثر طرز بیان آراسته و درخشان و لطیفه دارش احترام بسیار کسب کرد، با نمایندگان برجستهی فرهنگ فلورانسی-سالواتوره روزای نقاش، کارلوداتی آگاه از فرهنگ و ادب یونانی، و آندرئا آزیگتّیِ مهندس ئیدرولیک-طرح دوستی ریخت. در واقع، جلسات منظم با این دوستان سبب پیدایش «فرهنگستان پرکوسی» شد، که تورّیچلّی ظاهراً از کمدیهائی که مینوشت ایشان را باخبر میکرد؛ این کمدیها پس از مرگ او باقی نماندهاند ولی در خاطراتی که در بستر مرگش برای لودوویکو سرنایی دیکته کرد صریحاً ذکر شدهاند («مجموعه آثار»، چهارم، 88).
در سال 1023 تنها اثری که از تورّیچلّی در مدت زندگیش بچاپ رسید و دوک بزرگ تمام مخارج چاپ آن را متقبل شده بود، انتشار یافت. مجلّد Opera geometeica («آثار هندسی») به سه بخش تقسیم شده بود: بخش یکم مربوط میشد بهdu De Sphaera et solidis Sphaeralibus libri؛ بخش دوم مشتمل بود بر De motu gravium naturaliter descendentium et proiectorum (این نوشته به گالیلئو به پاس عقیدهاش تقدیم شد)؛ و بخش سوم عبارت بود از De dimemsione parabolae. این اثر، که در اندک زمانی در سراسر ایتالیا و اروپا شهرت یافت، ارزش ذاتی داشت، و بیان واضحش موجب شد که هندسهی کاوالیئری، که خواندن نوشتههایش دشوار بود، اشاعه یابد.
شهرتی که تورّیچلّی به عنوان هندسه دان کسب کرد سبب افزایش مکاتبات او با دانشمندان ایتالیایی و تعدادی از دانشمندان فرانسه [کارکاوی، مِرسِن، ف. دو وِردو، روبروال] شد که توسط ف. نیسرون، که هنگام اقامت در رم وی را ملاقات کرده بود، به آنان معرفی شد. این مکاتبات وسیلهی ابلاغ و انتقال بزرگترین کشفیات علمی تورّیچلّی و همچنین موجبی برای مباحثات شدید درباره حقّ تقدّم بودند، که در طول آن قرن جریان داشت. این مباحثات، مخصوصاً با روبروال دربارهی حقّ تقدّم کشف بعضی از خواص چرخزاد (cycloid)، از جمله تربیع، گرانیگاه، و اندازه گیری حجم حاصل از دَوَران آن حول قاعده، مشاجرات قلمی جدّیای بودند. توَرّیچلّی، برای دفاع از حقوق خود، تصمیم گرفت که تمام مکاتبات خود با ریاضیدانان فرانسوی را منتشر کند، و در 1025 شروع کرد به پیش نویسی اثری به نام Racconto d"alcuni problemi proposti e passati tra gli matematici di Francia et il Torricelli ne i quattro anni prossimamente passati («مجموعهی آثار»، سوم، 1-32). ولی هنگامی که به این کار مشغول بود به سبب ابتلا به بیماری شدیدی (احتمالاً تب حصبه)، که فقط چند روز به طول انجامید، وفات یافت. بنابر وصیّتش در کلیسای سان لورنتسو در فلورانس به خاک سپرده شد، ولی محلّ قبرش معلوم نیست.
توْرّیچلّی در تمام عمر به تحقیق در ریاضیات مشغول بود. در دوران جوانی آثار قدیمی و معتبر هندسهی یونانی را، که با روش حذف تصاعدی به مسائل مربوط به بینهایت کوچکها میپرداختند، فراگرفت. ولی از آغاز قرن هفدهم روش کلاسیک تا حدی جای خود را به فرایندهای شهودیتر داده بود؛ نخستین مثالها را کپلر بدست داد، که برای تعیین سطحها و حجمها از روشهای ارشمیدس دست برداشت و به شیوههای سریعتری روی آورد که از مسألهای تا مسأله دیگر فرق میکردند و به همین سبب بدشواری قابل تقلید بودند. کاوالیئری، پس از چندین سال تفکر، در هندسه بخش ناپذیرهای خود (1014)، به یک فرایند اساسی توجه کرد که روبرال، فرما، و دکارت هم تقریباً در همان سال در جهت آن حرکت کرده بودند؛ این تصادف نشان میدهد که زمان برای رویکردهای هندسی جدید فرارسیده بود.
هندسهی جدید هر شکل مسطح را متشکل از بینهایت تار در نظر میگرفت که به وسیلهی یک رشته خطوط مستقیم متوازی در داخل شکل جدا میشدند: سپس هر تار همچون مستطیل بینهایت باریکی انگاشته میشد که، بر طبق اصطلاحی که گالیلئو باب کرد، «بخش ناپذیر» نامیده میشد. از روابط مفروض یا محقق بین بخش ناپذیرها امکان استنتاج روابط بین مجموعها از طریق اصل کاوالیئری وجود داشت، که میتوان آن را چنین بیان نمود: دو شکل مسطح تقسیم شده بین خطوط مستقیم متوازی مفروض است؛ اگر همهی این خطوط مستقیم متوازی پارهخطهائی را در دو شکل مشخص سازند که رابطهی ثابتی داشته باشند، آنگاه مساحتهای دو شکل نیز همان رابطه را دارند. این اصل بآسانی به شکلهای فضایی بسط داده میشود. اصولاً هندسه کاوالیئری نخستین گام به سوی حساب بینهایت کوچکها بود، که به جای بینهایت بزرگ و بینهایت کوچکی ریاضی بالقوه هندسه دانان یونانی بینهایت بزرگ و بینهایت کوچکی حاضر را قرار داد.
تورّیچلّی، پس از تسلّط بر بیاعتمادی اولیه خود به روش نوین، از آن به عنوان ابزاری ابتکاری برای کشف قضایای جدیدی استفاده کرد که بعداً با روشهای قدیمی معتبر آنها را مدلل میکرد. کاربرد مختلط دو روش-یعنی روش بخش ناپذیرها برای کشف کردن و طریقهی ارشمیدس برای ثابت کردن-در کتاب «آثار هندسی» فراوان است. بخش یکم De Sphaera et solidis Sphaeralibus، که در حدود سال 1020 تألیف شده است، شکلهای حاصل از دوران یک چند ضلعی منتظم محاط در دایره یا محیط بر آن حول یکی از محورهای تقارن را (که قبلاً توسط ارشمیدس بیان شده بود) مورد بررسی قرار میدهد. تورّیچلّی مشاهده میکند که اگر چند ضلعی منتظم دارای اضلاع متساوی باشد، یکی از محورهای تقارنش دو رأس متقابل یا وسط دو ضلع متقابل را به هم وصل میکند؛ از طرف دیگر، اگر اضلاع آن مساوی نباشند، یکی از محورهای تقارنش یک رأس را به نقطه وسط ضلع مقابل وصل مینماید. او، براساس این مشاهده، احجام حاصل از چنین دَوَران را به شش قسم طبقه بندی میکند، خواص آنها را بررسی مینماید، و قضیههای جدید و روابط متریِ جدیدی برای اجسام گِرد (مدوّر) هندسهی مقدماتی عرضه میدارد. در بخش دوم کتاب، حرکت پرتابهها مورد بحث قرار میگیرد.
در بخش سوم، قطع نظر از درج بیست برهان برای قضیهی ارشمیدس دربارهی تربیع سهمی بدون اضافه کردن چیز تازهی مهمی به آن، تورّیچلّی نشان میدهد که سطح محصور بین چرخزاد و قاعدهاش مساوی سه برابر سطح دایرهی مولد آن است. به عنوان ضمیمهای بر این بخش از کار، پژوهشی دربارهی حجم حاصل از حرکت حلزونی شکل یک سطح مستوی بر گِرد محوری از صفحهاش وجود دارد، با اثبات این نکته که این حجم مساوی با حجم حاصل از دَوَران کامل آن سطح به گرد همان محور است. تورّیچلّی این قضیه ظریف را در مسائل متعدد بکار میبرد، بویژه برای رویه یک پیچ با رزوهای تخت که او مساوی بودن آن را با قسمت مناسبی از یک سهمیگون دارای یک گام نشان میدهد.
تورّیچلّی، همین که آشنایی فزایندهای با روشی بخش ناپذیرها پیدا کرد.-به گفتهی خود کاوالیئری-به نقطهی فوق استادی و مهارت رسید. در واقع او این نظریه را با استفاده از بخش ناپذیرهای منحنی، بر پایهی مفهوم اساسی زیر، بسط داد: برای مقایسه کردن دو شکل مسطح، اولی با مجموعی از منحنیها و دومی با مجموعی از خطوط مستقیم موازی تقسیم میشود: اگر هر بخش ناپذیر منحنی در اولی مساوی با بخشی ناپذیر متناظر در دومی باشد، مساحتهای دو شکل باهم برابرند. سادهترین مثال، مقایسهی یک دایرهی تقسیم شده به حلقههای هم مرکز بینهایت کوچک است با مثلثی تقسیم شده به تارهای بینهایت کوچک موازی با قاعده (قاعدهی این مثلث محیط دایره است که به صورت خط راست درآمده و ارتفاع مثلث شعاع آن دایره است). از تساوی حلقهها با نوارهای متناظر نتیجه میشود که مساحت دایره با مساحت مثلث برابر است.
این اصل به شکلهای فضایی نیز بسط داده شده است. تورّیچلّی درخشانترین کاربرد آن را در 1020 با اثبات قضیهای جدید، که گوهری در نوشتههای ریاضی زمان است، بدست داد. این قضیه، که در «آثار هندسی» منتشر شد، به شرح زیر است («مجموعهی آثار»، یکم، 191-213): نقطهای روی یک هذلولی متساوی الساقین (به معادلهی 1=xy) فرض کنید و سطحی را در نظر بگیرید که از مقطع نامحدود هذلولی دارای مجانب x، مجانب x، و عرض نقطهی انتخاب شده تشکیل شده باشد. اگرچه چنین سطحی از لحاظ اندازه نامتناهی است، جسمی که در اثر دَوَران این سطح حول مجانب به وجود میآید، هرچند از حیث وسعت نامحدود است، با وجود این دارای حجم محدودی است، که بر طبق محاسبه تورّیچلّی
 است، و a در آن طول نقطه مفروض در روی هذلولی است.
است، و a در آن طول نقطه مفروض در روی هذلولی است.
برهان تورّیچلّی، که کاوالیئری آن را بسیار ستوده و فرما از آن تقلید کرده است، متضمن این فرض است که جسم حاصل از دوران مرکب است از تعداد بینهایت سطوح استوانهای شکل با محور، که همه آنها دارای مساحت جانبی مساوی هستند، همهی آنها در تناظر دو سویه با مقاطع یک استوانه مناسب قرار دارند، و همهی آنها مساوی با سطوح آن استوانهاند: اصل بخش ناپذیرهای منحنی این نتیجه را میدهد که حجم این استوانه مساوی با حجم جسمی است که از دَوَران مقطع هذلولی موردنظر ایجاد میشود. برطبق اصطلاحات جدید، روش کار تورّیچلّی با بیان این نکته توصیف میشود که هر انتگرالی در دستگاه مختصّات دکارتی جای خود را به انتگرالی در دستگاه مختصات استوانهای میدهد. تورّیچلّی، بازهم با استفاده از بخش ناپذیرهای منحنی، در میان کارهای دیگرش، حجم جسم محدود به دو سطح مستوی و هرگونه سطح جانبی، بویژه حجم بشکهها، را پیدا کرد. در 1022 نتایج برای فرما، و دکارت و روبروال فرستاده شد، و آنان آنها را بسیار دقیق و درست یافتند.
مورد هذلولی تورّیچلّی را وادار کرد که منحنیهای کلیتری را مطالعه کند که امروزه با معادلاتی که صورت دارند تعریف میشوند؛ در این معادلات m و n اعداد درست مثبت و n≠ m است. وی کشف کرد که دَوَران این منحنیها حول یک مجانب ممکن است جسمی بینهایت دراز با حجم محدود ایجاد کند و، در شرایطی خاص، سطح محصور بین مجانب و منحنی نیز ممکن است محدود باشد. تورّیچلّی تصمیم گرفت که همهی این نتایج را موزون و هماهنگ کند؛ در سالهای 1025 و 1026 نتایج را در یک اثر فردی با عنوان De infinitis hyperbolis («هذلولیهای نامحدود») با نامه به ریاضیدانان متعدد ابلاغ کرد، ولی پیش از آن که بتواند آن را کامل کند وفات یافت. تنها پس از انتشار «مجموعه آثار» این امکان فراهم آمد که این مقاله از روی یاداشتهای پراکنده بازنویسی شود.
دارند تعریف میشوند؛ در این معادلات m و n اعداد درست مثبت و n≠ m است. وی کشف کرد که دَوَران این منحنیها حول یک مجانب ممکن است جسمی بینهایت دراز با حجم محدود ایجاد کند و، در شرایطی خاص، سطح محصور بین مجانب و منحنی نیز ممکن است محدود باشد. تورّیچلّی تصمیم گرفت که همهی این نتایج را موزون و هماهنگ کند؛ در سالهای 1025 و 1026 نتایج را در یک اثر فردی با عنوان De infinitis hyperbolis («هذلولیهای نامحدود») با نامه به ریاضیدانان متعدد ابلاغ کرد، ولی پیش از آن که بتواند آن را کامل کند وفات یافت. تنها پس از انتشار «مجموعه آثار» این امکان فراهم آمد که این مقاله از روی یاداشتهای پراکنده بازنویسی شود.
هندسهی بخش ناپذیرها را تورّیچلّی در تعیین گرانیگاه شکلها نیز بکار برد. در نامهای به تاریخ 18 فروردین 1025 به میکلانجلو ریتچی، او «قضیهی کلی» را، که حتی امروز هم جامعترین قضیه ممکن انگاشته میشود، فاش ساخت، قضیهای که تعیین گرانیگاه هر شکل را از راه رابطه بین دو انتگرال میسر میسازد. از میان حالات خاص، باید اشاره به تعیین گرانیگاه قطاع مستدیری کرد که هم به طریقهی قدیمی و مرسوم و هم با روش بخش ناپذیرها بدست آمد. تورّیچلّی به همان نتیجهای رسید، و شاید هم میدانست، که شارل دو/ لافای در 1011 به آن رسیده بود.
تورّیچلّی توجه خود را به تعیین طول قوسهای یک منحنی نیز معطوف کرد، کاری که دکارت، پس از آن که از طریق مِرسِن اطلاع یافت که روبروال تساوی طول قوسهای خاصی از سهمی و طول قوسهای مارپیچ ارشمیدس را اثبات کرده است، در رساله یGéométrie («هندسه»، 1637) غیرممکن بودن آن را اعلام کرد. تورّیچلّی، با تصور «مارپیچ لوگاریتمی»، که آن را «هندسی» مینامید، روشی را آموخت که تعیین طول تمام قطعه واقع بین هر نقطه از منحنی و مرکز را، که منحنی پس از تعداد بینهایت دَوَران به آن میرسد، با خطکشی و پرگار میسر میکرد. علاوه بر این، او ثابت کرد که هر مارپیچ ارشمیدس-یا، بنا به گفتهی خود او، (مارپیچ حسابی»-را همواره میتوان با هر قوسی خاصی از یک منحنی سهمیگون مناسب مساوی ساخت.
تورّیچلّی، علاوه بر این خدماتی که به حساب انتگرال کرد، به تعدادی از روابط حساب دیفرانسیئل نیز پی برد. در میان بهرههائی که وی از مفهوم مشتق، مأخوذ از آموزه حرکت، گرفت (-پایین)، بجا است که ذکری از تحقیق وی دربارهی بیشینهها و کمینههاminima) ، (maxima به میان آید. او نشان داد که اگر مجموع x+y ثابت باشد، حاصل ضرب در صورتی بیشینه است که x و y در حالت نمایی همان را داشته باشند. وی همچنین نقطهای را که هنوز هم به نقطه تورّیچلّی معروف است روی سطح مثلثی معیّن کرد، که مجموع فواصل آن از رئوس مثلث کمینه است؛ این مسأله را فرما مطرح کرده بود.
در صورتی بیشینه است که x و y در حالت نمایی همان را داشته باشند. وی همچنین نقطهای را که هنوز هم به نقطه تورّیچلّی معروف است روی سطح مثلثی معیّن کرد، که مجموع فواصل آن از رئوس مثلث کمینه است؛ این مسأله را فرما مطرح کرده بود.
تورّیچلّی، ضمن مطالعاتش در زمینه مکانیک، خدمات مهم دیگری هم به ریاضیات کرد. در رسالهی De motu gravium، وی بررسی حرکت سهمیگون پرتابهها را، که گالیلئو آغازگر آن بود، ادامه داد، و مشاهده کرد که اگر نیروی شتابگر در هر نقطه از مسیر حذف شود، پرتابه در راستای مماسی بر مسیر حرکت خواهد کرد. او این مشاهدات را، که موجب تحسین گالیلئو بودند، برای رسم مماس بر نقطهای از مارپیچ ارشمیدس، یا چرخزاد، مورد استفاده قرار داد، با در نظر گرفتن این که منحنیها به وسیله نقطهای که دارای دو حرکت همزمان است رسم شوند. این موضوع در یادداشتهای انتشار نیافته به گونهای کاملاً جامعتر بررسی شده است. نقطهای در نظر گرفته شده است که دارای دو حرکت همزمان، یکی یکنواخت و دیگری متغیر، در امتداد دو خط راست عمود برهم است. تورّیچلّی، پس از ترسیم منحنی مسافت به عنوان تابع زمان، نشان میدهد که خط مماس بر هر نقطه از منحنی با محور زمان زاویهای میسازد که تانژانت آن اندازه سرعت جسم متحرک در آن نقطه را بدست میدهد. اصولاً این موضوع تأییدی است بر این که عملیات انتگرال گیری و مشتق گیری سرشتی عکس یکدیگر دارند. این نکته قضیه اساسی حساب جامع و فاضلی را تشکیل میدهند که آیزک بَرو آن را در 1049 انتشار داد، و از میان پیشینیانش از گالیلئو، کاوالیئری، و تورّیچلّی نام برد. ولی حتی برو هم اهمیت قضیه را، که نخستین بار به همّت نیوتن به اثبات رسید، درک نکرد.
برتری کامل روشهای هندسی جدید تورّیچلّی را از خطرهای ذاتی آگاه ساخت، به طوری که دستنویسهای او حاوی مطالبی بر ضد بینهایتها است. نوشتههای انتشار نیافتهی وی، در واقع، مجموعهای از باطلنما (پارادوکس)هائی را در بر دارند که آموزه بخش ناپذیرها، اگر با احتیاطهای لازم بکار برده نشوند، به آنها میانجامند.
تورّیچلّی در De motu grauium درصدد است که اصل گالیلئو دربارهی تساوی سرعتهای سقوط آزاد وزنهها در امتداد سطحهای شیبدار با ارتفاع مساوی را به اثبات رساند. او اثبات خود را بر پایه اصل دیگری بنا میکند که اکنون اصل تورّیچلّی نامیده میشود ولی بر گالیلئو معلوم بود؛ بر طبق این اصل، دستگاهی صُلب مرکب از تعدادی جسم فقط در صورتی میتواند به خودی خود بر سطح زمین حرکت کند که گرانیگاه آن پایین برود. تورّیچلّی، پس از بکار بستن این اصل در حرکت بر روی وترهای دایره و سهمی، به حرکت پرتابهها روی میآورد و، با تعمیم دادن آموزه گالیلئو، پرتاب تحت هر زاویه مایل را در نظر میگیرد- در صورتی که گالیلئو فقط پرتاب افقی را منظور داشته بود. او مشاهده اتفاقی گالیلئو را به صورتی کلی اثبات میکند که اگر پرتابهای در هر نقطه از مسیر با سرعتی مساوی با سرعت مکتسب در آن نقطه در جهت مخالف از نو پرتاب شود، همان مسیر را در جهت معکوس خواهد پیمود. این گزاره هم ارز است با این گفته که پدیدههای دینامیکی برگشت پذیرند- یعنی زمانِ مطرح شده در مکانیک گالیلئو ترتیب دارد اما فاقد جهت است. تورّیچلّی، در زمرهی تعدادی از قضایای علم پرتابههای خارجی، نشان داد که سهمیهای متناظر با سرعت اولیهی معین و متناظر با میلهای متفاوت، همه بر سهمی واحدی مماسند (معروف به سهمی ایمنی یا سهمی تورّیچلّی، که نخستین مثال از منحنی پوش دستهای از منحنیها است).
رساله با پنج جدول عددی به پایان میرسد. چهار جدول اول آن جدول مثلثاتی هستند که بترتیب مقادیر ، را برای هر یک از درجههای بین
، را برای هر یک از درجههای بین  و
و  بدست میدهند؛ با این جدولها، وقتی که سرعت اولیه و زاویهی پرتاب معیّن باشند، بقیهی اجزای مشخصهی مسیر را میتوان حساب کرد. جدول پنجم زاویهی پرتاب را، وقتی که فاصلهی فرود گلوله و بیشینه برد اسلحه معلوم باشند، بدست میدهد. در تحلیل نهایی، اینها جداول پرتاب گلوله توپ هستند، که ارزش عملی آنها به سبب شرح کاربردشان به زبان ایتالیایی، که درکش برای توپچیان آسانتر از لاتینی است، بیشتر میشود. زبان ایتالیایی همچنین در شرح پایانی جدول جدیدی بکار رفته است و این امر محاسبه ارتفاع اسلحه را برای افسران توپخانه آسان میسازد.
بدست میدهند؛ با این جدولها، وقتی که سرعت اولیه و زاویهی پرتاب معیّن باشند، بقیهی اجزای مشخصهی مسیر را میتوان حساب کرد. جدول پنجم زاویهی پرتاب را، وقتی که فاصلهی فرود گلوله و بیشینه برد اسلحه معلوم باشند، بدست میدهد. در تحلیل نهایی، اینها جداول پرتاب گلوله توپ هستند، که ارزش عملی آنها به سبب شرح کاربردشان به زبان ایتالیایی، که درکش برای توپچیان آسانتر از لاتینی است، بیشتر میشود. زبان ایتالیایی همچنین در شرح پایانی جدول جدیدی بکار رفته است و این امر محاسبه ارتفاع اسلحه را برای افسران توپخانه آسان میسازد.
در یک بند از رساله به حرکت آب نیز با چنان اهمیتی اشاره شده است که ارنست ماخ تورّیچلّی را بنیاد گذار ئیدرودینامیک اعلام کرد. هدف تورّیچلّی این بود که سرعت ریزش مایعی را که از سوراخ کوچک ته ظرفی بیرون میریزد معین کند. او به کمک آزمایش متوجه شده بود که هرگاه مایع رو به بالا فوران میکرد، فواره به ارتفاعی میرسید که پایینتر از سطح مایع در ظرف بود. بنابراین، فرض کرد که اگر همهی مقاومتها در مقابل حرکت به صفر برسند، فواره به سطح مایع خواهد رسید. از این فرضیه، که هم ارز اصل بقا است، قضیهای را استنتاج کرد که نام او را بر خود دارد: سرعت فوران مایع در نقطه خروج برابر با سرعتی است که یک قطره میداشت اگر میتوانست از سطح آزاد مایع بالای سوراخ در خلاً به طور آزاد سقوط کند. تورّیچلّی همچنین نشان داد که اگر سوراخ در جدار ظرف ایجاد شود، مسیر فوران مایع به شکل سهمی خواهد بود؛ سپس آن بند از رساله را با مشاهدات جالب توجه دربارهی از هم پاشیدن جریان مایع به صورت قطرهها و دربارهی اثرهای مقاومت هوا به پایان رسانید. مهارت تورّیچلّی در علم ئیدرولیک برای همعصرانش چنان بخوبی شناخته شد که دربارهی پاکسازی درهی رود کیانا از آبهای راکد با او مشورت کردند، و او روش خاکریزی را برای احیای آن پیشنهاد کرد.
تبدیل «دما بین» (ترموسکوپ) گازیِ ابتداییِ گالیلئو به دماسنج (ترمومترِ) مایعی، که نخست با آب و بعد با الکل پرشد، اغلب به توْرّیچلّی نسبت داده شده، اگرچه گاهی هم فکر آن از دوک بزرگ فردیناندوی دوم دانسته شده است. از طرف دیگر، مدرک بسیار خوبی از توانایی فنی او در ساخت عدسیهای تلسکوپ وجود دارد، مهارتی که به احتمال قریب به یقین در مدت اقامتش در فلورانس آن را کسب کرده بود. او تا پاییز 1021 توانایی ساختن عدسیهای نسبتاً خوبی را بدست آورده بود، هرچند به پای عدسیهای عالیای که فرانچسکو فوانتانا، نامدارترین تلسکوپساز ایتالیایی آن زمان، میساخت نمیرسیدند. تورّیچلّی دست به کار شده بود تا با فونتانا رقابت کند و از او پیش افتد. تا 1022 توانست عدسیهائی مانند عدسیهای فونتانا، حتی شاید بهتر، تهیه کند، ولی بالاتر از همه متوجه شد که آنچه در واقع برای کارایی یک عدسی اهمیت دارد تراش کاملاً کروی سطح آن است، که وی با فنون ظریف انجام میداد. کارایی عدسیهای تورّیچلّی را دوک بزرگ تأیید کرد، و در 1023 به توْریچلّی گردن بندی طلا حامل ایک مدال با عبارت «Virtutis praemia» اهدا کرد.
شهرت عدسیهای عالی تورّیچلّی بسرعت همه جا منتشر شد و او سفارشهای زیاد دریافت میکرد و ثروت خوبی بدست آورد. وی کارایی تلسکوپهای مجهز به عدسیهایش را به طریقهی تراشی نسبت میداد که در آن زمان به صورت راز نگهداشته شد، ولی در برخی از مقالات توصیف گردید که پس از مرگ تورّیچلّی به دوک بزرگ انتقال یافتند، و او آنها را به ویویانی سپرد، که بعد از آن گم شدند. گاهی داستان ماهرانهای درباره این «راز» ساخته شده است؛ ولی بازسازی کامل «راز» تورّیچلّی از مدرکهای برجا مانده ممکن به نظر میرسد- که، قطع نظر از نیاز به بالابردن شایستگیهای محصول کارش در نظر دوک بزرگ، عمدتاً عبارت بودند از تراش و پرداخت بسیار دقیق سطوح، انتخاب شیشهی مرغوب، و محکم نکردن عدسیها «با زِفت یا به هر طریق با آتش». ولی این احتیاط آخری که، بنا به گفته تورّیچلّی، فقط خدا و خودش از آن خبر داشتند- از طرف هیئرونیموس سیرتوری در Telescopium او از 997 توصیه شده بود. در هر حال، یکی از عدسیهای تلسکوپی تورّیچلّی، که اکنون همراه با یادگارهای دیگر در «موزهی سرگذشت علم» در فلورانس نگهداری میشود، در 1303 توسط واسکو روانکی با استفاده از توری پراش معاینه شد. معلوم شد که کیفیت ساخت آن چندان استادانه و عالی است که یک وجه آن ظاهراً بهتر از آیینهای که عنوان سطح مرجع را داشت تراشیده و پرداخت شده، و با پیشرفتهترین شیوهی آن دوره ساخته شده است.
سخنرانیهائی که تورّیچلّی به مناسبتهای مختلف ایراد کرد، و توماسو بوناونتوری آنها را در کتابی با عنوان Lezioni accademiche («دروس فرهنگستانی») گرد آورد که پس از درگذشت وی انتشار یافت، مرجّحاً درباره موضوعات فیزیکی بودند. آنها عبارتند از هشت سخنرانی در فرهنگستان کروسکا، که وی یکی از اعضای آن بود (یک سخنرانی برای سپاسگزاری به مناسبت پذیرفته شدن در فرهنگستان، سه تا درباره نیروی برخورد، دو تا دربارهی سُبکی، یکی راجع به باد، و یکی دربارهی شهرت)؛ یک سخنرانی در ستایش ریاضیات، که در کارگاه هنری فلورانس ایراد شد؛ دو سخنرانی دربارهی معماری نظامی در فرهنگستان نقشه کشی؛ و یکی در ستایش از «قرن طلایی»، عصر افسانهای کمال انسانی، که در «فرهنگستان پرکوسّی» ایراد شد.
سخنرانیهای مربوط به نیروی برخورد و دربارهی باد، از دیدگاه علم فیزیک، از جاذبه و اهمیت خاصی برخوردارند. وی در اولی گفت که گزارش دهندهی عقایدی است که گالیلئو در گفتگوهای غیررسمی آنان ابراز کرده است، و در آن مشاهدات و آرای اصیل و ابتکاری وجود دارد. به عنوان مثال، مکسول این ادعا را که «نیروها و قوهی حرکت» (چیزی که آن را کارمایه [انرژی] مینامیم) در اجسام نهفتهاند در آخرین بند ازTreatise on Electricity and magnetism («رساله دربارهی برق و مغناطیس»، 1873) بدین معنی تعبیر کرده است که انتشار کارمایه یک عمل با واسطه است نه عملی از دور، تورّیچلّی، در سخنرانی راجع به باد، نظریهی رایج تشکیل باد را رد کرد؛ بر طبق آن عقیده، باد ناشی از بازدمهای بخارداری بود که از زمین مرطوب ایجاد میشد؛ از طرف دیگر، این نظریه جدید را مطرح کرد که بادها در اثر اختلاف دمای هوا، و در نتیجه اختلاف چگالی، بین دو ناحیهی زمین ایجاد میشوند.
ولی، بالاتر از همه، نام تورّیچلّی با آزمایشی برای سنجیدن فشار هوا پیوسته است که به نام او خوانده میشود. بحث درباره خلا یا پری (ملأ) تا نخستین مکاتب فلسفی یونان به عقب برمیگردد. در قرون وسطی، الهیات کاتولیکی آموزه ارسطو را که خلاً تناقضی است در منطق کنار زد و این مفهوم را به جای آن نشاند که طبیعت از خلاً نفرت دارد (امتناع از خلأ، horror vacui). در دورهی رنسانس بحث بین طرفداران خلأ و طرفداران ملأ دوباره بالا گرفت، گالیلئو، با پیوستن به تلزیو و برونو، فلاسفهی خردگرا، با استدلالهای ارسطو درباره خلأ به مخالفت برخاست و در حدود سال 992 وزن داشتن هوا را با آزمایش اثبات کرد. ولی، همانند اکثریت همعصران خود، معتقد بود که هیچ عنصری به خودی خود دارای وزن نیست؛ از این رو بر پایهی وزن معیّن شدهی هوا، نمیتوانست فشارهای درون هوای جوّ را استنتاج کند. برای توضیح این پدیده که آب در تلمبههای مکنده بیش از هجده «براتچا» (braccia، تقریباً نه متر) بالا نمیآید، چنان که چاه کنان فلورانسی مشاهده کرده بودند، گالیلئو فرضیهی یک نیرو-«نیروی خلأ»- را مطرح کرد که درون تلمبه یافت میشد و میتوانست تعادل ستونی از آب به ارتفاع هجده براتچا را حفظ کند.
در 1009، هنگامی که جووانّی باتّیستا بالیانی از وی پرسید که چرا سیفونی که از روی تپهای به ارتفاع حدود بیست و یک متر گذشته است کار نمیکند، گالیلئو در پاسخ چند بار نظریهاش دربارهی نیروی خلأ را تکرار کرد. بالیانی با ردّ پاسخ گفت که به عقیده وی کار نکردن سیفون ناشی از وزن هوا است که، با فشار آوردن به همهی اطراف، ستون آبی را نگه میدارد که در قسمت بالای سیفون تحت فشار نیست، و هوای سیفون هم در اثر جریان آبی که آن را پر میکند خارج شده است. ولی گالیلئو عقاید بالیانی را نپذیرفت، و در «گفتارها» (1638) همچنان به حمایت از نظریه «نیروی خلأ» ادامه داد. پس از مرگ گالیلئو بحث بین پیروانش در رم و فلورانسی ادامه یافت؛ و محتمل است که پیروانش در رم به تورّیچلّی روی آورده باشند تا عقیده او را درباره طرز کار تلمبههای مکنده یا درباره آزمایش مشابهی جویا شوند که گفته میشود گاسپارو برتی در 1019 در رم انجام داده است تا نشان دهد که آب در تلمبههای مکنده بیش از هجده براتچا بالا میرود.
تورّیچلّی، که شاید با تصور بالیانی آشنا بود، به تکرار آزمایش برتی یا بالیانی پرداخت؛ و در آن از مایعهای رفته رفته سنگینتر مانند آب دریا، عسل، و جیوه، که در توسکانی استخراج میشد، استفاده کرد. استفاده از جیوه همچنین به او امکان داد که، با قرار دادن یک لولهی شیشهای سادهی تقریباً یک متری به جای سیفون بالیانی یا برتی، عمل پرکردن را آسان کند. او طرح ریزی کرد که لوله را تا لبه آن از جیوه پرکند، دهانهی آن را با انگشت ببندد و آن را وارونه سازد، و دهانه باز آن را در جیوه درون کاسهای فرو برد. ساختن چنین لولهی درازی که بتواند وزن جیوه را تحمل کند در آن زمان کار آسانی نبود (فقط در 1025 مرسِن توانست لوله به قدر کافی محکمی از کارخانه شیشه سازی فرانسه تهیه کند)؛ تورّیچلّی از ویویانی خواست که یکی برایش بسازد، و به این ترتیب ویویانی نخستین کسی بود که آزمایش را انجام داد.
توْرّیچلّی، در نامهای به تاریخ 22 خرداد 1023 به میکلانجلو ریتچی، آزمایش را شرح داد و، با رد کردن نظریهی نیروی خلأ آن را مطابق گفته بالیانی تفسیر کرد. اما وی حتی پیش از انجام دادن آزمایش از تغییرات فشار جو اطلاع داشت، زیرا در نامهاش متذکر میشود که «می خواست اسبابی بسازد که تغییرات هوا را نشان دهد: یک زمان سنگینتر و چگالتر، یک زمان سبکتر و رقیقتر. برطبق فرضیهای نسبتاً مستند و اساسی، او ضمن مشاهده استادانهی رفتار اسباب بازیهای ئیدروستاتیکی، که شاید توسط خود او اختراع شده و بعداً «شیطانکهای دکارتی» نامیده شدند، اطلاعاتی دربارهی فشار جو بدست آورده بود. به گفته تورّیچلّی، نیروئی که ستون جیوه را نگه میدارد نیروی درون لوله تا بلکه نیروی خارجی حاصل از جو است که وزن آن بر جیوه درون کاسه نیرو وارد میکند. اگر به جای جیوه، لوله حاوی آب باشد، ارتفاع ستون آب، بر طبق پیش بینی تورّیچلّی، به نسبت فزونی سنگینی جیوه بیشتر خواهد بود، و این نتیجهای بود که در 1026 توسط پاسکال به اثبات رسید. در تأیید این فرضیه که علّت نگه داشته شدن جیوه [در لوله] امری است خارجی نه داخلی، تورّیچلّی به شرح آزمایشهای دیگری با لولهها میپردازد که، با دمیدن در یک کره از بالای آن، ستونهای جیوه به ارتفاعهای مساوی در لولهها بدست میآمدند، به طوری که نیرو از حجم خلاً ناشی نمیشد و بنابراین «نیروی خلأ» در میان نبود.
ریتچی، در پاسخ خود به نامهی تورّیچلّی، سه ایراد مطرح کرد که نشان میدادند که در ک انتقال فشار در هوا تا چه اندازه برای همعصران مشکل بود: (1) اگر کاسه با سرپوشی بسته باشد، هوا بر روی سرپوش سنگینی میکند نه بر جیوه، و در نتیجه به داخل کاسه فرو خواهد ریخت؛ (2) وزن هوا در راستائی قائم از بالا به پایین عمل میکند، پس چگونه ممکن است از پایین به بالا به داخل لوله منتقل شود؟ (3) اجسام غوطه ور در یک سیال تحت اثر نیروی رانش ارشمیدس قرار دارند، پس جیوه باید با نیروئی هم ارز با یک ستون هوای مساوی به طرف بالا رانده شود. تورّیچلّی در نامهای به تاریخ 8 تیر 1023 پاسخی نوشت و ایرادها را دقیقاً به این شرح رد کرد: (1) اگر سرپوش «درجهی تراکم» هوای جای گرفته بین خود سرپوش و جیوه درون کاسه را تغییر ندهد، همه چیز به صورت پیشین باقی میماند-این نکته را میتوان با مثال یک استوانه چوبی نشان داد که وزنهای بر آن قرار داشته باشد و از میان با ورقهای آهنی قطع شود؛ در این حالت، تراکم در قسمت پایین مثل قبل باقی میماند؛ (2) سیّالها طبیعتاً به سمت پایین گرانیده میشوند، ولی «به هر سوی، حتی به سمت بالا، فشار میآورند و فوران میکنند»؛ (3) جیوهی درون لوله در هوا غوطه ور نیست. دو نامهی تورّیچلّی، از حیث مفاد، نظریه فشار هوا را، با اشارهای به آنچه بعداً به صورت اصل پاسکال درآمد، استادانه عرضه میکنند.
تورّیچلّی، بر طبق نوشتههای همعصرانش، پس از موفقیت در آزمایش، به مشاهده شرایط زندگی حیوانات کوچک (ماهیها، مگسها، پروانهها) در خلاً پرداخت. ولی نتایج بدست آمده تقریباً هیچ بودند، زیرا جانوران پیش از آن که به قسمت بالای لوله پس از واژگون کردن آن] برسند در اثر وزن جیوه لِه میشدند؛ و به نظر میرسد که کوششها برای تعیین این که آیا صوت در خلاً منتشر میشود نیز ناموفق بوده است. دوک بزرگ، فردیناندوی دوم، در گواهی قدردانی بزرگ خود، فرمانی صادر کرد که در آن از این آزمایش تورّیچلّی بسیار تمجید شده بود.
رونوشتهای دو نامه تورّیچلّی بین دانشمندان ایتالیایی دست به دست گشت و برای مرسن هم ارسال شد؛ مرسن، که در مهرماه 1023 به ایتالیا سفر میکرد، از فلورانس گذشت و خود تورّیچلّی آزمایش را برایش تکرار کرد. در هنگام برگشت به فرانسه، ضمن فراهم ساختن موجبات پیشرفت فعالیت نظری و تجربی، دوستانش را از آزمایش تورّیچلّی آگاه ساخت. وینچنتسو آنتینوری نوشت که کشف فشارسنج چهرهی فیزیک را عوض کرد درست به همان گونه که تلسکوپ ظاهر نجوم را، گردش خون چهرهی پزشکی را، و پیل وولتا ظاهر فیزیک مولکولی را دگرگون ساخت.
آثار منفرد بدین قرارند: Opera geomctrica. De sphaera et solidis .
sphaeralibus libri duo... De motu gravium natural iter descendentium فلورانس، 1644)، )et proiectorum libri duo. De dimensione parabola De sphaera et که بخش اول با عنوان طولانیش تجدید چاپ شد: De sphaeralibus libri duo in quibus Archimedis doctrina de sphaera et cylindro denuo componitur, latius promovetur et in omni specie solidorum, quae vel circa, vel intra sphaeram. ex conversione poligonorum regularium gigni possint universalius propagatur (بولونیا، 1692)» Lezioni accademiche، ویراسته توماسو بوناونتوری (فلورانس، 1715؛ چاپ دوم، میلان، 1813)؛ Sopra la bonifica/ione della» Raccolta d"autori che trattano del moto delle jS »«Valle di Chiana ‘acque
چهارم (فلورانس، 1768). دیگر نوشته های کوتاه در آثار تاریخی انتشار یافتند، که در زیر به آنها اشاره می شود.
اکثر نسخههای خطی آثار توریچلی، پس از تغییر و تحولهای پیچیده و وارد آمدن برخی صدمات بر آنها آن طور که در مقدمه Opere نقل شده است – در کتابخانه ملی مرکزی فلورانس محفوظند؛ آنجولو پروچیسی، در ) Evangelista Torricelli net terzo centenario della morte (فلورانس، 1951)، 109-77، فهرست دقیق مستندی از آنها به دست میدهد. آثار دستنویس، جز یکی، و یادگارهائی که در موزه توریچلی در فائنتسا نگهداری میشدند در 1944 از بین رفتند.
دو تصویر رنگ و روغنی از توریچلی در نگارخانه اوفیتسی در فلورانس موجود است. تصویری دیگر، گراوور شدهی پیئترو آنیکینی، در اولین صفحه Lezioni accademiche به چاپ رسیده است.
exceUentium qui saeculis XVII et XVIII floruerunt ، از آنجلو فابرونی، یکم (پیسا، 1778)، 340- 399، که ضمیمه آن شامل Racconto di alcuni problemiاست؛ و Notizie degli aggrandimenti delle scienze fisiche problemi accaduti in Toscana nel corso di anni LX del secolo XVII .(از جووانّی تارجونی توتستّی، 4 جلد (فلورانس، 1780).
نیز Notizie istoriche relative alTAccademia del cimento (از وینچنستو آنتینوری، در مجموعه مربوط به دانشمندان علوم طبیعی و آزمایشهائی که در فرهنگستان چیمنتو صورت پذیرفته اند (فلورانس، 1841)، در صفحات مختلف، بخصوص 27؛ Die Mechanik in ihrer Entwickelung historisch-kritisch dargeslellt ، از ارنست ماخ، چاپ دوم (لایپ تسیش، 1889)، 377 به بعد؛ و »
Storia del metodo sperimentale in Italia، از رافائلّو کاورنی، 6 جلد (فلورانس، 1891- 1900؛ تجدید چاپ، بولونیا، 1970)- جلدهای یکم، چهارم، پنجم، بخشهای چاپ نشدهای از آثار توریچلی را دارند.
پس از انتشار Opere، که بسیاری از نوشته های انتشار نایافته را شامل میشد، پژوهش دربارهی توریچلی نیروی محرک تازهای گرفت. آثار زیرین شامل مآخذ کتابشناختی متعدد دیگری میشوند: Sopra una Icnte di» Evangelista Torricelli، از واسکو رونکی، در L"universo (فلورانس)، 5، شماره 2 (1924)؛ Origini e sviluppi deliesperienza torricelliana ، از ماریوگلیوتسی (تورینو، 1931)، تجدید چاپ با اضافات در Opere ، چهارم، 231- 294؛L’experience barometrique ses antecedents et ses explications
»، از ک. دِ وارد (تووار، 1936)؛ و Le origini del calcolo infinitesimale nell"era modema ، از گوئیدو کاستلنوئووو (بولونیا، 1938؛ چاپ دوم، میلان، 1962)، در صفحات مختلف بخصوص 52- 53، 58- 62؛ L’opcra geomctrica di Evangelista Torricelli
، از اتّوره بورتولوتّی، در MMp، 48 (1939)، تجدید چاپ در Opere، چهارم، 301-337؛ »De infinitis spiralibus ( ATC ، از اتوره کاروتچو، مقدمه، تنظیم مجدد، ترجمه و یادداشتها به همت کاروتچو (پیسا، 1955)؛ Lettere a document! rignarolanti Evangelista Torricelli، از جوزپّه روسینی (فائنتسا، 1956)؛
Convegno di studi torricelliani in occasione del 350º anniversario della nascita di Evangelista Torricelli ، از همو (فائنتسا، 1959)؛ و The History of Barometer، از و. ا. نولز میدلتن (بالتیمور، 1964)، فصل 2.
منبع مقاله :
گیلیپسی، چارلز کولستون، (1387) زندگینامهی علمی دانشوران، ترجمه احمد آرام ... [و دیگران]، تهران: شرکت انتشارات علمی و فرهنگی، چاپ اول
Evangelista Torricelli
(ت. فائنتسا، ایتالیا، 23 مهر 987/ 15 اکتبر 1608؛ و، فلورانس، ایتالیا 3 آبان 1026/ 25 اکتبر 1647)، ریاضیات، فیزیک.
تورّیچلّی، که میان سه فرزند گاسپار تورّیچلّی و کاترینا آنجِتّی فرزند ارشد بود، به سرعت استعدادهای خارق العاده از خود نشان داد. پدرش، که بافندهای متوسّط الحال بود، پسر را نزد عمویش یاکوپو (آلسّاندروی سابق) راهب کامالدولی فرستاد تا بر تحصیل او در زبان، ادبیات، و آثار باستانی یونان و روم سرپرستی و نظارت کند. در 1004 و 1005 تورّیچلّی در جلسات درس ریاضیات و فلسفهی مدرسهی یسوعیان در فائنتسا حضور مییافت، و چنان استعداد برجستهای از خود بروز داد که عمویش متقاعد شد که او را برای تحصیل بیشتر به آموزشگاهی که به همت بندتّو کاستِلّی، عضو هم مسلک خودش، و ریاضیدان و مهندس ئیدرولیک و شاگرد پیشین گالیلئو، اداره میشد به رم بفرستد. کاستلّی دلبستگی فراوانی به این جوان پیدا کرد، نبوغ استثنایی او را تشخیص داد، و او را منشی خود ساخت.
مدرک مستقیم ما از دامنه و مسیر مطالعات علمی تورّیچلّی در مدت اقامتش در رم در نخستین نامه (21 شهریور 1011/ 11 سپتامبر 1632) از مکاتبات برجای ماندهی او است که از طرف کاستلّی، که خارج از رم بود، برای گالیلئو فرستاده شد. توْریچلّی، برای اعلام نامهای از گالیلئو به کاستلّی، فرصت را غنیمت شمرده خود را به عنوان ریاضیدانی حرفهای، متبحّری شایسته در هندسهی آپولونیوس، ارشمیدس و تئودوسیوس معرفی کرد؛ او افزود که آثار بطلمیوس را تحصیل کرده است و از طریق آثار برائه، کپلر، و لونگومونتانوس «تقریباً به همه چیز» پی برده است. این مطالعات او را ناگزیر کردهاند که اصول کوپرنیک را بپذیرد «و از لحاظ فرقه و حرفه پیرو گالیلئو» شود؛ او در رم نخستین کسی بود که در کتاب گالیلئو به نام Dialogo sopra i due massimi sistemi («گفتگو دربارهی دو نظام بزرگ»، که در فوریهی همان سال (1632/ بهمن ماه 1010) انتشار یافت مطالعهای دقیق کرده بود.
پس از این نامه تا سال 1031 وقفهای در مکاتبات وجود دارد، و معلوم نیست که تورّیچلّی در آن مدت کجا روزگار میگذرانده یا چه میکرده است. محتملترین فرضی که تاکنون اقامه شده این است که او از بهار 1009 تا بهمن 1019 در دستگاه عالیجناب جووانّی چامپولی، دوست و حامی گالیلئو، که از 1011 فرماندار شهرهای مختلف در مارکِس و اومبریا (مونتالتو، نورچا، سان سِوِرینو فابریانو) بود، منشیگری میکرد؛ تورّیچلّی بار دیگر در 1020در رم بود. او عقاید كاستلّى و ریاضیدانان دیگر را دربارهی رسالهای راجع به حرکت جویا شده بود که آموزهی حرکت پرتابهها را، که گالیلئو در سومین روز از Discorsi e dimostrazioni matematiche introno a due nuove scienze... («گفتارها و برهانهای ریاضی درباره دو علم جدید»، لیدن، 1638) بتفصیل بیان کرده بود، شرح و بسط میداد. کاستلّی این اثر را بسیار عالی میدانست؛ درباره آن با گالیلئو گفتگو نمود؛ و در فروردین پس از آن که تورّیچلّی را برگماشت تا در غیاب او تدریس کند، در راه سفرش از رم به ونیز از مسیر پیسا و فلورانس، دستنویسی را به گالیلئو تسلیم نمود، و پیشنهاد کرد که در تهیه و تنظیم دو «روز» که او فکر کرده است بعداً به «گفتارها...» اضافه کند تورّیچلّی را به عنوان دستیار بپذیرد. گالیلئو موافقت کرد و از تورّیچلّی دعوت نمود که در آرچتری به او ملحق شود.
ولی تاخیر کاستلّی در بازگشت به رم و مرگ مادر تورّیچلّی، که با فرزندان دیگرش به رم نقل مکان کرده بود، تورّیچلّی را ناگزیر کرد که ورود خود به آرچتری را تا 19 مهر 1020 به تعویق اندازد. او در خانهی گالیلئو، که قبلاً وینچنتسو ویویانی در آن زندگی میکرد، اقامت گزید، و تا زمان مرگ گالیلئو که در 19 دی 1020 فرارسید در دوستی نزدیک با او در آنجا ماند. در حالی که تورّیچلّی آماده بازگشتن به رم بود، فردیناندوی دوم، دوک بزرگ توسکانی، به پیشنهاد آندرئا آرّیگتّی، او را به مقام ریاضیدان و فیلسوف منصوب کرد، مقامی، با حقوق خوب و اقامت در کاخ مدیچی، که در اثر مرگ گالیلئو بیمتصدی مانده بود.
تورّیچلّی تا آخر عمر در فلورانس ماند. این سالها، یعنی خوشترین سالهای زندگی او، سرشار از بزرگترین فعالیت علمی بودند. دیری نکشید که وی، که در اثر طرز بیان آراسته و درخشان و لطیفه دارش احترام بسیار کسب کرد، با نمایندگان برجستهی فرهنگ فلورانسی-سالواتوره روزای نقاش، کارلوداتی آگاه از فرهنگ و ادب یونانی، و آندرئا آزیگتّیِ مهندس ئیدرولیک-طرح دوستی ریخت. در واقع، جلسات منظم با این دوستان سبب پیدایش «فرهنگستان پرکوسی» شد، که تورّیچلّی ظاهراً از کمدیهائی که مینوشت ایشان را باخبر میکرد؛ این کمدیها پس از مرگ او باقی نماندهاند ولی در خاطراتی که در بستر مرگش برای لودوویکو سرنایی دیکته کرد صریحاً ذکر شدهاند («مجموعه آثار»، چهارم، 88).
در سال 1023 تنها اثری که از تورّیچلّی در مدت زندگیش بچاپ رسید و دوک بزرگ تمام مخارج چاپ آن را متقبل شده بود، انتشار یافت. مجلّد Opera geometeica («آثار هندسی») به سه بخش تقسیم شده بود: بخش یکم مربوط میشد بهdu De Sphaera et solidis Sphaeralibus libri؛ بخش دوم مشتمل بود بر De motu gravium naturaliter descendentium et proiectorum (این نوشته به گالیلئو به پاس عقیدهاش تقدیم شد)؛ و بخش سوم عبارت بود از De dimemsione parabolae. این اثر، که در اندک زمانی در سراسر ایتالیا و اروپا شهرت یافت، ارزش ذاتی داشت، و بیان واضحش موجب شد که هندسهی کاوالیئری، که خواندن نوشتههایش دشوار بود، اشاعه یابد.
شهرتی که تورّیچلّی به عنوان هندسه دان کسب کرد سبب افزایش مکاتبات او با دانشمندان ایتالیایی و تعدادی از دانشمندان فرانسه [کارکاوی، مِرسِن، ف. دو وِردو، روبروال] شد که توسط ف. نیسرون، که هنگام اقامت در رم وی را ملاقات کرده بود، به آنان معرفی شد. این مکاتبات وسیلهی ابلاغ و انتقال بزرگترین کشفیات علمی تورّیچلّی و همچنین موجبی برای مباحثات شدید درباره حقّ تقدّم بودند، که در طول آن قرن جریان داشت. این مباحثات، مخصوصاً با روبروال دربارهی حقّ تقدّم کشف بعضی از خواص چرخزاد (cycloid)، از جمله تربیع، گرانیگاه، و اندازه گیری حجم حاصل از دَوَران آن حول قاعده، مشاجرات قلمی جدّیای بودند. توَرّیچلّی، برای دفاع از حقوق خود، تصمیم گرفت که تمام مکاتبات خود با ریاضیدانان فرانسوی را منتشر کند، و در 1025 شروع کرد به پیش نویسی اثری به نام Racconto d"alcuni problemi proposti e passati tra gli matematici di Francia et il Torricelli ne i quattro anni prossimamente passati («مجموعهی آثار»، سوم، 1-32). ولی هنگامی که به این کار مشغول بود به سبب ابتلا به بیماری شدیدی (احتمالاً تب حصبه)، که فقط چند روز به طول انجامید، وفات یافت. بنابر وصیّتش در کلیسای سان لورنتسو در فلورانس به خاک سپرده شد، ولی محلّ قبرش معلوم نیست.
توْرّیچلّی در تمام عمر به تحقیق در ریاضیات مشغول بود. در دوران جوانی آثار قدیمی و معتبر هندسهی یونانی را، که با روش حذف تصاعدی به مسائل مربوط به بینهایت کوچکها میپرداختند، فراگرفت. ولی از آغاز قرن هفدهم روش کلاسیک تا حدی جای خود را به فرایندهای شهودیتر داده بود؛ نخستین مثالها را کپلر بدست داد، که برای تعیین سطحها و حجمها از روشهای ارشمیدس دست برداشت و به شیوههای سریعتری روی آورد که از مسألهای تا مسأله دیگر فرق میکردند و به همین سبب بدشواری قابل تقلید بودند. کاوالیئری، پس از چندین سال تفکر، در هندسه بخش ناپذیرهای خود (1014)، به یک فرایند اساسی توجه کرد که روبرال، فرما، و دکارت هم تقریباً در همان سال در جهت آن حرکت کرده بودند؛ این تصادف نشان میدهد که زمان برای رویکردهای هندسی جدید فرارسیده بود.
هندسهی جدید هر شکل مسطح را متشکل از بینهایت تار در نظر میگرفت که به وسیلهی یک رشته خطوط مستقیم متوازی در داخل شکل جدا میشدند: سپس هر تار همچون مستطیل بینهایت باریکی انگاشته میشد که، بر طبق اصطلاحی که گالیلئو باب کرد، «بخش ناپذیر» نامیده میشد. از روابط مفروض یا محقق بین بخش ناپذیرها امکان استنتاج روابط بین مجموعها از طریق اصل کاوالیئری وجود داشت، که میتوان آن را چنین بیان نمود: دو شکل مسطح تقسیم شده بین خطوط مستقیم متوازی مفروض است؛ اگر همهی این خطوط مستقیم متوازی پارهخطهائی را در دو شکل مشخص سازند که رابطهی ثابتی داشته باشند، آنگاه مساحتهای دو شکل نیز همان رابطه را دارند. این اصل بآسانی به شکلهای فضایی بسط داده میشود. اصولاً هندسه کاوالیئری نخستین گام به سوی حساب بینهایت کوچکها بود، که به جای بینهایت بزرگ و بینهایت کوچکی ریاضی بالقوه هندسه دانان یونانی بینهایت بزرگ و بینهایت کوچکی حاضر را قرار داد.
تورّیچلّی، پس از تسلّط بر بیاعتمادی اولیه خود به روش نوین، از آن به عنوان ابزاری ابتکاری برای کشف قضایای جدیدی استفاده کرد که بعداً با روشهای قدیمی معتبر آنها را مدلل میکرد. کاربرد مختلط دو روش-یعنی روش بخش ناپذیرها برای کشف کردن و طریقهی ارشمیدس برای ثابت کردن-در کتاب «آثار هندسی» فراوان است. بخش یکم De Sphaera et solidis Sphaeralibus، که در حدود سال 1020 تألیف شده است، شکلهای حاصل از دوران یک چند ضلعی منتظم محاط در دایره یا محیط بر آن حول یکی از محورهای تقارن را (که قبلاً توسط ارشمیدس بیان شده بود) مورد بررسی قرار میدهد. تورّیچلّی مشاهده میکند که اگر چند ضلعی منتظم دارای اضلاع متساوی باشد، یکی از محورهای تقارنش دو رأس متقابل یا وسط دو ضلع متقابل را به هم وصل میکند؛ از طرف دیگر، اگر اضلاع آن مساوی نباشند، یکی از محورهای تقارنش یک رأس را به نقطه وسط ضلع مقابل وصل مینماید. او، براساس این مشاهده، احجام حاصل از چنین دَوَران را به شش قسم طبقه بندی میکند، خواص آنها را بررسی مینماید، و قضیههای جدید و روابط متریِ جدیدی برای اجسام گِرد (مدوّر) هندسهی مقدماتی عرضه میدارد. در بخش دوم کتاب، حرکت پرتابهها مورد بحث قرار میگیرد.
در بخش سوم، قطع نظر از درج بیست برهان برای قضیهی ارشمیدس دربارهی تربیع سهمی بدون اضافه کردن چیز تازهی مهمی به آن، تورّیچلّی نشان میدهد که سطح محصور بین چرخزاد و قاعدهاش مساوی سه برابر سطح دایرهی مولد آن است. به عنوان ضمیمهای بر این بخش از کار، پژوهشی دربارهی حجم حاصل از حرکت حلزونی شکل یک سطح مستوی بر گِرد محوری از صفحهاش وجود دارد، با اثبات این نکته که این حجم مساوی با حجم حاصل از دَوَران کامل آن سطح به گرد همان محور است. تورّیچلّی این قضیه ظریف را در مسائل متعدد بکار میبرد، بویژه برای رویه یک پیچ با رزوهای تخت که او مساوی بودن آن را با قسمت مناسبی از یک سهمیگون دارای یک گام نشان میدهد.
تورّیچلّی، همین که آشنایی فزایندهای با روشی بخش ناپذیرها پیدا کرد.-به گفتهی خود کاوالیئری-به نقطهی فوق استادی و مهارت رسید. در واقع او این نظریه را با استفاده از بخش ناپذیرهای منحنی، بر پایهی مفهوم اساسی زیر، بسط داد: برای مقایسه کردن دو شکل مسطح، اولی با مجموعی از منحنیها و دومی با مجموعی از خطوط مستقیم موازی تقسیم میشود: اگر هر بخش ناپذیر منحنی در اولی مساوی با بخشی ناپذیر متناظر در دومی باشد، مساحتهای دو شکل باهم برابرند. سادهترین مثال، مقایسهی یک دایرهی تقسیم شده به حلقههای هم مرکز بینهایت کوچک است با مثلثی تقسیم شده به تارهای بینهایت کوچک موازی با قاعده (قاعدهی این مثلث محیط دایره است که به صورت خط راست درآمده و ارتفاع مثلث شعاع آن دایره است). از تساوی حلقهها با نوارهای متناظر نتیجه میشود که مساحت دایره با مساحت مثلث برابر است.
این اصل به شکلهای فضایی نیز بسط داده شده است. تورّیچلّی درخشانترین کاربرد آن را در 1020 با اثبات قضیهای جدید، که گوهری در نوشتههای ریاضی زمان است، بدست داد. این قضیه، که در «آثار هندسی» منتشر شد، به شرح زیر است («مجموعهی آثار»، یکم، 191-213): نقطهای روی یک هذلولی متساوی الساقین (به معادلهی 1=xy) فرض کنید و سطحی را در نظر بگیرید که از مقطع نامحدود هذلولی دارای مجانب x، مجانب x، و عرض نقطهی انتخاب شده تشکیل شده باشد. اگرچه چنین سطحی از لحاظ اندازه نامتناهی است، جسمی که در اثر دَوَران این سطح حول مجانب به وجود میآید، هرچند از حیث وسعت نامحدود است، با وجود این دارای حجم محدودی است، که بر طبق محاسبه تورّیچلّی
 است، و a در آن طول نقطه مفروض در روی هذلولی است.
است، و a در آن طول نقطه مفروض در روی هذلولی است.برهان تورّیچلّی، که کاوالیئری آن را بسیار ستوده و فرما از آن تقلید کرده است، متضمن این فرض است که جسم حاصل از دوران مرکب است از تعداد بینهایت سطوح استوانهای شکل با محور، که همه آنها دارای مساحت جانبی مساوی هستند، همهی آنها در تناظر دو سویه با مقاطع یک استوانه مناسب قرار دارند، و همهی آنها مساوی با سطوح آن استوانهاند: اصل بخش ناپذیرهای منحنی این نتیجه را میدهد که حجم این استوانه مساوی با حجم جسمی است که از دَوَران مقطع هذلولی موردنظر ایجاد میشود. برطبق اصطلاحات جدید، روش کار تورّیچلّی با بیان این نکته توصیف میشود که هر انتگرالی در دستگاه مختصّات دکارتی جای خود را به انتگرالی در دستگاه مختصات استوانهای میدهد. تورّیچلّی، بازهم با استفاده از بخش ناپذیرهای منحنی، در میان کارهای دیگرش، حجم جسم محدود به دو سطح مستوی و هرگونه سطح جانبی، بویژه حجم بشکهها، را پیدا کرد. در 1022 نتایج برای فرما، و دکارت و روبروال فرستاده شد، و آنان آنها را بسیار دقیق و درست یافتند.
مورد هذلولی تورّیچلّی را وادار کرد که منحنیهای کلیتری را مطالعه کند که امروزه با معادلاتی که صورت
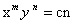 دارند تعریف میشوند؛ در این معادلات m و n اعداد درست مثبت و n≠ m است. وی کشف کرد که دَوَران این منحنیها حول یک مجانب ممکن است جسمی بینهایت دراز با حجم محدود ایجاد کند و، در شرایطی خاص، سطح محصور بین مجانب و منحنی نیز ممکن است محدود باشد. تورّیچلّی تصمیم گرفت که همهی این نتایج را موزون و هماهنگ کند؛ در سالهای 1025 و 1026 نتایج را در یک اثر فردی با عنوان De infinitis hyperbolis («هذلولیهای نامحدود») با نامه به ریاضیدانان متعدد ابلاغ کرد، ولی پیش از آن که بتواند آن را کامل کند وفات یافت. تنها پس از انتشار «مجموعه آثار» این امکان فراهم آمد که این مقاله از روی یاداشتهای پراکنده بازنویسی شود.
دارند تعریف میشوند؛ در این معادلات m و n اعداد درست مثبت و n≠ m است. وی کشف کرد که دَوَران این منحنیها حول یک مجانب ممکن است جسمی بینهایت دراز با حجم محدود ایجاد کند و، در شرایطی خاص، سطح محصور بین مجانب و منحنی نیز ممکن است محدود باشد. تورّیچلّی تصمیم گرفت که همهی این نتایج را موزون و هماهنگ کند؛ در سالهای 1025 و 1026 نتایج را در یک اثر فردی با عنوان De infinitis hyperbolis («هذلولیهای نامحدود») با نامه به ریاضیدانان متعدد ابلاغ کرد، ولی پیش از آن که بتواند آن را کامل کند وفات یافت. تنها پس از انتشار «مجموعه آثار» این امکان فراهم آمد که این مقاله از روی یاداشتهای پراکنده بازنویسی شود.هندسهی بخش ناپذیرها را تورّیچلّی در تعیین گرانیگاه شکلها نیز بکار برد. در نامهای به تاریخ 18 فروردین 1025 به میکلانجلو ریتچی، او «قضیهی کلی» را، که حتی امروز هم جامعترین قضیه ممکن انگاشته میشود، فاش ساخت، قضیهای که تعیین گرانیگاه هر شکل را از راه رابطه بین دو انتگرال میسر میسازد. از میان حالات خاص، باید اشاره به تعیین گرانیگاه قطاع مستدیری کرد که هم به طریقهی قدیمی و مرسوم و هم با روش بخش ناپذیرها بدست آمد. تورّیچلّی به همان نتیجهای رسید، و شاید هم میدانست، که شارل دو/ لافای در 1011 به آن رسیده بود.
تورّیچلّی توجه خود را به تعیین طول قوسهای یک منحنی نیز معطوف کرد، کاری که دکارت، پس از آن که از طریق مِرسِن اطلاع یافت که روبروال تساوی طول قوسهای خاصی از سهمی و طول قوسهای مارپیچ ارشمیدس را اثبات کرده است، در رساله یGéométrie («هندسه»، 1637) غیرممکن بودن آن را اعلام کرد. تورّیچلّی، با تصور «مارپیچ لوگاریتمی»، که آن را «هندسی» مینامید، روشی را آموخت که تعیین طول تمام قطعه واقع بین هر نقطه از منحنی و مرکز را، که منحنی پس از تعداد بینهایت دَوَران به آن میرسد، با خطکشی و پرگار میسر میکرد. علاوه بر این، او ثابت کرد که هر مارپیچ ارشمیدس-یا، بنا به گفتهی خود او، (مارپیچ حسابی»-را همواره میتوان با هر قوسی خاصی از یک منحنی سهمیگون مناسب مساوی ساخت.
تورّیچلّی، علاوه بر این خدماتی که به حساب انتگرال کرد، به تعدادی از روابط حساب دیفرانسیئل نیز پی برد. در میان بهرههائی که وی از مفهوم مشتق، مأخوذ از آموزه حرکت، گرفت (-پایین)، بجا است که ذکری از تحقیق وی دربارهی بیشینهها و کمینههاminima) ، (maxima به میان آید. او نشان داد که اگر مجموع x+y ثابت باشد، حاصل ضرب
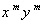 در صورتی بیشینه است که x و y در حالت نمایی همان را داشته باشند. وی همچنین نقطهای را که هنوز هم به نقطه تورّیچلّی معروف است روی سطح مثلثی معیّن کرد، که مجموع فواصل آن از رئوس مثلث کمینه است؛ این مسأله را فرما مطرح کرده بود.
در صورتی بیشینه است که x و y در حالت نمایی همان را داشته باشند. وی همچنین نقطهای را که هنوز هم به نقطه تورّیچلّی معروف است روی سطح مثلثی معیّن کرد، که مجموع فواصل آن از رئوس مثلث کمینه است؛ این مسأله را فرما مطرح کرده بود.تورّیچلّی، ضمن مطالعاتش در زمینه مکانیک، خدمات مهم دیگری هم به ریاضیات کرد. در رسالهی De motu gravium، وی بررسی حرکت سهمیگون پرتابهها را، که گالیلئو آغازگر آن بود، ادامه داد، و مشاهده کرد که اگر نیروی شتابگر در هر نقطه از مسیر حذف شود، پرتابه در راستای مماسی بر مسیر حرکت خواهد کرد. او این مشاهدات را، که موجب تحسین گالیلئو بودند، برای رسم مماس بر نقطهای از مارپیچ ارشمیدس، یا چرخزاد، مورد استفاده قرار داد، با در نظر گرفتن این که منحنیها به وسیله نقطهای که دارای دو حرکت همزمان است رسم شوند. این موضوع در یادداشتهای انتشار نیافته به گونهای کاملاً جامعتر بررسی شده است. نقطهای در نظر گرفته شده است که دارای دو حرکت همزمان، یکی یکنواخت و دیگری متغیر، در امتداد دو خط راست عمود برهم است. تورّیچلّی، پس از ترسیم منحنی مسافت به عنوان تابع زمان، نشان میدهد که خط مماس بر هر نقطه از منحنی با محور زمان زاویهای میسازد که تانژانت آن اندازه سرعت جسم متحرک در آن نقطه را بدست میدهد. اصولاً این موضوع تأییدی است بر این که عملیات انتگرال گیری و مشتق گیری سرشتی عکس یکدیگر دارند. این نکته قضیه اساسی حساب جامع و فاضلی را تشکیل میدهند که آیزک بَرو آن را در 1049 انتشار داد، و از میان پیشینیانش از گالیلئو، کاوالیئری، و تورّیچلّی نام برد. ولی حتی برو هم اهمیت قضیه را، که نخستین بار به همّت نیوتن به اثبات رسید، درک نکرد.
برتری کامل روشهای هندسی جدید تورّیچلّی را از خطرهای ذاتی آگاه ساخت، به طوری که دستنویسهای او حاوی مطالبی بر ضد بینهایتها است. نوشتههای انتشار نیافتهی وی، در واقع، مجموعهای از باطلنما (پارادوکس)هائی را در بر دارند که آموزه بخش ناپذیرها، اگر با احتیاطهای لازم بکار برده نشوند، به آنها میانجامند.
تورّیچلّی در De motu grauium درصدد است که اصل گالیلئو دربارهی تساوی سرعتهای سقوط آزاد وزنهها در امتداد سطحهای شیبدار با ارتفاع مساوی را به اثبات رساند. او اثبات خود را بر پایه اصل دیگری بنا میکند که اکنون اصل تورّیچلّی نامیده میشود ولی بر گالیلئو معلوم بود؛ بر طبق این اصل، دستگاهی صُلب مرکب از تعدادی جسم فقط در صورتی میتواند به خودی خود بر سطح زمین حرکت کند که گرانیگاه آن پایین برود. تورّیچلّی، پس از بکار بستن این اصل در حرکت بر روی وترهای دایره و سهمی، به حرکت پرتابهها روی میآورد و، با تعمیم دادن آموزه گالیلئو، پرتاب تحت هر زاویه مایل را در نظر میگیرد- در صورتی که گالیلئو فقط پرتاب افقی را منظور داشته بود. او مشاهده اتفاقی گالیلئو را به صورتی کلی اثبات میکند که اگر پرتابهای در هر نقطه از مسیر با سرعتی مساوی با سرعت مکتسب در آن نقطه در جهت مخالف از نو پرتاب شود، همان مسیر را در جهت معکوس خواهد پیمود. این گزاره هم ارز است با این گفته که پدیدههای دینامیکی برگشت پذیرند- یعنی زمانِ مطرح شده در مکانیک گالیلئو ترتیب دارد اما فاقد جهت است. تورّیچلّی، در زمرهی تعدادی از قضایای علم پرتابههای خارجی، نشان داد که سهمیهای متناظر با سرعت اولیهی معین و متناظر با میلهای متفاوت، همه بر سهمی واحدی مماسند (معروف به سهمی ایمنی یا سهمی تورّیچلّی، که نخستین مثال از منحنی پوش دستهای از منحنیها است).
رساله با پنج جدول عددی به پایان میرسد. چهار جدول اول آن جدول مثلثاتی هستند که بترتیب مقادیر
 ، را برای هر یک از درجههای بین
، را برای هر یک از درجههای بین  و
و  بدست میدهند؛ با این جدولها، وقتی که سرعت اولیه و زاویهی پرتاب معیّن باشند، بقیهی اجزای مشخصهی مسیر را میتوان حساب کرد. جدول پنجم زاویهی پرتاب را، وقتی که فاصلهی فرود گلوله و بیشینه برد اسلحه معلوم باشند، بدست میدهد. در تحلیل نهایی، اینها جداول پرتاب گلوله توپ هستند، که ارزش عملی آنها به سبب شرح کاربردشان به زبان ایتالیایی، که درکش برای توپچیان آسانتر از لاتینی است، بیشتر میشود. زبان ایتالیایی همچنین در شرح پایانی جدول جدیدی بکار رفته است و این امر محاسبه ارتفاع اسلحه را برای افسران توپخانه آسان میسازد.
بدست میدهند؛ با این جدولها، وقتی که سرعت اولیه و زاویهی پرتاب معیّن باشند، بقیهی اجزای مشخصهی مسیر را میتوان حساب کرد. جدول پنجم زاویهی پرتاب را، وقتی که فاصلهی فرود گلوله و بیشینه برد اسلحه معلوم باشند، بدست میدهد. در تحلیل نهایی، اینها جداول پرتاب گلوله توپ هستند، که ارزش عملی آنها به سبب شرح کاربردشان به زبان ایتالیایی، که درکش برای توپچیان آسانتر از لاتینی است، بیشتر میشود. زبان ایتالیایی همچنین در شرح پایانی جدول جدیدی بکار رفته است و این امر محاسبه ارتفاع اسلحه را برای افسران توپخانه آسان میسازد.در یک بند از رساله به حرکت آب نیز با چنان اهمیتی اشاره شده است که ارنست ماخ تورّیچلّی را بنیاد گذار ئیدرودینامیک اعلام کرد. هدف تورّیچلّی این بود که سرعت ریزش مایعی را که از سوراخ کوچک ته ظرفی بیرون میریزد معین کند. او به کمک آزمایش متوجه شده بود که هرگاه مایع رو به بالا فوران میکرد، فواره به ارتفاعی میرسید که پایینتر از سطح مایع در ظرف بود. بنابراین، فرض کرد که اگر همهی مقاومتها در مقابل حرکت به صفر برسند، فواره به سطح مایع خواهد رسید. از این فرضیه، که هم ارز اصل بقا است، قضیهای را استنتاج کرد که نام او را بر خود دارد: سرعت فوران مایع در نقطه خروج برابر با سرعتی است که یک قطره میداشت اگر میتوانست از سطح آزاد مایع بالای سوراخ در خلاً به طور آزاد سقوط کند. تورّیچلّی همچنین نشان داد که اگر سوراخ در جدار ظرف ایجاد شود، مسیر فوران مایع به شکل سهمی خواهد بود؛ سپس آن بند از رساله را با مشاهدات جالب توجه دربارهی از هم پاشیدن جریان مایع به صورت قطرهها و دربارهی اثرهای مقاومت هوا به پایان رسانید. مهارت تورّیچلّی در علم ئیدرولیک برای همعصرانش چنان بخوبی شناخته شد که دربارهی پاکسازی درهی رود کیانا از آبهای راکد با او مشورت کردند، و او روش خاکریزی را برای احیای آن پیشنهاد کرد.
تبدیل «دما بین» (ترموسکوپ) گازیِ ابتداییِ گالیلئو به دماسنج (ترمومترِ) مایعی، که نخست با آب و بعد با الکل پرشد، اغلب به توْرّیچلّی نسبت داده شده، اگرچه گاهی هم فکر آن از دوک بزرگ فردیناندوی دوم دانسته شده است. از طرف دیگر، مدرک بسیار خوبی از توانایی فنی او در ساخت عدسیهای تلسکوپ وجود دارد، مهارتی که به احتمال قریب به یقین در مدت اقامتش در فلورانس آن را کسب کرده بود. او تا پاییز 1021 توانایی ساختن عدسیهای نسبتاً خوبی را بدست آورده بود، هرچند به پای عدسیهای عالیای که فرانچسکو فوانتانا، نامدارترین تلسکوپساز ایتالیایی آن زمان، میساخت نمیرسیدند. تورّیچلّی دست به کار شده بود تا با فونتانا رقابت کند و از او پیش افتد. تا 1022 توانست عدسیهائی مانند عدسیهای فونتانا، حتی شاید بهتر، تهیه کند، ولی بالاتر از همه متوجه شد که آنچه در واقع برای کارایی یک عدسی اهمیت دارد تراش کاملاً کروی سطح آن است، که وی با فنون ظریف انجام میداد. کارایی عدسیهای تورّیچلّی را دوک بزرگ تأیید کرد، و در 1023 به توْریچلّی گردن بندی طلا حامل ایک مدال با عبارت «Virtutis praemia» اهدا کرد.
شهرت عدسیهای عالی تورّیچلّی بسرعت همه جا منتشر شد و او سفارشهای زیاد دریافت میکرد و ثروت خوبی بدست آورد. وی کارایی تلسکوپهای مجهز به عدسیهایش را به طریقهی تراشی نسبت میداد که در آن زمان به صورت راز نگهداشته شد، ولی در برخی از مقالات توصیف گردید که پس از مرگ تورّیچلّی به دوک بزرگ انتقال یافتند، و او آنها را به ویویانی سپرد، که بعد از آن گم شدند. گاهی داستان ماهرانهای درباره این «راز» ساخته شده است؛ ولی بازسازی کامل «راز» تورّیچلّی از مدرکهای برجا مانده ممکن به نظر میرسد- که، قطع نظر از نیاز به بالابردن شایستگیهای محصول کارش در نظر دوک بزرگ، عمدتاً عبارت بودند از تراش و پرداخت بسیار دقیق سطوح، انتخاب شیشهی مرغوب، و محکم نکردن عدسیها «با زِفت یا به هر طریق با آتش». ولی این احتیاط آخری که، بنا به گفته تورّیچلّی، فقط خدا و خودش از آن خبر داشتند- از طرف هیئرونیموس سیرتوری در Telescopium او از 997 توصیه شده بود. در هر حال، یکی از عدسیهای تلسکوپی تورّیچلّی، که اکنون همراه با یادگارهای دیگر در «موزهی سرگذشت علم» در فلورانس نگهداری میشود، در 1303 توسط واسکو روانکی با استفاده از توری پراش معاینه شد. معلوم شد که کیفیت ساخت آن چندان استادانه و عالی است که یک وجه آن ظاهراً بهتر از آیینهای که عنوان سطح مرجع را داشت تراشیده و پرداخت شده، و با پیشرفتهترین شیوهی آن دوره ساخته شده است.
سخنرانیهائی که تورّیچلّی به مناسبتهای مختلف ایراد کرد، و توماسو بوناونتوری آنها را در کتابی با عنوان Lezioni accademiche («دروس فرهنگستانی») گرد آورد که پس از درگذشت وی انتشار یافت، مرجّحاً درباره موضوعات فیزیکی بودند. آنها عبارتند از هشت سخنرانی در فرهنگستان کروسکا، که وی یکی از اعضای آن بود (یک سخنرانی برای سپاسگزاری به مناسبت پذیرفته شدن در فرهنگستان، سه تا درباره نیروی برخورد، دو تا دربارهی سُبکی، یکی راجع به باد، و یکی دربارهی شهرت)؛ یک سخنرانی در ستایش ریاضیات، که در کارگاه هنری فلورانس ایراد شد؛ دو سخنرانی دربارهی معماری نظامی در فرهنگستان نقشه کشی؛ و یکی در ستایش از «قرن طلایی»، عصر افسانهای کمال انسانی، که در «فرهنگستان پرکوسّی» ایراد شد.
سخنرانیهای مربوط به نیروی برخورد و دربارهی باد، از دیدگاه علم فیزیک، از جاذبه و اهمیت خاصی برخوردارند. وی در اولی گفت که گزارش دهندهی عقایدی است که گالیلئو در گفتگوهای غیررسمی آنان ابراز کرده است، و در آن مشاهدات و آرای اصیل و ابتکاری وجود دارد. به عنوان مثال، مکسول این ادعا را که «نیروها و قوهی حرکت» (چیزی که آن را کارمایه [انرژی] مینامیم) در اجسام نهفتهاند در آخرین بند ازTreatise on Electricity and magnetism («رساله دربارهی برق و مغناطیس»، 1873) بدین معنی تعبیر کرده است که انتشار کارمایه یک عمل با واسطه است نه عملی از دور، تورّیچلّی، در سخنرانی راجع به باد، نظریهی رایج تشکیل باد را رد کرد؛ بر طبق آن عقیده، باد ناشی از بازدمهای بخارداری بود که از زمین مرطوب ایجاد میشد؛ از طرف دیگر، این نظریه جدید را مطرح کرد که بادها در اثر اختلاف دمای هوا، و در نتیجه اختلاف چگالی، بین دو ناحیهی زمین ایجاد میشوند.
ولی، بالاتر از همه، نام تورّیچلّی با آزمایشی برای سنجیدن فشار هوا پیوسته است که به نام او خوانده میشود. بحث درباره خلا یا پری (ملأ) تا نخستین مکاتب فلسفی یونان به عقب برمیگردد. در قرون وسطی، الهیات کاتولیکی آموزه ارسطو را که خلاً تناقضی است در منطق کنار زد و این مفهوم را به جای آن نشاند که طبیعت از خلاً نفرت دارد (امتناع از خلأ، horror vacui). در دورهی رنسانس بحث بین طرفداران خلأ و طرفداران ملأ دوباره بالا گرفت، گالیلئو، با پیوستن به تلزیو و برونو، فلاسفهی خردگرا، با استدلالهای ارسطو درباره خلأ به مخالفت برخاست و در حدود سال 992 وزن داشتن هوا را با آزمایش اثبات کرد. ولی، همانند اکثریت همعصران خود، معتقد بود که هیچ عنصری به خودی خود دارای وزن نیست؛ از این رو بر پایهی وزن معیّن شدهی هوا، نمیتوانست فشارهای درون هوای جوّ را استنتاج کند. برای توضیح این پدیده که آب در تلمبههای مکنده بیش از هجده «براتچا» (braccia، تقریباً نه متر) بالا نمیآید، چنان که چاه کنان فلورانسی مشاهده کرده بودند، گالیلئو فرضیهی یک نیرو-«نیروی خلأ»- را مطرح کرد که درون تلمبه یافت میشد و میتوانست تعادل ستونی از آب به ارتفاع هجده براتچا را حفظ کند.
در 1009، هنگامی که جووانّی باتّیستا بالیانی از وی پرسید که چرا سیفونی که از روی تپهای به ارتفاع حدود بیست و یک متر گذشته است کار نمیکند، گالیلئو در پاسخ چند بار نظریهاش دربارهی نیروی خلأ را تکرار کرد. بالیانی با ردّ پاسخ گفت که به عقیده وی کار نکردن سیفون ناشی از وزن هوا است که، با فشار آوردن به همهی اطراف، ستون آبی را نگه میدارد که در قسمت بالای سیفون تحت فشار نیست، و هوای سیفون هم در اثر جریان آبی که آن را پر میکند خارج شده است. ولی گالیلئو عقاید بالیانی را نپذیرفت، و در «گفتارها» (1638) همچنان به حمایت از نظریه «نیروی خلأ» ادامه داد. پس از مرگ گالیلئو بحث بین پیروانش در رم و فلورانسی ادامه یافت؛ و محتمل است که پیروانش در رم به تورّیچلّی روی آورده باشند تا عقیده او را درباره طرز کار تلمبههای مکنده یا درباره آزمایش مشابهی جویا شوند که گفته میشود گاسپارو برتی در 1019 در رم انجام داده است تا نشان دهد که آب در تلمبههای مکنده بیش از هجده براتچا بالا میرود.
تورّیچلّی، که شاید با تصور بالیانی آشنا بود، به تکرار آزمایش برتی یا بالیانی پرداخت؛ و در آن از مایعهای رفته رفته سنگینتر مانند آب دریا، عسل، و جیوه، که در توسکانی استخراج میشد، استفاده کرد. استفاده از جیوه همچنین به او امکان داد که، با قرار دادن یک لولهی شیشهای سادهی تقریباً یک متری به جای سیفون بالیانی یا برتی، عمل پرکردن را آسان کند. او طرح ریزی کرد که لوله را تا لبه آن از جیوه پرکند، دهانهی آن را با انگشت ببندد و آن را وارونه سازد، و دهانه باز آن را در جیوه درون کاسهای فرو برد. ساختن چنین لولهی درازی که بتواند وزن جیوه را تحمل کند در آن زمان کار آسانی نبود (فقط در 1025 مرسِن توانست لوله به قدر کافی محکمی از کارخانه شیشه سازی فرانسه تهیه کند)؛ تورّیچلّی از ویویانی خواست که یکی برایش بسازد، و به این ترتیب ویویانی نخستین کسی بود که آزمایش را انجام داد.
توْرّیچلّی، در نامهای به تاریخ 22 خرداد 1023 به میکلانجلو ریتچی، آزمایش را شرح داد و، با رد کردن نظریهی نیروی خلأ آن را مطابق گفته بالیانی تفسیر کرد. اما وی حتی پیش از انجام دادن آزمایش از تغییرات فشار جو اطلاع داشت، زیرا در نامهاش متذکر میشود که «می خواست اسبابی بسازد که تغییرات هوا را نشان دهد: یک زمان سنگینتر و چگالتر، یک زمان سبکتر و رقیقتر. برطبق فرضیهای نسبتاً مستند و اساسی، او ضمن مشاهده استادانهی رفتار اسباب بازیهای ئیدروستاتیکی، که شاید توسط خود او اختراع شده و بعداً «شیطانکهای دکارتی» نامیده شدند، اطلاعاتی دربارهی فشار جو بدست آورده بود. به گفته تورّیچلّی، نیروئی که ستون جیوه را نگه میدارد نیروی درون لوله تا بلکه نیروی خارجی حاصل از جو است که وزن آن بر جیوه درون کاسه نیرو وارد میکند. اگر به جای جیوه، لوله حاوی آب باشد، ارتفاع ستون آب، بر طبق پیش بینی تورّیچلّی، به نسبت فزونی سنگینی جیوه بیشتر خواهد بود، و این نتیجهای بود که در 1026 توسط پاسکال به اثبات رسید. در تأیید این فرضیه که علّت نگه داشته شدن جیوه [در لوله] امری است خارجی نه داخلی، تورّیچلّی به شرح آزمایشهای دیگری با لولهها میپردازد که، با دمیدن در یک کره از بالای آن، ستونهای جیوه به ارتفاعهای مساوی در لولهها بدست میآمدند، به طوری که نیرو از حجم خلاً ناشی نمیشد و بنابراین «نیروی خلأ» در میان نبود.
ریتچی، در پاسخ خود به نامهی تورّیچلّی، سه ایراد مطرح کرد که نشان میدادند که در ک انتقال فشار در هوا تا چه اندازه برای همعصران مشکل بود: (1) اگر کاسه با سرپوشی بسته باشد، هوا بر روی سرپوش سنگینی میکند نه بر جیوه، و در نتیجه به داخل کاسه فرو خواهد ریخت؛ (2) وزن هوا در راستائی قائم از بالا به پایین عمل میکند، پس چگونه ممکن است از پایین به بالا به داخل لوله منتقل شود؟ (3) اجسام غوطه ور در یک سیال تحت اثر نیروی رانش ارشمیدس قرار دارند، پس جیوه باید با نیروئی هم ارز با یک ستون هوای مساوی به طرف بالا رانده شود. تورّیچلّی در نامهای به تاریخ 8 تیر 1023 پاسخی نوشت و ایرادها را دقیقاً به این شرح رد کرد: (1) اگر سرپوش «درجهی تراکم» هوای جای گرفته بین خود سرپوش و جیوه درون کاسه را تغییر ندهد، همه چیز به صورت پیشین باقی میماند-این نکته را میتوان با مثال یک استوانه چوبی نشان داد که وزنهای بر آن قرار داشته باشد و از میان با ورقهای آهنی قطع شود؛ در این حالت، تراکم در قسمت پایین مثل قبل باقی میماند؛ (2) سیّالها طبیعتاً به سمت پایین گرانیده میشوند، ولی «به هر سوی، حتی به سمت بالا، فشار میآورند و فوران میکنند»؛ (3) جیوهی درون لوله در هوا غوطه ور نیست. دو نامهی تورّیچلّی، از حیث مفاد، نظریه فشار هوا را، با اشارهای به آنچه بعداً به صورت اصل پاسکال درآمد، استادانه عرضه میکنند.
تورّیچلّی، بر طبق نوشتههای همعصرانش، پس از موفقیت در آزمایش، به مشاهده شرایط زندگی حیوانات کوچک (ماهیها، مگسها، پروانهها) در خلاً پرداخت. ولی نتایج بدست آمده تقریباً هیچ بودند، زیرا جانوران پیش از آن که به قسمت بالای لوله پس از واژگون کردن آن] برسند در اثر وزن جیوه لِه میشدند؛ و به نظر میرسد که کوششها برای تعیین این که آیا صوت در خلاً منتشر میشود نیز ناموفق بوده است. دوک بزرگ، فردیناندوی دوم، در گواهی قدردانی بزرگ خود، فرمانی صادر کرد که در آن از این آزمایش تورّیچلّی بسیار تمجید شده بود.
رونوشتهای دو نامه تورّیچلّی بین دانشمندان ایتالیایی دست به دست گشت و برای مرسن هم ارسال شد؛ مرسن، که در مهرماه 1023 به ایتالیا سفر میکرد، از فلورانس گذشت و خود تورّیچلّی آزمایش را برایش تکرار کرد. در هنگام برگشت به فرانسه، ضمن فراهم ساختن موجبات پیشرفت فعالیت نظری و تجربی، دوستانش را از آزمایش تورّیچلّی آگاه ساخت. وینچنتسو آنتینوری نوشت که کشف فشارسنج چهرهی فیزیک را عوض کرد درست به همان گونه که تلسکوپ ظاهر نجوم را، گردش خون چهرهی پزشکی را، و پیل وولتا ظاهر فیزیک مولکولی را دگرگون ساخت.
کتابشناسی
یکم کارهای اصلی.
نوشته ها و مکاتبات علمی در کتابی انتشار یافتند با عنوان Opera di Evangelista Torricelli، ویراسته جینالوریا و جوزپه واسورا، 4 جلد، در پنج بخش (یکم تا سوم، فائنستا، 1919؛ چهارم، 1944)آثار منفرد بدین قرارند: Opera geomctrica. De sphaera et solidis .
sphaeralibus libri duo... De motu gravium natural iter descendentium فلورانس، 1644)، )et proiectorum libri duo. De dimensione parabola De sphaera et که بخش اول با عنوان طولانیش تجدید چاپ شد: De sphaeralibus libri duo in quibus Archimedis doctrina de sphaera et cylindro denuo componitur, latius promovetur et in omni specie solidorum, quae vel circa, vel intra sphaeram. ex conversione poligonorum regularium gigni possint universalius propagatur (بولونیا، 1692)» Lezioni accademiche، ویراسته توماسو بوناونتوری (فلورانس، 1715؛ چاپ دوم، میلان، 1813)؛ Sopra la bonifica/ione della» Raccolta d"autori che trattano del moto delle jS »«Valle di Chiana ‘acque
چهارم (فلورانس، 1768). دیگر نوشته های کوتاه در آثار تاریخی انتشار یافتند، که در زیر به آنها اشاره می شود.
اکثر نسخههای خطی آثار توریچلی، پس از تغییر و تحولهای پیچیده و وارد آمدن برخی صدمات بر آنها آن طور که در مقدمه Opere نقل شده است – در کتابخانه ملی مرکزی فلورانس محفوظند؛ آنجولو پروچیسی، در ) Evangelista Torricelli net terzo centenario della morte (فلورانس، 1951)، 109-77، فهرست دقیق مستندی از آنها به دست میدهد. آثار دستنویس، جز یکی، و یادگارهائی که در موزه توریچلی در فائنتسا نگهداری میشدند در 1944 از بین رفتند.
دو تصویر رنگ و روغنی از توریچلی در نگارخانه اوفیتسی در فلورانس موجود است. تصویری دیگر، گراوور شدهی پیئترو آنیکینی، در اولین صفحه Lezioni accademiche به چاپ رسیده است.
دوم. خواندنیهای فرعی.
در همهی کتابهای تاریخ ریاضیات یا فیزیک کم و بیش به نحوی کامل به بررسی زندگی و آثار توریچلی پرداخته شده است. Opere، جلد چهارم، 341- 346، حاوی یک کتابشناسی است. برخی از مهمترین آثار بدین قرارند: Lettera ai Filaleti. Della vera storia della cicloide e della famosissima esperienza dell"argento vivo، از تیمائورو آنتیانه (نام مستعار کارلو داتی) (فلورانس، 1663)، که نخستین اثری است که مکاتبات توریچلی با ریتچی درباره آزمایش مربوط به هواسنجی در آن به چاپ رسیده است؛ نوشتهای از توماسو بوناونتوری، در Lezioni accademiche ، پیشگفتار، پنج- چهل و نه؛ Vitae Italorum doctrinaexceUentium qui saeculis XVII et XVIII floruerunt ، از آنجلو فابرونی، یکم (پیسا، 1778)، 340- 399، که ضمیمه آن شامل Racconto di alcuni problemiاست؛ و Notizie degli aggrandimenti delle scienze fisiche problemi accaduti in Toscana nel corso di anni LX del secolo XVII .(از جووانّی تارجونی توتستّی، 4 جلد (فلورانس، 1780).
نیز Notizie istoriche relative alTAccademia del cimento (از وینچنستو آنتینوری، در مجموعه مربوط به دانشمندان علوم طبیعی و آزمایشهائی که در فرهنگستان چیمنتو صورت پذیرفته اند (فلورانس، 1841)، در صفحات مختلف، بخصوص 27؛ Die Mechanik in ihrer Entwickelung historisch-kritisch dargeslellt ، از ارنست ماخ، چاپ دوم (لایپ تسیش، 1889)، 377 به بعد؛ و »
Storia del metodo sperimentale in Italia، از رافائلّو کاورنی، 6 جلد (فلورانس، 1891- 1900؛ تجدید چاپ، بولونیا، 1970)- جلدهای یکم، چهارم، پنجم، بخشهای چاپ نشدهای از آثار توریچلی را دارند.
پس از انتشار Opere، که بسیاری از نوشته های انتشار نایافته را شامل میشد، پژوهش دربارهی توریچلی نیروی محرک تازهای گرفت. آثار زیرین شامل مآخذ کتابشناختی متعدد دیگری میشوند: Sopra una Icnte di» Evangelista Torricelli، از واسکو رونکی، در L"universo (فلورانس)، 5، شماره 2 (1924)؛ Origini e sviluppi deliesperienza torricelliana ، از ماریوگلیوتسی (تورینو، 1931)، تجدید چاپ با اضافات در Opere ، چهارم، 231- 294؛L’experience barometrique ses antecedents et ses explications
»، از ک. دِ وارد (تووار، 1936)؛ و Le origini del calcolo infinitesimale nell"era modema ، از گوئیدو کاستلنوئووو (بولونیا، 1938؛ چاپ دوم، میلان، 1962)، در صفحات مختلف بخصوص 52- 53، 58- 62؛ L’opcra geomctrica di Evangelista Torricelli
، از اتّوره بورتولوتّی، در MMp، 48 (1939)، تجدید چاپ در Opere، چهارم، 301-337؛ »De infinitis spiralibus ( ATC ، از اتوره کاروتچو، مقدمه، تنظیم مجدد، ترجمه و یادداشتها به همت کاروتچو (پیسا، 1955)؛ Lettere a document! rignarolanti Evangelista Torricelli، از جوزپّه روسینی (فائنتسا، 1956)؛
Convegno di studi torricelliani in occasione del 350º anniversario della nascita di Evangelista Torricelli ، از همو (فائنتسا، 1959)؛ و The History of Barometer، از و. ا. نولز میدلتن (بالتیمور، 1964)، فصل 2.
منبع مقاله :
گیلیپسی، چارلز کولستون، (1387) زندگینامهی علمی دانشوران، ترجمه احمد آرام ... [و دیگران]، تهران: شرکت انتشارات علمی و فرهنگی، چاپ اول



.jpg)












