تألیف: حمید وثیق زاده انصاری
منبع: راسخون
منبع: راسخون
آزمون دو طرفه یک اتفاق خارق العاده (شبیه به روی داد عجیب و غریب طبیعت مانند مار دو سر!) نیست و هم چنین مقابله با آن هم سخت نیست! در این مقاله اطلاعاتی در مورد این ابزار آماری ارائه خواهد شد.

در واقع ﻫﺮ ﺣﻜﻤﻲ درﺑﺎره ﺗﻮزﻳﻊ ﺟﺎﻣﻌﻪ ﻳﺎ ﭘﺎراﻣﺘﺮ ﺟﺎﻣﻌﻪ را ﻳﻚ ﻓﺮض آﻣﺎری می نامند و ﻣﻤﻜﻦ است درست یا نا درست باشد. درست یا نا درست بودن یک فرض، باید بر مبنای اطلاعات حاصل از نمونه گیری از جامعه بررسی شود. این عمل را آزمون فرض می نامیم. چون ادعا ممکن است درست یا نا درست باشد، بنا بر این دو فرض مکمل به وجود می آید: یکی برای آن که ادعا درست باشد و دیگری برای این که ادعا درست نباشد، بنا بر این شروع یک آزمون فرض، همواره شامل دو فرض آماری می باشد که در مقابل یک دیگر قرار می گیرند.
در ﺑﺤﺚ آزﻣﻮن ﻓﺮض اﻏﻠﺐ ﺑﺎ ﻓﺮض ﻫﺎ ﻳﺎ ادﻋﺎﻫﺎیی در ﻣﻮرد ﭘﺎراﻣﺘﺮﻫﺎی ﺗﻮزﻳﻊ ﺟﻮاﻣﻊ آماری مواجه هستیم. به این فرض یا ادعاها فرض صفر گفته می شود و آن را با نشان می دهند. فرض آماری که در مقابل فرض صفر قرار می گیرد (ناقض فرض صفر) را فرض مقابل نامیده و آن را با
نشان می دهند. فرض آماری که در مقابل فرض صفر قرار می گیرد (ناقض فرض صفر) را فرض مقابل نامیده و آن را با  نشان می دهند. ناحیه رد یک آزمون بر مبنای ساختار فرض مقابل
نشان می دهند. ناحیه رد یک آزمون بر مبنای ساختار فرض مقابل  تعیین می-گردد. توزیع آماره آزمون، به دو ناحیه تقسیم می شود، یکی ناحیه رد
تعیین می-گردد. توزیع آماره آزمون، به دو ناحیه تقسیم می شود، یکی ناحیه رد  و دیگری ناحیه قبول (عدم رد) H0، ناحیه رد فرض
و دیگری ناحیه قبول (عدم رد) H0، ناحیه رد فرض  را ناحیه بحرانی و مرز بین دو ناحیه رد و قبول را مقادیر بحرانی می نامیم. در واقع مقادیر بحرانی، ناحیه رد را از قبول جدا می کند.
را ناحیه بحرانی و مرز بین دو ناحیه رد و قبول را مقادیر بحرانی می نامیم. در واقع مقادیر بحرانی، ناحیه رد را از قبول جدا می کند.
يك آزمون دو طرفه آزمونی است كه در آن فرض با عبارت "مخالف است با" همراه است. ﺑﻪ ﻋﺒﺎرت دﻳﮕﺮ آزمون به صورت زیر باشد:
با عبارت "مخالف است با" همراه است. ﺑﻪ ﻋﺒﺎرت دﻳﮕﺮ آزمون به صورت زیر باشد:

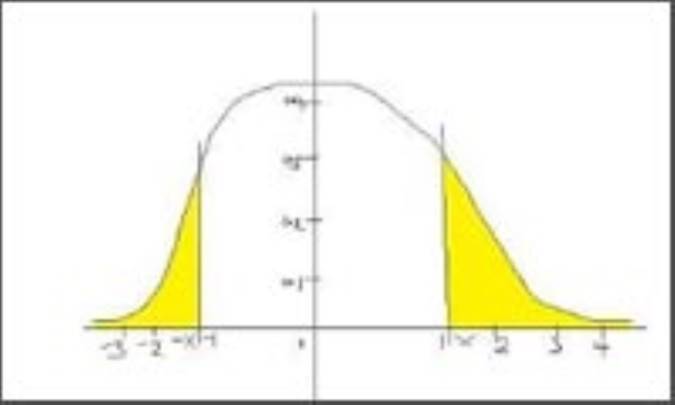
تفاوت یک آزمون یک طرفه با آزمون دو طرفه در شکل قابل مشاهده است. در مورد قبلی، تنها یکی از دو ناحیه رد (یا به اندازه کافی کوچک و یا به اندازه کافی بزرگ) مطابق با واقعیت فرضیه از پیش تعیین شده انتخاب می شود و آزمون تنها در مورد این معیار انجام می شود. هنگامی که شما یک منحنی زنگوله ای رسم می کنید، در واقع همان نمودار منحنی نرمال توزیع داده ها است. در این نمودار، داده ها در حالت افقی و موازی با محور X به صورت دو دنباله از داده قرار می گیرند. نام این آزمون هم به دلیل همین دنباله است.
(σ / √ n) / (μ - محاسبه میانگین (= ɀ
که در آن،
ɀ = آماره آزمون
μ = متوسط ارزش های آماره
σ = انحراف معیار استاندارد تفاوت بین تمام جفت ها
N = تعداد جفت
بنا بر این، با استفاده از این فرمول، می توان مثال زیر را برای درک بهتر این مفهوم آماری دنبال کرد.
 = 116
= 116
 => 116
=> 116
بنا بر این، با استفاده از سطح معنی داری 05ر0، مقدار بحرانی = 645ر1
از آنجا که، (σ / √ n) / (μ - محاسبه میانگین (= ɀ است،
از این رو، 34ر4=(150 √ / 3ر11) / (116-120)ɀ = .
می توان دید که، در منحنی زنگوله ای، آماره آزمون 34ر4 به سمت راست از مقدار بحرانی 1.645، در داخل منطقه بحرانی می باشد. بنا بر این فرضیه صفر رد می شود. هم چنین می توان از آزمون دو دامنه بالا نتیجه گرفت که فرضیه
صفر رد می شود. هم چنین می توان از آزمون دو دامنه بالا نتیجه گرفت که فرضیه  ، با استناد به مقدار متوسط بیشتر از 116 پذیرفته می شود. از این رو، استنباط آماری با بر آورد همکاران در تضاد است.
، با استناد به مقدار متوسط بیشتر از 116 پذیرفته می شود. از این رو، استنباط آماری با بر آورد همکاران در تضاد است.
آزمون دو طرفه
قبل از وارد شدن به جزئیات آزمون دو طرفه، اجازه دهید نگاهی گذرا بر استنباط آماری داشته باشیم. استنباط آماری اشاره به روند نتیجه گیری از یک مجموعه داده است که ممکن است بر تغییرات تصادفی، از قبیل تغییرات نمونه گیری و خطاهای مشاهده ای اثر داشته باشد. آزمون دو طرفه، آزمون آماری است که به نتیجه آماری می رسد. در این آزمون، فرضیه صفر H0، زمانی که مقدار آماره آزمون، که تابعی از نمونه است، به اندازه کافی کوچک و یا به اندازه کافی بزرگ باشد، رد می شود.در واقع ﻫﺮ ﺣﻜﻤﻲ درﺑﺎره ﺗﻮزﻳﻊ ﺟﺎﻣﻌﻪ ﻳﺎ ﭘﺎراﻣﺘﺮ ﺟﺎﻣﻌﻪ را ﻳﻚ ﻓﺮض آﻣﺎری می نامند و ﻣﻤﻜﻦ است درست یا نا درست باشد. درست یا نا درست بودن یک فرض، باید بر مبنای اطلاعات حاصل از نمونه گیری از جامعه بررسی شود. این عمل را آزمون فرض می نامیم. چون ادعا ممکن است درست یا نا درست باشد، بنا بر این دو فرض مکمل به وجود می آید: یکی برای آن که ادعا درست باشد و دیگری برای این که ادعا درست نباشد، بنا بر این شروع یک آزمون فرض، همواره شامل دو فرض آماری می باشد که در مقابل یک دیگر قرار می گیرند.
در ﺑﺤﺚ آزﻣﻮن ﻓﺮض اﻏﻠﺐ ﺑﺎ ﻓﺮض ﻫﺎ ﻳﺎ ادﻋﺎﻫﺎیی در ﻣﻮرد ﭘﺎراﻣﺘﺮﻫﺎی ﺗﻮزﻳﻊ ﺟﻮاﻣﻊ آماری مواجه هستیم. به این فرض یا ادعاها فرض صفر گفته می شود و آن را با
يك آزمون دو طرفه آزمونی است كه در آن فرض
تفاوت یک آزمون یک طرفه با آزمون دو طرفه در شکل قابل مشاهده است. در مورد قبلی، تنها یکی از دو ناحیه رد (یا به اندازه کافی کوچک و یا به اندازه کافی بزرگ) مطابق با واقعیت فرضیه از پیش تعیین شده انتخاب می شود و آزمون تنها در مورد این معیار انجام می شود. هنگامی که شما یک منحنی زنگوله ای رسم می کنید، در واقع همان نمودار منحنی نرمال توزیع داده ها است. در این نمودار، داده ها در حالت افقی و موازی با محور X به صورت دو دنباله از داده قرار می گیرند. نام این آزمون هم به دلیل همین دنباله است.
چه زمانی از این آزمون استفاده می شود؟
این آزمون برای استنباط آماری استفاده می شود، زمانی که فرضیه آماری به علت ارزش خود که یا به اندازه کافی بزرگ و یا به اندازه کافی کوچک است، رد می شود. به عبارت دیگر، زمانی که فرضیه صفر با توجه به ارزش خود در حال سقوط در هر یک از دو دامنه منحنی توزیع نمونه باشد، رد می شود. یک آزمون دو دامنه به منظور شناسایی تغییرات در پارامتر مورد استفاده قرار گرفته می شود.فرمول
فرمول استنباط آماری با استفاده از آزمون دو دامنه، به شرح زیر است:(σ / √ n) / (μ - محاسبه میانگین (= ɀ
که در آن،
ɀ = آماره آزمون
μ = متوسط ارزش های آماره
σ = انحراف معیار استاندارد تفاوت بین تمام جفت ها
N = تعداد جفت
بنا بر این، با استفاده از این فرمول، می توان مثال زیر را برای درک بهتر این مفهوم آماری دنبال کرد.
مسئله
در طول یک درایو استخدام، از 150 متقاضی کار، یک آزمون برای ارز یابی هوش (IQ) اخذ شد. از اطلاعات ارائه شده توسط متقاضیان، پرسنل استخدام متوجه شدند که میانگینIQ 120 است، و انحراف معیار نتایج 3ر11 است. آنها هم چنین تخمین زدند که متوسط جمعیت کمتر از 116 خواهد بود. با استفاده از سطح معنی داری 05ر0 تصمیم بگیرد که فرضیه درست است یا خیر.راه حل
بنا بر این، با استفاده از سطح معنی داری 05ر0، مقدار بحرانی = 645ر1
از آنجا که، (σ / √ n) / (μ - محاسبه میانگین (= ɀ است،
از این رو، 34ر4=(150 √ / 3ر11) / (116-120)ɀ = .
می توان دید که، در منحنی زنگوله ای، آماره آزمون 34ر4 به سمت راست از مقدار بحرانی 1.645، در داخل منطقه بحرانی می باشد. بنا بر این فرضیه
/م


























