ددکینت، (یولیوس ویلهلم) ریشارت

[(yulius vilhelm) riçārt dedekint]
(Julius Wilhelm) Richard Dedekind
(ت. برونسویک، آلمان، 13 مهر 1210 / 6 اکتبر 1831؛ و. برونسویک، 22 بهمن 1294 / 12 فوریه‌ی 1916)، ریاضیات.
نیاکان ددکینت (بویژه نیاکان مادری)، در خدمت به هانوْور و برونسویک، کسب امتیاز کرده بودند. پدرش، یولیوس لوین اولریش ددکینت، که پدر خودش پزشک و شیمیدان بود، حقوقدانی با درجه‌ی لیسانس، استاد، و وکیلِ دعاوی شخصیتی حقوقی درکولگیوم کارولینوم در برونسویک بود. مادرش، کارولینه ماری هنریئته امپریوس، دختر یکی از استادان کارولینوم و نوه‌ی یکی از رؤسای پُست امپراتوری بود. ریشارت ددکینت کوچکترینِ چهار فرزند خانواده بود. تنها برادرش، آدولف، به ریاست دادگاه بخشی در برونسویک رسید؛ یکی از خواهران، ماتیلده، در 1239 درگذشت، و ددکینت تا 1293 با خواهر دیگرش، یولیه، زیست، و هیچ یک از آن دو همسر اختیار نکرد. یولیه نویسنده‌ی مورد احترامی بود که در 1272 به دریافت جایزه‌ای محلی نایل آمد.
ددکینت از هفت تا شانزده سالگی در گومنازیوْم مارتینو کاتارینئوم در برونسویک تحصیل کرد. علاقه‌اش نخست متوجه شیمی و فیزیک بود؛ ریاضی را جز دانشی کمکی نمی‌دانست. اما دیری نکشید که در درجه‌ی اول به آن پرداخت، زیرا احساس کرد که فیزیک فاقد نظم و ساختاری دقیقاً منطقی است. در 1227 وی از دانشجویان کولگیوم کارولینوم شد، که مؤسسه‌ای علمی بین دبیرستان رسمی و دانشگاه بود، و کارل فریدریش گاوس هم در آن تحصیل کرده بود. در آن مؤسه ددکینت بر اصول هندسه تحلیلی، تحلیل جبری، حساب فاضل و جامع، و مکانیک عالی تسلط یافت، و به تحصیل علوم طبیعی هم پرداخت. در 1228-1229 به هانس تسینکه (معروف به زومر)، که بعداً در کارولینوم همکار او شد، درس خصوصی ریاضیات داد. بدین نحو، وقتی که در عید فسح 1850 (نیمه‌ی اول فروردین 1229) در دانشگاه گوتینگن ثبت نام کرد از بیشتر فارغ‌التحصیلان دبیرستان برای تحصیل آماده‌تر بود. درگوتینگن، به ابتکار موریتس آبراهام اشترن، مدرسه‌ای برای تربیت مدرس به منظور تدریس در آموزشگاهی تازه تأسیس شده بود. مدیریت بخش ریاضی برعهده‌ی اشترن و گئورگ اولریش بود، در حالی که ویلهلم وِبِر و یوهان بندیکت لیستینگ عهده‌دار اداره‌ی بخش فیزیک بودند. ددکینت از آغاز کار آموزشگاه عضو آن شد و در آنجا نخست با اصول نظریه‌ی عددها آشنا شد. یک سال بعد برنهارت ریمان هم شروع کرد به شرکت در آموزشگاه، و دیری نکشید که دوستی نزدیکی بین او و ددکینت استوار شد. در نخستین ششماهه‌ی ددکینت در درسهای حساب جامع و فاضل شرکت کرد و چیز قابلی نصیب او نشد. در درس آبگونه‌های (هیدرولیکِ) اولریش نیز حضور یافت اما بندرت در آزمایشگاههای فیزیک که وبر ولیستینک اداره‌شان می‌کردند شرکت می‌کرد؛ اما سخنرانیهای وبر درباره‌ی فیزیک تجربی در سراسر دو دوره‌ی ششماهه تأثیری نیرومند بر او بخشیدند. وبر اثری الهام‌بخش بر ددکینت گذاشت، و وی با تحسینی آمیخته به احترام به او پاسخ گفت. در نیمسال تابستانی 1229، ددکینت در درس اخترشناسی همه فهم که کارل وولفگانگ بنیامین گوتشمیت، راصد گاوس، می‌داد شرکت کرد؛ در نیمسال زمستانی 1229-1230، وی در درس و سخنرانی خود گاوس درباره‌ی روش کوچکترین مربعها حضور یافت. گاوس، با این‌که تدریس را خوش نداشت، کاری را که برعهده گرفته بود با همان وجدان ذاتی خود اجرا کرد؛ پنجاه ساله بعد ددکینت از این سخنرانی به عنوان یکی از زیباترین سخنرانیهائی که در عمر خود شنیده بود یاد می‌کرد: در این باره نوشته است که با علامتهای دم‌افزون به سخنان گاوس گوش فرا می‌داده و هرگز نتوانسته است تأثیری را که بر او گذاشته شده بود از یاد ببرد. در نیمسال بعدی، ددکینت سخنرانی گاوس درباره‌ی زمین‌سنجی پیشرفته را شنید. در ترم زمستانی 1230-1231 در سخنرانی کوئینتوس اتیسیلیوس را که درباره‌ی جغرافیای ریاضی و نظریه‌ی گرما ایراد شد شنید و در رصدهای هواشناختی اتیسیلیوس شرکت کرد. بعد از فقط چهار ترم تحصیلی، در 1231 کار دکتری خود را زیر نظر و به استادی گاوس، با پایاننامه‌ای درباره‌ی اصول نظریه‌ی انتگرالهای اوْیلری، آغاز کرد. گاوس تصدیق کرد که معلومات او زیاد، و وی مستقل است؛ علاوه بر این «انتظارهای مساعد از کار آینده‌ی او» پیش‌بینی کرد.
ددکینت بعداً به نحوی قاطع گفت که این معلومات برای دبیران دبیرستان کافی بوده اما برای پیش شرط‌های تحصیلات پیشرفته در گوتینگن کفایت نمی‌کرده است. مثلاً درباره‌ی این موضوعها هیچ سخنرانی نشنیده بود: گسترشهای تازه‌تر در هندسه، نظریه‌ی پیشرفته‌ی عددها، تقسیم دایره و جبر پیشرفته، تابعهای بیضوی، یا فیزیک ریاضی، که در آن زمان اشتاینر، یاکوبی و دیریکله در دانشگاه برلین تعلیم می‌دادند. پس ددکینت دو سال بعد از فراغ از تحصیل را با جدیت صرف پر کردن فضاهای تهی تحصیلات خود کرد – از جمله در دروس و سخنرانیهای اشترن درباره‌ی حل معادلات عددی حضور می‌یافت.
در تابستان 1233، چند هفته‌ای بعد از ریمان، صلاحیت ددکینت برای دانشیاری دانشگاه محرز شد. در ترم زمستانی 1233-1234 فعالیت تعلیماتی را با عنوان «معلم بی‌حقوق» (پریوات دوْتسنت)، با درسی از ریاضیات احتمالات و درس دیگری از هندسه، و به موازات آنها درباره‌ی هندسه‌ی تحلیلی و روشهای تصویری، آغاز کرد.
پس از آن‌که دیریکله در 1234 در گوتینگن جانشین گاوس شد، ددکینت در درسها و سخنرانیهای او درباره‌ی نظریه‌ی عددها، نظریه پوتانسیئل (عامل نهفته)، انتگرالهای معین، و معادله‌های دیفرانسیئل جزئی حاضر شد. دیری نکشید که رابطه‌ی شخصی نزدیکتری با دیریکله پیدا کرد و بحثهای بسیار بارور با وی داشت؛ ددکینت بعداً خاطر نشان ساخت که دیریکله از او «آدمی تازه» ساخته و افقهای درسی و شخصی او را وسعت بخشیده بود. وقتی که دیریکله و همسرش مهمانانی از برلین داشتند (بانو ربکا دیریکله خواهر فلیکس مندلسزون – بارتولدی، آهنگساز نامور، بود و تعداد زیادی دوست داشت)، ددکینت را هم دعوت کردند و او از محضر دلپذیر، مثلاً، کارل آوگوست فارنهاگن فون‌انزه، نویسنده‌ی نامی و سیاستمدار پیشین، و دختر خواهرش لوتمیلا آسینگ، که نیز نویسنده بود، برخوردار شد.
در ترم زمستانی 1234-1235 و ترم بعدی، ددکینت در دروس و سخنرانیهای ریمان درباره‌ی تابعهای بیضوی و آبلی حضور یافت. بدین نحو، با این‌که معلم بود، شاگردی ساعی هم باقی ماند. درسهای خودِ او در آن زمان از این حیث درخور ذکر است که وی شاید نخستین معلم دانشگاهی بود که درباره‌ی نظریه‌ی گالوا سخن می‌گفت، و در ضمن درسش مفهوم میدان نیز شناسانده می‌شد. مطمئناً تعداد دانشجویانی که در محضرش حضور می‌یافتند اندک بود؛ و وقتی که ددکینت از حدود گالوا فراتر رفت و به جای مفهوم گروه جایگشت مفهوم گروه مجرد را قرار داد تعداد حاضران فقط دو تن بود.
در 1237، ددکینت به پولی تکنیکوم زوریخ (حالا مدرسه‌ی عالی فنی کنفدراسیون سوئیس) دعوت شد تا جانشین یوزف لولویش رابه شود. بدین نحو ددکینت حلقه‌ی اول زنجیری دراز از ریاضیدانان آلمانی بود که زوریخ اولین منزلشان در راه وصول به یک کرسی درس حرفه‌ای آلمانی شد؛ و اینک نامهای اندکی از بسیار: ا. ب. کریستوفل، ه‍. آ. اشوارتس، گ. فروبنیوس، آ. هورویتس، ف. ا. پروم، ه‍. وبر، ف. شوتکی و ه‍. مینکوفسکی. مشاور مدرسه‌ی سوئیسی، که مسئول استخدام بود، دردم درباره‌ی ددکینت تصمیم گرفت – و این خود نشانه‌ای از توان تشخیص او است. در شهریور 1238، پس از آن‌که ریمان به عضویت مکاتبه‌ای فرهنگستان برلین برگزیده شد، ددکینت با او به آن شهر سفر کرد. در آنجا با مبتکر این گزینش، کارل وایرشتراس، و رهبران دیگر مکتب برلین، از جمله ارنست ادوئارت کومر، کارل ویلهلم بورشارت و لئوپولت کرونکر آشنا شد.

در 1241، به جانشینی آوگوست ویلهلم یولیوس اوده، در پولی تکنیکوم برونسویک، که از کولگیوم کارولینوم آفریده شده بود، منصوب شد. تا دم مرگ، در بستگی بسیار نزدیک با برادر و خواهرش، در برونسویک ماند و هرگونه امکان تغییر یا دستیابی به محیط کار فعالتری را نادیده گرفت. جهان خانوادگی کوچکی که وی در آن می‌زیست همه‌ی خواستهای او را کاملاً ارضا می‌کرد: در آن جهان بستگانش جانشین زن و فرزند خودش بودند و در آن از فراغ و آزادی کافی برای کار علمی در پژوهش بنیادین ریاضی برخوردار بود. هیچ علاقه‌ای به داشتن تأثیر بیشتر در جهان خارج احساس نمی‌کرد یا این گونه تأیید برای شخص خودش را لازم نمی‌شمرد.

هر چند به مسئولیت اداری بکلی بی‌میل بود، باز بر ذمه‌ی خود شمرد که از 1251 تا 1254 ریاست پوْلی تکنیکوم را عهده‌دار شود (تا حدّ زیادی او جانشین پدرش بود، که چندین سال عضویت اداره‌ی کولگیوم کارولینوم را داشت) و در جریان تبدیل مدرسه به دانشگاه فنی هیأت مأمور ساختمان مدرسه را سرپرستی کرد. جزء مسافرتهای تفریحی او به اتریش (تیرول)، سوئیس، و در جنگل سیاه (اشوارتس والت)، از دیدارش از نمایشگاه پاریس در 1257 نیز باید یاد کرد. در 12 فروردین 1273 با عنوان استاد ممتاز بازنشسته شد اما به سخنرانیهای گه‌گاهی ادامه داد. وی در 1251، بعد از درگذشت پدرش، بسختی بیمار شد، اما بعداً تندرستی خود را بازیافت و تا هشتاد و چهار سالگی که با آرامش درگذشت از سلامت تن و روان برخوردار بود.
ددکینت، که از 1241 عضو مکاتبه‌ای فرهنگستان گوتینگن بود، از 1259، به ابتکار کرونکر، عضو مکاتبه‌ای فرهنگستان برلین هم شد. در 1279 به عضویت مکاتبه‌ای فرهنگستان علوم پاریس درآمد و در 1289 به عضویت خارجی (associé étranger)‌آن فرهنگستان برگزیده شد. عضو «فرهنگستان عجایب طبیعی لئوپولدینو – کارولینا» و فرهنگستان رم نیز شد. درجه‌های دکتری افتخاری از دانشگاههای کریستیانیا (اوسلوی فعلی) و زوریخ و برونسویک گرفت. در 1281، به مناسبت پنجاهمین سالگرد دریافت درجه‌ی دکتری، افتخارات بسیار نصیب وی گردید.
ددکینت از ریاضیدانانی بود که استعداد موسیقی بسیار دارند. پیانو و ویولونسل را در حد کمال می‌نواخت، و یک اپرای مجلسی برای شعرهای اوپرای برادرش تنظیم کرد.
در سرشت و اصول، در اسلوب زندگی و نظرها و عقاید: ددکینت مشترکات بسیار با گاوس داشت، که او نیز از برونسویک برخاسته و در دبیرستان مارتینو کاتارینئوم و کولگیوم کارولینوم و دانشگاه گوتینگن تحصیل کرده بود. هر دو مرد احساسی محافظه‌کارانه، اراده‌ای انعطاف‌ناپذیر، و قدرت بی‌تزلزلی در برابر اصول داشتند، و از سازش سرباز می‌زدند. هر یک زندگی بسیارمنظم و ساده و عاری از تجمّل داشت. هر دو خونسردی و در داوری محتاط، آماده‌ی کمک به دیگران با دلی گرم، و دارای پیوندهای استوار بر اعتماد به دوستان خود بودند. هر دو دارای ذوق طنزی نمایان و در عین حال سختگیر نسبت به خود، و سخت با وجدان در انجام وظیفه بودند. بیزار از هر افراط‌کاری، هیچ یک برای جلوه‌گر ساختن احساس شگفتی یا تحسین شتاب نمی‌کرد. هر دو نسبت به نوآوریها بی‌میل بودند، و از قبول دعوتهای بسیار درخشان برای کرسیهای استادیِ جدید امتناع داشتند. هر دو والتر اسکات را جزء نویسندگان محبوب خود می‌مردند. هر دو خصلتی داشتند که می‌توان «بزرگی فروتنانه» اش خواند. پس جای شگفتی نیست که شباهتشان به ریاضی هم کشانیده شده باشد: ترجیح دادن نظریه‌ی عددها، محتاط بودن در مورد روشهای صوری و برتر شمردن «اصول» از «علائم». آن‌که تفاوتهای قابل ملاحظه و مهمی هم بین گاوس و ددکینت بود، جنبه‌ی آنچه مشترک می‌داشتند بسیار غالب بود. همانندی آنان جلوه‌ی خاصّ دیگری هم پیدا کرد: ددکینت از معدود برگزیدگانی بود که رخصت یافتند که تابوت گاوس را برای اجرای تشریفات بعد از مرگ به بام رصدخانه ببرند.
از گاوس که بگذریم، کسانی که بزرگترین تأثیرها را بر کار علمی ددکینت گذاشتند دیریلکه و ریمان بودند که ددکینت در گرایشها و نگرشهای متعدد با آنان سهیم بود. ددکینت، دیریلکه و ریمان، هر سه، به ارزش خود واقف بودند. اما، با تواضعی که به مرز حجب می‌رسید، هرگز نگذاشتند که همکارانشان به این امر پی ببرند. چون با جاه‌طلبی بیگانه بودند، وقتی که با درخشندگی و والایی ذهن و نیروی فکری خود روبرو می‌شدند دست و پای خود را گم می‌کردند. اندیشیدن را بیشتر از نوشتن دوست می‌داشتند و بزحمت یارای آن داشتند که خواستهای خود را ارضا کنند. چون در حدّ اعلای کمال بودند، درجه‌ی عشقشان به حقیقت ساده و روشن یکی بود. آنچه ددکینت خودش به تسینکه گفته بود از هر وصف دیگری که از او شود گویاتر است: «برای آنچه کرده‌ام و شده‌ام، باید خیلی بیشتر سپاسگزار حرفه‌ی خود، و کار خستگی ناپذیرم باشم و نه مدیون هنر برجسته‌ام».
وقتی که امروز نام ددکینت برده می‌شود، نخستین چیزی که تداعی می‌شود «بُرش ددکینت» است، که وی در 1251 وارد ریاضیات کرد تا در پرداختن به مسأله‌ی عددهای گنگ به نحوی کاملاً تازه و دقیق آن را بکار برد.
ددکینت، ضمن سخنرانیهائی که در 1237 در زوریخ در مورد حساب فاضل (دیفرانسیئل) می‌کرد، نبودن شالوده‌ای به معنی واقعی علمی برای حساب را خاطرنشان ساخت. (وایرشتراس هم ضمن تهیه‌ی سخنرانیهای خود از این گونه ملاحظات به پژوهشی دامنه‌دار و دوربُرد انگیخته شده بود.) در 2 آبان 1237، به بیان تعریفی صرفاً حسابی برای جوهر پیوستگی توفیق یافت و، در ارتباط با آن، بیانی دقیق از مفهوم عددهای گنگ بدست داد. چهارده سال بعد، نتیجه‌ی ملاحظات خود را در atetigkeit und irrational Zahlen («پیوستگی و عددهای گنگ»، برونسویک، 1882 و چاپهای بعدی) منتشر ساخت و عددهای حقیقی را به عنوان «برشهائی» در عددهای گویا شرح داد. وی به مفهومهائی با اهمیتی چشمگیر برای تجزیه‌ی عدد از طریق نظریه‌ی نظم دست یافت. خاصیت عددهای حقیقی، که وی آنها را به عنوان پیوستاری نظم‌دار در نظر گرفت، با کمکِ تصورّیِ برش که دوش به دوش آن حرکت می‌کند، یافتن ردّ عددهای حقیقی را در عددهای گویا میّسر ساخت: هر عدد گویای α تجزیه‌ی دستگاه R همه‌ی عددهای گویا را به دو رده‌ی A1 و A2 امکانپذیر می‌سازد به نحوی که هر عدد 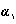عضو رده‌ی A1 از هر عدد 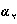عضو رده‌ی دوم A2 کوچکتر است. (امروزه اصطلاح «مجموعه» به جای اصطلاح «دستگاه» بکار برده می‌شود.) عدد a با بزرگترین عدد رده‌ی A1 است یا کوچکترین عدد رده‌ی A2. ددکینت تقسیم دستگاه R به دو رده‌ی A1 و A2 را به نحوی که 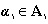هر از هر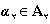 کوچکتر باشد، «برش» (A2 و A1) نامید. علاوه بر این، تعداد بیشماری برش وجود دارند که به وسیله‌ی عددهای گویا بوجود نیامده‌اند. ناپیوستگی برش وجود دارند که به وسیله‌ی عددهای گویا بوجود نیامده‌اند. ناپیوستگی یا ناکاملیِ ناحیه‌ی R عبارت از همین خاصیت است. ددکینت نوشت: «حالا، در هر موردی که برشی چون (A1 , A2) وجود داشته باشد که به وسیله‌ی هیچ عدد گویائی بوجود نیامده باشد، آنگاه ما عدد تازه‌ای «می‌آفرینیم»، عدد «گنگ» α، که آن را به وسیله‌ی این برش کاملاً تعریف شده می‌شماریم؛ خواهیم گفت که این عدد α متناظر است با این برش، یا این برش را بوجود آورده است» («پیوستگی و عددهای گنگ»، بند 4).
گاهی ددکینت را « ائودوکسوس نوین» می‌نامند، زیرا که بین نظریه‌ی عددهای گنگ ددکینت و تعریف متناسب بودن در نظریه تناسبهای ائودوکسوس [«اصول» اقلیدس، کتاب هفتم، تعریف 5] به شباهتی اثربخش اشاره شده است. با این همه، اوْسکار بِکِر بدرستی نشان داده است که نظریه‌ی برش ددکینت بر نظریه‌ی تناسبهای ائودوکسوس منطبق نمی‌شود: اصل موضوع ددکینت درباره‌ی وجود همه‌ی برشها و عددهای حقیقی‌ای که آنها را بوجود می‌آورند ممکن نیست در کار ائودوکسوس یا اقلیدس یافت شود. در این باره ددکینت گفته است که اصول اقلیدسی بتنهایی – بی‌آن‌که اصل پیوستگی، که در آنها نیست، به آنها علاوه شود – قادر نیست که نظریه‌ی کاملی برای عددهای حقیقی به عنوان تناسبهائی میان کمیتها بپروراند. اما، از سوی دیگر، به وسیله‌ی نظریه‌ی عددهای گنگ او نمونه‌ی کاملی از ناحیه‌ای پیوسته آفریده می‌شد که، درست به همین دلیل، می‌توانست هر تناسبی را به وسیله‌ی هر عددی که در آن بود مشخص سازد. [از نامه‌ای به رودوْلف لیپ شیتس، 12 مهر 1253].
ددکینت، با اثری که در 1251 منتشر ساخت، به صورت یکی از نمایندگان پیشرو عصر جدیدی از پژوهش، دوشادوش وایرشتراس و گئورگ کانتور، درآمد. این پژوهش دنباله‌ی کار کوْشی و گاوس و بولتسانو بود که به بیرون راندن ناروشنی از مفهومهای بنیادین به وسیله‌ی اثباتهای مبتنی بر سطح بالاتر صحت و دقت کمر بسته بودند. تعریف ددکینت و وایرشتراس از مفهوم بنیادین حساب، و نیز نظریه‌ی مجموعه‌های گئورگ کانتور، گسترش جدیدی را در ریاضیات موجب شدند که، به گفته‌ی داویت هیلبرت، «بیکباره زیر پرچم عدد قرار دارند».
کتاب Was sind und was sollen die Zahlen? («عددها چیستند و چه باید باشند؟») ددکینت (برونسویک، 1888، و چاپهای بعد) در همین خط سیر می‌کند: در آن وی نظریه‌ای منطقی برای عدد و استقرائی کامل عرضه کرد،‌ درک اصلی خود از جوهر حساب را نمایان ساخت، و به نقش دستگاه کامل عددهای حقیقی در هندسه در مسأله‌ی پیوستگی فضا پرداخت. کارهای دیگری هم کرد، از جمله برای متناهی بودن یا نامتناهی بودن مجموعه تعریفی کرد مستقل از مفهوم عدد، و به این منظور از مفهوم نگاشت (یا گسترش) استفاده کرد و تعریفی نابرگشتنی را که این همه برای نظریه‌ی عددهای ترتیبی مهم است بکار برد. (تصادفاً ددکینت عددهای ترتیبی و نه عددهای اصلی [Anzahl] را مفهوم ابتکاری و اصیل عدد می‌انگاشت؛ در عددهای اصلی فقط کاربردی از عددهای ترتیبی را می‌دید [نامه به هاینریش وبر، 4 بهمن 1267].) اثبات وجود تعداد نامتناهی از دستگاهها که ددکینت بدست داده بود همانند ملاحظه‌ای که بوْلتسانو در Paradoxien des Unendlichen («تناقضهای بی‌پایانها»، پراگ، 1851، بند 13») آورده بود دیگر اعتباری ندارد. کروْنکر حالتی انتقادی به خود گرفته بود از این که می‌دید ددکینت، با موافقت گاوس، در اعداد چون آفریده‌های آزاد فکر آدمی می‌نگرند و از این دیدگاه مبارزانه و با سماجت دفاع می‌کنند. وایرشتراس گلایه داشت که ددکینت تعریف او برای کمیتهای مختلط را خوب نفهمیده است. هیلبرت بر کوشش او برای آن‌که ریاضیات را فقط به وسیله‌ی منطق جایگزین سازد خرده می‌گرفت. گوتلوپ فرِگِه و برتراند راسل بر این رأی ددکینت خرده می‌گرفتند که برشها عددهای گنگ نیستند بلکه عددهای گنگ آنها را بوجود می‌آورند. با این همه، حق منتقدان او و آنان که راه و رسم کمتر انتزاعی کانتوْر برای ساختن عددهای حقیقی را بهتر می‌شمردند در این نکته همداستان بودند که وی تأثیری نیرومند بر پژوهش بنیادین ریاضی بخشیده است.
درست همان‌طور که کرونکر و وایرشتراس آثار ریاضی کسانی را که این دو خود را به آنان وامدار می‌دانستند ویراسته و برای چاپ آماده کرده بودند، ددکینت برای برپا ساختن بنائی ادبی برای کسانی که در کنارش ایستاده بودند کار کرد. در دسترس قراردادن کارهای گاوس و دیریکله و ریمان پس از درگذشت آنان جائی مهم در کارهای او دارد. با این کار مادی همذوقی و همفکری خود را ثابت کرد و نیز ترکیبی بس نادر از ترکیب هنرهای فکریِ تولید و دریافت خود را نمایان ساخت.
با منتشر ساختن دستنوشته‌های گاوس درباره‌ی نظریه‌ی اعداد (Werke) [«مجموعه آثار»]، جلد دوم [گوْتینگن، 1863]) نه تنها این فرصت مغتنم نصیب وی شد که نوشته‌های مردمی را که تا این حدّ زیاد مورد احترامش بود در دسترس محافل بزرگتری قرار دهد بلکه با تفاهم زیاد به شرح آنها نیز پرداخت. Vorlesungen über die Zahlentheorie («خواندنیهائی درباره‌ی نظریه‌ی عددها»)ی دیریکله (برونسویک، 1863، و چاپهای بعدی) با کوشش او به زینت طبع آراسته شد. اگر راست باشد که دیریکله اولین کسی بود که نه تنها Disquisitiones arithmeticae («پژوهشهای حسابی») گاوس را کاملاً فهمیده بلکه آنها را در دسترس دیگران نیز قرار داده بود، همین حکم تا حدّ زیادی بر روابط ددکینت با سخنرانیهای دیریکله درباره‌ی نظریه‌ی عددها جاری است. و آخر سخن، وی در ویرایش و چاپ Werke Bemhard Riemanns («آثار برنهارت ریمان»، لایپ تسیش، 1876؛ چاپ دومع 1892) با دوستش هاینریش وبر همکاری کرد و با همان فروتنی که خوی او بود اسمش را بعد از اسم وبر آورد.

چاپ سخنرانیهای دیریکله ددکینت را به بررسی ژرفی در نظریه‌ی عددهای مختلط تعمیم یافته، یا در صورتهائی که قابل تجزیه به عاملهای خطی باشند، کشانید. در 1250 این سخنرانیها را با ذیلی فراهم آورد که در آن نظریه‌ی میدانها، یا دامنه‌ها، عددهای جبری را جایگزین ساخت؛ برای این کار، تعریفی کلّی از مفهوم ایدئال کرد – و بسیار از نظریه «عددهای ایدئال» کومر فراتر رفت – و این تعریف در حوزه‌های گوناگون جبر و حساب ثمربخش بود. آنگاه ددکینت، مستقل از کرونکر و با تأیید او، چندین مقاله نوشته و نظریه‌ی ایدئالها را به نحوی پابرجا ساخت که شاهکار او انگاشته می‌شود. قضیه‌ی اصلی آن این بود که هر ایدئالی را که با واحد ایدئال R فرق داشته باشد می‌توان بی‌ابهام – جز در مورد ترتیب عاملها – به صورت حاصل ضرب عددهای اول نشان داد. ددکینت، در رساله هایش که مربوط به میدان عدد بود، به تعیین تعداد رده‌های ایدئال هر میدان توفیق یافت، در تحلیل مبنای میدان نفوذ کرد، مطالعات بخصوص درباره‌ی نظریه‌ی هنگ (مدُول)ها فراهم آورد، و موجب برانگیخته شدن گسترش بیشتری در نظریه‌ی ایدئالها شد که در آن امی نوْتر، هیلبرت، و فیلیپ فورت وِنگِلر شرکت کردند. پاول باخمان، آدوْلف هورویتس، و هاینریش وبر افکار ددکینت را در کتابهای خود منتشر ساخته آنها را بسط دادند.

گواه بر این‌که ددکینت از کاربردهای ریاضیات بکلی برکنار نبود رساله‌ای است که با. هِنبرک در 1230 منتشر ساخت، که مرتبط است با رابطه‌ی زمانی در شخم کشتزارهای با شکلهای گوناگون، و نیز تکمیل و انتشار رساله‌ای با دیریکله درباره‌ی مسأله‌ای مربوط به پویایی آبگونه‌ها (هیدرودینامیک) (1240).
کلام آخر، ما برای مفهومهای اساسی از قبیل «حلقه» و «واحد» مدیون ددکینت هستیم.
درباره‌ی احترام بزرگی که حتی در کشورهای بیگانه به ددکینت می‌گذاشتند قابل ذکر است که، پس از درگذشت او، و در گرماگرم جنگ جهانی اول، کامی ژوردان رئیس فرهنگستان علوم پاریس، نظریه‌ی عددهای صحیح جبری او را به عنوان کار اصلیش بگرمی ستود و از ضایعه‌ی فوت او ابراز تأسف کرد.
هر چند تداعی نام ریاضیدانان با مفهومها و قضیه‌ها همیشه از جنبه‌ی تاریخی توجیه‌پذیر و عموماً پذیرفته نیست، تعداد این گونه مفاهیم با ذکر نام ممکن است نشانه‌ای، هر چند نسبی، از کارهای پایدار ریاضیدان در بسط علم دانسته شود. با این محک، ددکینت متعلق به گروه بزرگترین ریاضیدانان است؛ نزدیک به دوازده مطلب ریاضی نام وی را بر خود دارند.

کتابشناسی

یکم. کارهای اصلی. برای دستیابی به فهرست نوشته‌های ددکینت، پوگندورف، یکم و 1863)، 534، 1555؛ سوم (1898)، 340، چهارم (1904)، 305؛ پنجم و 1926)، 269؛ و ششم (1936)، 538.
آثارش مشتملند بر: Gesammelte mathematische Werke، ویراسته‌ی ر. فریکه، ا. نوْتر، و ا. اوْره، 3 جلد (برونسویک، 1930-1932)، همراه با کتابشناسی در جلد سوم، 505-507؛ و Briefwechsel Cantor- Dedekind، ویراسته‌ی ا. نوتر و ژ. کاوایه (پاریس، 1937). گزیده‌هائی از آثارش در Die Grundlagen der Mathematik in Geschichtlicher Entwicklung، از اوسکار بکر (فرایبورک – مونیخ، چاپ دوم، 1964)، صفحات 224-245، 316، در دسترس است.
دوم. خواندنیهای فرعی. درباره‌ی ددکینت و آثارش، ـــــ «Richard Dedekind im Urteil der Berliner Akademie»، از کورت – ر. بیرمان، در FF، 40 (1966)، 301-302؛ «Richard Dedekind»، از اتمونت لانداو، در Nachrichen von der Königlichen Gesellschaft der Wissenschaften au Göttingen, Gesch äftliche Mitteilungen (1917)، 50-70، همراه با کتابشناسی در صفحات 66-70؛ Das Studium der Mathematik an den deutschen Universitäten seit Anfang des 19. Jahrhunderts، از ویلهلم لوْرای (لایپ تسیش –برلین، 1916)، همراه با مجموعه‌هائی خصوصی از ددکینت در صفحات 81-83؛ «Julie Dedekind»، از کارل مولنهاوئر، در BrM، 21 (1916)، 127-130؛ «Aus den Ahnentafeln deutscher Mathematiker: Richard Dedekind»، از ریچارد مولر، در FV، 4 (1955)، 143-145؛ «Richard Dedekind»، از نیکولاوس استولوف، در NDB، 3 (1957)، 552-553؛ «Erinnerungen an Richard Dedekind»، از هانس تسینکه («زومر»)، در BrM، 22 (1916)، 73-81؛ «Die Akademien zu Paris und Berlin über Richard Dedekind»، از همو، همان، 82-84؛ و «Julius Richard Dedekind»، از همو، در Festschrift zur Feier des 25-jährigen Bestehens des Gesellschaft ehemaliger Studierender des Eidgenössischen polytechnischen Schule in Zürich (1894)، 29-30.
منبع مقاله :
کولستون گیلیپسی، چارلز؛ (1387)، زندگینامه علمی دانشوران، ترجمه‌ی احمد آرام... [و دیگران]؛ زیرنظر احمد بیرشک، تهران: شرکت انتشارات علمی و فرهنگی، چاپ اول