درباره تنش و کرنش
قدرت یک ماده با نحوه پاسخگویی به تنش و کرنش اندازه گیری میشود. تنش، اندازهای است از نیروی داخلی در واحد سطح که بر روی جسم وارد میشود هنگامی که جسم تحت تأثیر نیروهای تغییر شکل دهنده قرار میگیرد. واحد تنش همان فشار است و برابر با نیوتن بر متر مربع است.از نظر مهندسی، کرنش با توجه به ابعاد اصلی آن، یک نسبت تغییر در ابعاد هر جسم است. این اعوجاج جسم است که بر اثر اعمال نیروهای خارجی بر روی آن اتفاق میافتد. این تغییر مکان لایههای جسم است که تحت تأثیر اِعمال نیروی تغییر شکل دهنده وارد بر ماده رخ میدهد.
قانون هوک رابطهای بین تنش و کرنش است که توسط یک جسمِ تحت دفرمه شدن احساس میشود. این قانونِ تقریبی بیان میکند که در حد الاستیک، کرنشی که توسط یک ماده احساس میشود مستقیماً با تنش متناسب است. حد الاستیک نقطهای است که اگر یک شیء فراتر از آن، کشیده شود، برای همیشه تغییر شکل میدهد. ضریب تناسب بین تنش و کرنش به عنوان مدول الاستیسیته ماده شناخته میشود.
تعریف
حد تناسب، حداکثر میزان تنش است که یک شیء میتواند تحمل کند در حالی که هنوز از قانون هوک پیروی میکند. به عبارت دیگر، بالاترین میزان تنشی است که ممکن است یک ماده در معرض آن قرار بگیرد در حالی که هنوز هم یک رابطه خطی با کرنش را حفظ میکند.اگر منحنی تنش را در برابر کرنش ترسیم کنید، خواهید دید که تا رسیدن به نقطه تسلیم، رابطهای خطی بین آنها وجود دارد. بعد از این مرحله، کرنش بدون افزایش تنش در حال افزایش خواهد بود. بالاترین مقدار تنش، درست قبل از رسیدن به نقطه تسلیم، به عنوان حد تناسب شناخته شده است.
اگر نیرویی اعمال کنید، فراتر از این حد، رابطه تناسب خطی بین تنش و کرنش دیگر حفظ نمیشود. اگر تنش بیشتری را فراتر از این مرحله اعمال کنید ممکن است مواد به طور دائمی تغییر شکل دهند. به خودی خود، هیچ فرمولی برای حد تناسب وجود ندارد، زیرا مقدار دقیق حداکثر تنش که یک ماده میتواند تحمل کند، کاملاً به ساختار مولکولی داخلی یا ساختار بلوری آن بستگی دارد.
اگر مهندسی تولید یا مکانیک را دنبال میکنید، میدانید که مطالعه خواص مواد مانند حد تناسب آنها و درجه بندی آنها با توجه به قدرت عملکرد آنها از مهمترین وظایف یک طراح و مدیر تولید است.
قانون هوک
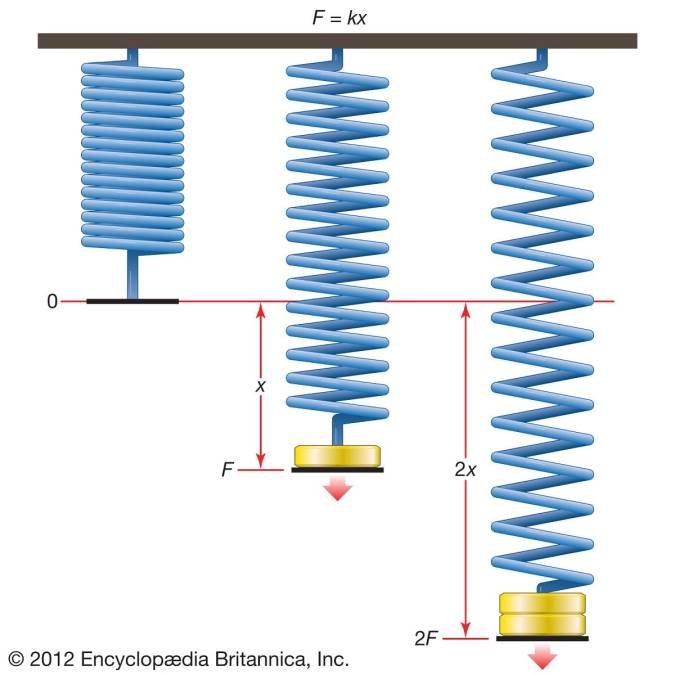
قانون هوک یک قانون فیزیکی است که میگوید نیرویی (F) که لازم است که فنری را به اندازه x بکشد یا فشرده سازد به صورت خطی متناسب با x است. یعنی Fs=kx که در آن k فاکتور ثابتی است که اندازه آن به ویژگی فنر مثل سختی آن بستگی دارد، و x در مقایسه با دفرمه شدن ممکن کلی فنر کمیت کوچکی است. این قانون به افتخار روبرت هوک، فیزیکدان انگلیسی قرن هفدهم به نام او نامگذاری شده است. وی برای اولین بار این قانون را در سال 1676 به صورت یک نمودار لاتینی بیان کرد.معادله هوک در بسیاری از مواقع دیگر که جسم الاستیک تحت نیروهای تغییر شکل دهنده قرار میگیرد، مانند مورد وزش باد بر روی یک ساختمان بلند، و یا زمانی که یک نوازنده رشتهی گیتار خود را میکشد، (تا حدی) اعتبار خود را حفظ میکند. به یک جسم یا مادهی الاستیکی که میتوان برای آن اعتبار این قانون را فرض کرد، خطی - الاستیک یا هوکیَن گفته میشود.
قانون هوک فقط یک تقریب خطی مرتبه اول به پاسخ واقعی فنرها و سایر اجسام الاستیک به نیروهای اعمال شده است. وقتی نیروهای اعمالی از حد مجاز فراتر رفتند این قانون درنهایت باید شکست بخورد، زیرا هیچ مادهای نمیتواند بیش از حداقل اندازه معینی فشرده شود، یا بیش از حداکثر اندازهای کشیده شود بدون این که تغییر شکل یا تغییر وضعیت دائمی بدهد. نمیتوان پیش بینی کرد که وقتی نیروهای بین مولکولی به ایفای نقش بپردازند ماده به صورت تودهای و بزرگ مقیاس چگونه رفتار خواهد کرد. حتی بسیاری از مواد به طرز محسوسی قبل از رسیدن به این محدودههای الاستیک، از قانون هوک کمابیش منحرف میشوند.
از طرف دیگر، قانون هوک تقریباً برای بسیاری از اجسام جامد یک تقریب دقیق است تا زمانی که نیروها و تغییر شکلها به اندازه کافی کوچک باشند. به همین دلیل، قانون هوک در همه شاخه های علوم و مهندسی بسیار مورد استفاده قرار میگیرد و پایه و اساس بسیاری از رشته ها مانند زلزله شناسی، مکانیک مولکولی و آکوستیک است. همچنین این قانون، اصلی اساسی در مقیاس فنر، مانومتر و چرخ تعادل ساعت مکانیکی است.
نظریه مدرن الاستیسیته، قانون هوک را تعمیم میدهد تا بگوید که کرنش (تغییر شکل) یک ماده یا ماده الاستیک متناسب با تنش اعمال شده بر آن است. با این حال، از آن جا که تنشها و فشارهای کلی ممکن است چندین مؤلفه مستقل داشته باشند، "ضریب تناسب" ممکن است دیگر فقط یک عدد واقعی واحد نباشد، بلکه یک نقشه خطی (یک تانسور) است که میتواند توسط یک ماتریس از اعداد حقیقی نشان داده شود.
در این شکل کلی، قانون هوک استنتاج رابطه بین کرنش و تنش را برای اشیاء پیچیده بر حسب خصوصیات ذاتی موادی که از آن ساخته شده است ممکن میسازد. به عنوان مثال، می توان نتیجه گرفت که یک میله همگن با سطح مقطع یکنواخت مانند کشش یک فنر ساده رفتار خواهد کرد با یک سفتی k که به طور مستقیم متناسب با سطح مقطع آن است و به طور معکوس متناسب با طول آن است.
منبع: اُمکار فاتاکک
























