

نویسنده: جمعی از نویسندگان
مقدمه
پیشرفت کامپیوتر از بزرگترین موفقیتهای فناوری محسوب میشود. اختراع کامپیوتر در ردیف استفاده از آتش، اختراع چرخ و مهار الکتریسیته قرار میگیرد. پیشرفتهای قبلی نیروهای اساسی را مهار کردند اما کامپیوتر اطلاعات خودش را مهار میکند.بیش از 90 درصد دانشمندانی که تاکنون روی کامپیوتر کار کردهاند هنوز زندهاند و کامپیوتر سرعت کارشان را هر روز افزونتر میکند. (نقشهبرداری از ژنهای انسان شاید تا نیم قرن زودتر از آن که پیشبینی میشد، تکمیل شد. برای این کار کامپیوتر به خدمت انسان آمده است).
اما بیش از حد نباید امیدوار بود. حدود 150 سال پیش از اختراع کامپیوتر امیدواریهای مشابهی با پیشرفت ماشین بخار توأم بود. طول عمر خطکش محاسبه کمتر از یک قرن است و این پیشرفت موجب بیکاری کامپیوتر میشود. که غیر قابل درک است چون تاکنون دربارهی آن فکری نشده است.
حتی پیش از آن که نخستین کامپیوتر ابداع شود، محدودیتهای تئوریک آن را میدانستیم. میدانستیم چه چیزی قابل محاسبه است. حتی وقتی که نخستین کامپیوترها ساخته شدند، کیفیت بالقوهی قدرت آن را درک میکردیم. کامپیوتر توانایی پردازش هوش مصنوعی را دارد. یک نفر مسئول هر دو ایده بود. نام او آلن تورینگ است.
تورینگ مردی غیرعادی بود که اندیشهی ساخت کامپیوتر به ذهنش خطور کرد. او روی ماشین حساب غولپیکری کار میکرد. این ماشین حساب در جنگ جهانی دوم راز معمای آلمانها را بر ملا کرد. تورینگ مانند ارشمیدس مجبور شد برای کمک به کشورش و حفظ آن برنامهی ریاضی جالبی را کنار بگذارد.
تورینگ بعد از مرگ نابهنگامش به فراموشی سپرده شد، اما امروزه احتمالاً چهرهی اصلی تاریخ کامپیوتر به حساب میآید.
دورهی پیش از تاریخ
کامپیوتر پیش از زمان حاضر
چرتکه، نخستین کامپیوتر بود. روش محاسبه با چرتکه حتی پیش از اختراع چرخ رایج بود. اسناد باستان شناسان تأیید میکند که حدود 4000 سال پیش از میلاد مسیح نوعی چرتکه در چین و خاورمیانه استفاده میشد. به نظر میرسد چرتکه در این دو منطقه ابداع شده باشد. برخی معتقدند اختراع چرتکه، آغاز رشد دانش ریاضی است چون نیاز مبرم برای محاسبه برای بشر غیر قابل اجتناب بود.چرتکه از کلمهای بابلی به معنی خاک گرفته شده است. از آن جا که تمام محاسبات روی خاک انجام میشدند، بنابراین خاک نام هر شکل محاسبه بود. به عبارت دیگر برای محاسبه با چرتکه خطوطی روی خاک میکشیدند. چرتکه به هیچ وجه جانشین دقیق کامپیوتر نیست، زیرا محاسبهی عملی را کسی انجام میداد که با چرتکه کار میکرد و برنامه محاسبه را در ذهن خود داشت.
چرتکه در قرون وسطی برای محاسبهی آسانتر در سراسر اروپا و آسیا استفاده میشد. سپس صفر وارد ریاضیات شد. در جایی که به چرتکه مربوط میشد، موانعی ایجاد شد. در نتیجه ریاضیدانهای جدی به سرعت این کمک کودکانه را حقیر شمردند. چرتکه تا قرنها بعد هم چنان وسیلهی محاسبه بود و هنوز هم نقش مهمی در اقتصاد محلی بخشهایی از آسیا و روسیه ایفا میکند.
قدیمیترین ماشین حساب شناخته شده در هالهای از رمز و راز قرار دارد. در سال 1900 میلادی غواصان جزیرهی کوچک انتیکترا در دریای اژه کشتی غرق شده مربوط به قرن اول میلادی را کشف کردند. آنها چند قطعه برنز زنگ زده را در بین مجسمهها و کوزههای شکسته پیدا کردند که به نظر میرسید قطعهای از یک ماشین باشد. پژوهشگران تا 50 سال بعد از آن میاندیشیدند که این قطعات چگونه با هم هماهنگ میشوند و یک دستگاه را میسازند. گونهای از ماشین حساب از قطعات مکانیکی برای محاسبه استفاده میشد. هندلی را باید بچرخانیم تا دندهها را به کار وا دارد، آنها هم شمارهگیرها را میچرخانند. بدین ترتیب خواندن موقعیت خورشید و سیارات در منطقه البروج امکانپذیر میشود.
این یک ماشین شگفتانگیز و بینظیر است. تاکنون هیچ چیزی مربوط به این دوره مانند این ماشین کشف نشده است. در ادبیات یونان باستان به چنین ماشینی یا چیزی مشابه آن اشارهای نشده است. هیچ فیلسوف، شاعر، ریاضیدان، دانشمند یا ستارهشناسی به چنین شیئی اشاره نکرده است. بر اساس یافتههای جدید ما، تخصص و تبحر تولید چنین ماشینی در یونان باستان وجود نداشت. نخستین کامپیوتر دستگاهی عجیب مانند اسباببازی بود که برخی نوابغ ناشناختهی مکانیک آن را ساخته بودند. این دستگاه عجیب مانند ستارهی دنبالهدار بدون تأثیرگذاری در تاریخ محو شد. سپس برای بیش از هزار و پانصد سال چیزی وجود نداشته است.
ویلیام شیکارد استان زبان عبری دانشگاه توبینگن در سال 1623 میلادی نخستین ماشین حساب مکانیکی واقعی را ساخت. شیکارد دوست یوهانس کپلر، اخترشناس بود. کپلر قوانین حرکت سیارات را کشف کرد. او علاقهی ذاتی استان زبان عبری را به ریاضیات و محاسبه که طی سالها کمی رنگ باخته بود، برانگیخت. شیکارد تصمیم گرفت ماشینی بسازد که در جمع زدن به او کمک کند. ماشین شیکارد را ساعت حسابگر توصیف کردهاند. این ساعت برای کمک به ستارهشناسان طراحی شده بود و به آنها کمک میکرد تا مکان ستارهها و موقعیت آیندهی خورشید، ماه و سیارات را بیابند. متأسفانه نمیدانیم که آیا این ماشین کار میکرد یا دقیقاً چگونه طراحی شده بود تا کار کند. نخستین و تنها نمونه، ناقص بود. آتش جنگهای سیساله، طرح شیکارد را نابود کرد. شیکارد به جای ایفای نقش در مقام مخترع مهمترین پیشرفت علمی، صنعتی از زمان اهلی کردن حیوانات، به نوشتن یادداشتی تاریخی بسنده کرد.
اکنون میدانیم که ماشین شیکارد مدل قدیمی کامپیوترهای دیجیتال بود که دادههای آن شکلی از اعداد بود. برای انواع دیگر کامپیوترها و مثلاً کامپیوتر آنالوگ؛ اعداد دادهها (وستاندهها) با مقادیر قابل اندازهگیری از قبیل ولتاژ، وزن یا طول جایگزین میشوند. آخرین نمونه از اینها در نخستین کامپیوتر آنالوگ، خطکش محاسبه به کار رفت که در دههی 1630 میلادی اختراع شد. سادهترین خطکش محاسبه شامل دو خطکش بود که با مقیاسهای لگاریتم شمارهگذاری شده بود. با تنظیم خطکشها برای جایگزین کردن یک عدد در برابر دیگری، به سادگی میتوانیم ضرب و تقسیم را بخوانیم.
خطکش محاسبه را ویلیام اوترد کشیش اختراع کرد. پدر او در اتون کاتب و دبیر بود و به بچههای بیسواد خواندن و نوشتن میآموخت. ویلیام اوترد نخستین خطکش محاسبهی مستقیم را در دههی 1630 میلادی تولید کرد (دو خطکش مستقیم) چند سال بعد هم ایدهی خطکش محاسبهی دایرهای را مطرح کرد که به جای خطکش محاسبه، دایرهای متحرک درون حلقه داشت. متأسفانه یکی از دانشآموزان اوترد این ایده را ربود و منتشر کرد و ادعا نمود که این کشف او است. اوترد از این موضوع ناخشنود شد، اما باید به روزهای خوش یک نفر پایان داده شود. گفتهاند او سلطنت طلبی وفادار بود که به خاطر شنیدن این که چارلز دوم دوباره بر تخت سلطنت نشسته، از فرط خوشحالی مرده است.
خطکش محاسبهی اولیه طی سالها تکمیل شد و به ابزاری برای محاسبات پیشرفته تبدیل شد. جیمز وات یکی از کسانی بود که در تکمیل این خطکش مشارکت داشت. او برای محاسبهی طرح اولیهی ماشین بخار در دههی 1780 میلادی از خطکش محاسبه استفاده کرد. پیشرفت بعدی خطکش محاسبه را امادی منهایم، افسر توپخانهی ارتش فرانسه انجام داد. امادی نوعی خطکش محاسبه طراحی کرد که یک دانشجو هم میتوانست در امتحانات بزرگ مربوط به آموزش نظامی نتایج خوبی از آن به دست آورد. خطکش محاسبهی مانهایم در نیمهی اول قرن بیستم مورد استفادههای فراوانی قرار گرفت.
پیشرفت بعدی در این حوزه متعلق به بلز پاسکال، ریاضی دان فرانسوی قرن هفدهم است. پاسکال در سال 1623 میلادی، درست همان سالی که شیکارد ساعت محاسبهی اولیه را اختراع کرد، به دنیا آمد. پدر پاسکال مأمور وصول مالیات سلطنتی بود که برای وجوه نقد دچار دشواری زیادی میشد. لذا به فرزندش اجازه داد تا به محاسبات ضروری خزانهداری سلطنتی رسیدگی کند. پاسکال، این جوان گران قدر برای کمک به پدرش طراحی ماشین حساب را شروع کرد. او در سن 19 سالگی مدل کاری برای ماشین حساب تولید کرد. اعداد با چرخ شمارهگیری وارد ماشین میشد، چرخها با چرخ دنده و دندانهها به میلهای وصل میشد. ماشین پاسکال میتوانست تا هشت رقم را جمع و تفریق کند. برای ساخت این ماشین فوقالعاده پیچیده به نهایت فنون مکانیکی و گاهی حتی به فراتر از آن نیاز بود. مشکل این ماشین، دندانههای آن بود اما پاسکال که شخصی کمالگرا بود، ادعا میکرد بیش از 50 مدل متفاوت ساخته است. پاسکال نه تنها ریاضیدانی بزرگ، بلکه بهترین فیلسوف مذهبی دوران خودش هم بود. او از بیماری رنج میبرد و تعصب مذهبی فزایندهی او به طور معکوس با سلامتیاش پیش میرفت. پاسکال تا آخر عمرش ریاضیدان باقی ماند. در حالی که ایمان او به احتمالات ریاضی کاهش یافت. به نظر او در حالی که انسان میتواند دربارهی وجود خدا از احتمالات استفاده کند، بهتر است احتمال بدهد که خدا وجود دارد.
هفت عدد از ماشینهای پاسکال هنوز وجود دارند، شاهکارهایی که چند اصل را شامل میشوند و هنوز هم در کامپیوترهای مکانیکی به کار میروند.
پیشرفت مهم بعدی در کامپیوترهای دیجیتال مرهون تلاش فیلسوف آلمانی، گوتفرید لایب نیتز است که لئوناردو داوینچی زمان خودش بود. طراحی برنامهی مفصلی برای حمله به مصر، تألیف تاریخ 15 جلدی خاندان هانوور و ساخت ماشین حسابی پیشرفتهتر از ماشین حساب پاسکال، از جمله کارهای او بود.
علاقهی لایب نیتز به ماشین حساب بیش از پاسکال بود. او در مقالهای مبانی نظری حسابگرها و کاری را که میتوانند انجام دهند، توضیح داد. (کاری که حدود 300 سال بعد به ایدهی تورینگ دربارهی این موضوع رهنمون شد.) درهمان زمان که ریاضی دوتایی را اختراع کرد، از قبیل همان چیزی که باید زبان کامپیوترهای دیجیتال شود، با این حال او هر دو را با هم ترکیب نکرد.
لایب نیتز پس از آن که یکی از ماشینهای حساب پاسکال را در پاریس دید، در سال 1673 میلادی ماشین حساب خودش را تولید کرد. متأسفانه لایب نیتز در آن زمان ورشکست شد و تلاشهای او برای تولید ماشین حسابی که از نظر تجاری ارزشمند باشد، بینتیجه ماند. (ماشین حساب پاسکال پیچیدهتر از آن بود که کس دیگری بتواند آن را تولید کند.) زمانی که لایب نیتز ماشین حساب خود را ساخت، از عرض دریای مانش گذشت تا آن را به انجمن سلطنتی لندن نشان دهد. اعضای انجمن سلطنتی علاقهای نشان ندادند و او این پروژوه را در مراحل اولیه رها کرد.
علیرغم این محدودیتها ماشین لایب نیتز قابل توجه بود و مانند ماشین حساب پاسکال با چند دندهی متوالی کار میکرد. اما توانایی آن از ماشین حساب پاسکال بیشتر بود. ماشین لایب نیتز از همان ابتدا میتوانست عمل ضرب و جمعهای متوالی را انجام دهد اما او به زودی ابزارهایی ساخت که آن ماشین حساب میتوانست عمل تقسیم را هم انجام دهد و جذر را محاسبه کند.
لایب نیتز آیندهی روشنی برای ماشین حساب میدید، در حالی که بعد از آن هرگز وقت نداشت تا در این زمینه عملاً تلاش کند. البته ذهن فعال او از کار روی ماشین حساب و نقشی که در آیندهی جهان ایفا خواهد کرد باز نایستاد. او معتقد بود روزی همهی مباحث اخلاقی با ماشین حساب قابل توضیح خواهد شد و ماشین به انسان خواهد گفت که کدام بحث ارزشمندتر است. در حالی که مبنای دقیق این محاسبات مانند مقولهی محاسبهی احتمالات قبلی بود. این مطلب جز برای نوابغ که آن را درک میکردند، برای بقیه در هالهای از رمز و راز بود.
لایب نیتز پیشبینی کرد که ماشینهای حساب به زودی جای قاضیها را خواهند گرفت و دادگاههای قانونی آینده با ماشین حساب اداره خواهد شد. ماشین حساب خواهد توانست رأی دهد و مجازات مناسب را ارائه کند. چنین پیشگویی شگفتانگیزی ممکن است ترسناکترین داستان کامپیوتر را یادآوری کند، اما لایب نیتز آن را طور دیگری میدید، او اصولاً شخصی خوشبین بود و عقیده داشت که همه چیز در مساعدترین شرایط امکان بهترین شدن دارند. چنانچه او انرژی استثناییاش را بیشتر صرف تولید ماشین حساب میکرد، ضرورت نداشت تا بگوید ماشین حساب احتمالاً چه دنیایی ایجاد میکند.
پیشرفت مهم بعدی را در این زمینه شخصی کاملاً بیگانه به این موضوع انجام داد. جوزف ماری ژاکارد، تکنیسین فرانسوی بود که در حرفهی بافندگی فعالیت میکرد. او دستگاه پارچه بافی ابتکاری خودش را اوایل قرن بیستم، در جایی که طرح بافندگی با کارت پانچ کنترل میشد نصب کرد. با این کار ایدهی برنامهریزی ماشینی طراحی و اجرا شد اما ژاکارد از اهمیت اختراعش اطلاعی نداشت. ماشینهای او در دههی 1820 میلادی سبب شورشهایی شد و کارگران بافندی به کارخانهها حمله کردند و بسیاری از ماشینها منهدم شدند. روش ژاکارد اکنون هم برای یافتن طرحهای پیچیده به کار میرود.
عناصر اصلی کامپیوترهای بزرگ یعنی ماشین حسابهای مکانیکی پیچیده ایدهی برنامهریزی و نظریهی اعداد قابل محاسبه، شروع به پیدایش کردند. اما به هوش فوقالعاده نیاز بود تا مشخص شود که این عناصر متفاوت چگونه با هم ترکیب میشوند.
چارلز ببیج را به عنوان پدر کامپیوتر میشناسند. او هم مانند بسیاری از نوابغ در حوزهی عملی، ناکارآمد بود اما کشفیات و موفقیتهای او یک قرن از خودش جلوتر بود.
ببیج در سال 1791 میلادی به دنیا آمد. او ثروت قابل ملاحظهای را به ارث برد و به زودی استعداد درخشان خود را در ریاضیات نشان داد. ببیج برای معرفی دستگاه علامتگذاری حساب لایبنیتز در بریتانیا تلاش کرد. (ریاضیدانان بریتانیا از روی وطنپرستی بر استفاده از دستگاه علامتگذاری قدیمی نیوتن اصرار میورزیدند، اما با این کار خودشان را یک قرن از پیشرفتهای قارهی اروپا محروم کردند.)
مسائلی که دانشمندان بریتانیا را به شکل قابل ملاحظهای از پیشرفت محروم میکرد، توجه ببیج را به خود جلب کرد. آنها اشتباهاتی بودند که در کتب ستارهشناسی و جداول ریاضی به چشم میخوردند. مثلاً نخستین چاپ کتاب «جدول دریانوردی برای یافتن طول و عرض جغرافیایی در دریا» شامل هزار اشتباه بود!
ببیج فکر کرد که تنها یک جواب برای مشکل جداول غلط وجود دارد. به نظر او به ماشین حساب بزرگ، همه کاره و مطمئن نیاز بود. ببیج ساخت موتور معروف تفاضل شماره 1 را شروع کرد و پس از استفادهی موفقیتآمیز برای مقاصد دولتی در نظر گرفت. این مسئولیتی فوقالعاده بزرگ و بلندپروازانه بود. ماشین حساب ببیج میتوانست تا 20 رقم را محاسبه کند، سریهای اعداد را ذخیره کرده و آن اعداد را جمع کند. محاسبات این ماشین به عمل جمع محدود میشد، چون روش تفاضلهای متعدد را به کار میبرد. از فرمول چند جملهای (فرمول جبر شامل چند جمله است) و این حقیقت که آنها مقدار ثابت دارند استفاده میکنیم و آن را به سادهترین شکل مینویسیم:
در حالی که:
F(x)=2X+1
X=1 2 3 4 …
F(X)=3 5 7 9 …
...2 2 2 2 = تفاضلها
نیازی به گفتن نیست که در مورد مسائل پیچیده چندان آسان نیست. اما تفاضل ثابتی بین تفاضلها پیدا میشود (یا تفاضلهای بین تفاضلهای بین تفاضلها). در بیشتر موارد اگر چند جملهای جملهی
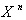 داشته باشد، آن گاه n تفاضل باید پیش از تفاضل ثابت محاسبه شود. برای حل کردن چند جملهای برای توالی مقادیرX همان طور که برای محاسبهی جدولها لازم است، برای ماشین آسان است تا به جای آن که سریهای پیچیدهی عمل ضرب را محاسبه کند، ماندههای ثابت را جمع ببندد و سپس ماندهها را مجدداً جمع بزند. که در تابعهایی مانند لگاریتم و مثلثات کاربرد دارند.
داشته باشد، آن گاه n تفاضل باید پیش از تفاضل ثابت محاسبه شود. برای حل کردن چند جملهای برای توالی مقادیرX همان طور که برای محاسبهی جدولها لازم است، برای ماشین آسان است تا به جای آن که سریهای پیچیدهی عمل ضرب را محاسبه کند، ماندههای ثابت را جمع ببندد و سپس ماندهها را مجدداً جمع بزند. که در تابعهایی مانند لگاریتم و مثلثات کاربرد دارند.موتور تفاضل شماره 1، مانند اسلاف خود از چرخهای دندانهدار استفاده میکرد و بر اساس سیستم اعشاری عمل میکرد اما ساختار آن تا حد وسیعی پیچیدهتر از بقیه بود چون برای ساخت آن به توالی ابداعات در مهندسی مکانیک نیاز است.
ببیج هم در این کار خوش درخشید. او در گذشته معلم بود و ماشین خود را با عجله ساخته بود. اما به مرور زمان ایدههای درخشانی برای کارهای ابتکاری به ذهنش رسید و آنها را به منصهی ظهور رسانید. ساخت موتور تفاضل شمارهی 1 در سال 1823 میلادی شروع شد، اما هرگز تکمیل نشد. ببیج پس از ده سال کار، طرح اولیه را به ماشینی با 25000 قطعه گسترش داد در حالی که فقط 12000 قطعه از آن ساخته شده بود. هزینهی ساخت این ماشین 17470 پوند برآورد شده بود. این پول در آن زمان برای ساخت دو فروند کشتی جنگی کافی بود. ببیج مقادیر زیادی از جیب خودش پرداخت، اما دولت تصمیم گرفت تا این طرح را متوقف کند. به نظر دولت بهتر است تا در کشتی سازی سرمایهگذاری کنیم تا در ماشینی که بدون آن هم میشود محاسبه کرد. علیرغم این مشکلات ببیج در سال 1827 میلادی تنها یک بخش از ماشینش را به کار انداخته بود که جدول لگاریتم از 1 تا 108000 را محاسبه میکرد. این بخش از ماشین شامل 2000 قطعه بود و اولین ماشین حساب خودکار محسوب میشد. ارقام را وارد ماشین حساب میکردند و جوابها به شکل چاپ شده بیرون میآمد بنابراین احتمال اشتباه انسانی از بین میرفت.
اما این شروع کار بود و ببیج نگران بود. او در دههی 1830 میلادی طرحهایی برای ساختن موتور تفاضل شمارهی 2 در نظر داشت. موتور تفاضل شماره 2 پیشرفت بزرگی در روشهای محاسبه و نخستین ماشین تجزیه و تحلیل بود، ماشینی که برنامهای خارجی کار آن را کنترل میکرد. خبر ایدهی کارتهای پانچ ژاکارد برای کنترل مکانیسم ماشین به گوش ببیج رسیده بود و لذا تصمیم گرفت این ایده را در ماشین خودش به کار برد. بدین ترتیب ماشین امکان مییافت تا طبق دستورات ارائه شده از کارتها با سوراخهایی که در آن پانچ شده بود، محاسبات مختلف را اجرا کند. این ماشین هم مانند نخستین موتور تفاضل برای نگهداری اعداد حافظه داشت، اما ماشین جدید میتوانست ترتیبی از عملیات شامل اعداد ذخیره شده را انجام دهد. ببیج ویژگیهای اصلی کامپیوترهای امروزی را پیشنهاد کرده بود.
پردازشگر مرکزی با این ویژگیها یک شاهکار بود. این قسمت باید شامل هزار میلهی وردنه با حدود 50000 چرخ دنده باشد تا بتواند اعداد 50 رقمی را با استفاده از سیستم اعشاری محاسبه کند.
سالها کار سخت و بینتیجه تأثیر مخربی بر شخصیت ببیج داشت. مرد جوان و خوشقیافهی کمبریج به پیرمردی تندخو تبدیل شده بود که در خیابانهای لندن سرگردان بود. او دیوانهی موسیقی نوازندگان خیابانی بود که بچههای فقیر و ژندهپوش را به شادی وا میداشت. آدمهایی که گاهی با صدایی نخراشیده با آنها همراهی میکردند... دستهی دیگری از حامیان موسیقی خیابانی شامل افرادی با اخلاقیات و تمایلات جهان وطنی بودند. ببیج تصمیم گرفته بود تا مانع از کار نوازدگان خیابانی شود و ادعا میکرد که آنها نمیگذارند در آرامش کار کند. نوازندگان خیابانی هم با تجمع جلوی پنجرهی خانهاش در صدد انتقام گرفتن از او بودند. ببیج نوشته که در یک موقعیت سازهای برنجی، با وقفهی کوتاهی به مدت پنج ساعت شروع به نواختن میکنند.
ببیج در آن زمان بیشتر ثروت شخصیاش را برای به تحقق رساندن رویای موتور تفاضل خرج میکرد. خانم ادا لاولیس از بهترین زنان ریاضیدان زمان خودش نیز در این تلاشها به ببیج کمک میکرد. تأثیر او در تاریخ کامپیوتر سبب شد تا وزارت دفاع ایالات متحدهی آمریکا از او قدردانی ویژهای بکند و نام ادا را بر زبان برنامهنویسیاش بگذارد. بانولاولیس در تلاش خوشبینانهی ببیج برای بازیابی ثروتش هم به او کمک کرد. آنها وقت و انرژی خود را صرف ساختن دستگاه بدون خطای شرطبندی برای مسابقهی اسب دوانی کردند اما در حین آزمایشات عملی روشن شد که این دستگاه تقریباً همان موتور تفاضل است.
علی رغم چنین اتفاقاتی ببیج فرصت یافت تا سپر لوکوموتیو را اختراع کند و کشف کرد که چگونه از سه حلقه برای ثبت آب و هوا میتوان استفاده کرد. پس از آن که ببیج در سال 1871 میلادی مرد، طرحهای او برای ساخت موتور تفاضل شماره 2 سالهای زیادی به بوتهی فراموشی سپرده شد. متعاقب آن دستگاه نورد نخستین موتور تحلیلگر برطبق طرحهای اصلاح شده برای موتور تفاضل شماره 2 ساخته شد. این ساختمان سه تنی با عظمت را امروزه میتوانید با همهی جلال و شکوهش در موزهی علوم لندن ببینید. اما این کار دستگاه چه بود. در آزمایشات برای محاسبهی 25 ضربدر عدد پی تا 29 رقم اعشار بود، یعنی کاری که 50000 چرخ دنده دستگاه به راحتی آن را انجام میدهند.
ببیج مشخصات اصلی کامپیوترهای جدید را طراحی کرد، اما ماشین او دچار نقص مهمی بود. دستگاه ببیج با ریاضیات ده دهی کار میکرد و این نقص باید اصلاح میشد. جرج بول از معاصرین ببیج این نقص را اصلاح کرد. جرج بول فرزند لینکلن کابلر در سال 1813 میلادی متولد شد. او تحصیلات کلاسیک نداشت اما استعداد خود را نشان داد، به طوری که به سمت استادی ریاضیات در کین کالج کورک منصوب شد. او با مری اورست دختر خواهر مردی که نامش بر قلهی اورست نهاده شد، ازدواج کرد.
بول در سال 1854 میلادی «بررسی قوانین اندیشه» را منتشر کرد، چیزی که امروزه به نام جبر بول شناخته شده است. بول در اثرش بیان میکند که منطق هم شکلی از ریاضیات است. منطق هم مانند مثلثات بر مبنای موضوع سادهای بنا گذاشته شده است. در جایی که ریاضیات کارهای اولیه مانند تقسیم را انجام میدهد، منطق را هم میتوان تا حد کلماتی مانند «و»، «یا»، «نه» ساده کرد. این عملیات را میتوان در دستگاه دوتایی به کار برد. (درحالی که در دستگاه ده دهی ده رقم دارد، دستگاه دوتایی به همان شکل با دو رقم کار میکند.) «درست» و «نادرست» منطق را میتوان به 0 و 1 تبدیل کرد. جبر دوتایی هر مطلب منطقی را میشکند و به ترتیبی از نمادهای دوتایی تبدیل میکند، مهم نیست که چند تا جمله در آن به کار رفته باشد. آن را میتوان روی نواری از کاغذ نوشت، در حالی که جبر دوتایی به ترتیبی از سوراخها تبدیل میشود. بدین ترتیب یک برنامهی کاملاً منطقی را به راحتی میتوان به ماشین ارائه کرد.
ماشینها با ارقام دوتایی میتوانند دستورات منطقی را اجرا کنند و ریاضیات این ماشینها هم کاملاً بر مدارهای خاموش و روشن الکتریکی منطبق است. در نتیجه ارقام دوتایی (بیت) سرانجام به واحد سازندهی اطلاعات در دستگاه کامپیوتر تبدیل میشود. اما در زمان حاضر پیشرفتهای جداگانهی ببیج و بول ناشناخته مانده است.
پیشرفت مهم بعدی مدیون یک آمریکایی متخصص آمار به نام هرمان هولریس است. هولریس ماشین سرشماری را توسعه داد، به طوری که میتوانست کارتهایی با 288 سوراخ را بخواند و اطلاعات را در آنها ذخیره کند. ماشین الکترومکانیکی او میتوانست تا 80 کارت را در دقیقه بخواند. در سال 1890 میلادی از دستگاه هولریس برای سرشماری استفاده شد و این دستگاه ظرف مدت شش هفته اطلاعات را پردازش کرد. (سرشماری قبلی در سال 1880 میلادی سه سال طول کشیده بود). هولریس در سال 1896 میلادی، وارد تجارت شد و شرکت ماشینهای فهرست گذاری را تأسیس کرد. بعدها نام آن به شرکت بینالمللی ماشینهای تجاری (IBM) تغییر کرد.
عناصر ضروری برای کامپیوترهای جدید (شامل بهرهبرداری بازرگانی) طراحی شده بودند اما باید کسی پیدا شود که بداند این عناصر چه کارهایی میتوانند انجام دهند. یعنی احتمالات نظری و محدودیتهای آن را بشناسد، این کار را آلن تورینگ انجام داد.
رمز و راز زندگی تورینگ
آلن تورینگ در سال 1912 میلادی در خانوادهای از طبقهی متوسط انگلیس در لندن به دنیا آمد. پدر او در خدمات شهری هند کار میکرد و مادرش دختر سرمهندس راه آهن مدرس بود. والدین او در سال 1913 میلادی به هند برگشتند و آلن و برادر پنج سالهش را تحت قیومیت سرهنگی بازنشسته و همسرش در ست لئونارد کنار دریای ساسکس قرار دادند.در آن روزگار والدین انگلیسی به محدود کردن بچههایشان به شکل امروزی نمیاندیشیدند. حتی آنهایی که نمیخواستند بچهها را به مستعمرات ببرند، برای بچهها دایه میگرفتند یا آنها را از سن هفت سالگی به مدارس شبانه روزی میسپردند. آن نوع از زندگی روی جان، برادر آلن تأثیر گذاشت و او همهی خصوصیات بچههای معمولی انگلیسی را کسب کرد. اما آلن از نظر عاطفی ضربه خورد و دچار لکنت زبان شد. او خود را در رعایت آداب و رسوم زندگی اجتماعی ناتوان میدید.
وقتی مادر آلن برای دیداری طولانی در سال 1916 میلادی به وطن برگشت و آلن جوان متوجه شد که برای بقیهی عمرش در کنار او زندگی خواهد کرد، با احساساتی متضاد واکنش نشان داد. او از صمیم قلب مادرش را دوست داشت، اما او را غیر قابل تحمل یافت. به نظر میرسید خانم تورینگ هم دربارهی آلن چنین عقیدهای داشت. تنها نگرانی مادر این بود که آلن به شخصی قابل احترام تبدیل شود اما بچه شیطان درون او آن را غیرممکن کرده بود.
آلن در مدرسهی شبانهروزی هم دانشآموزی کثیف و نامرتب بود و همیشه روی انگشتانش جوهری بود. او با بقیه هماهنگ نبود و بدتر از همه این که نمیخواست هماهنگ شود. آلن، خجالتی و منزوی بود و لکنت زبانش هم وضع را سختتر کرده بود. در حالی که جان تورینگ آیندهی درخشانی را نوید میداد. او برای خواندن و نوشتن دچار مشکل بود اما تصمیم گرفت تا خواندن را یاد بگیرد و در مدت سه هفته خواندن را یاد گرفت. جان تورینگ در سن یازده سالگی به شیمی آلی علاقه نشان داد، اما به موضوعات دیگر علاقهای نداشت و نمیتوانست به مدت طولانی به آنها توجه نماید.
وقتی خانم و آقای تورینگ از هند برگشتند، تصمیم گرفتند تا در دینارد بریتانی مسکن بگیرند تا از پرداخت مالیات معاف باشند. آنان از خانوادهی متوسطی بودند و نمیتوانستند فرزندان خود را به مدارس سطح بالا بفرستند چون استطاعات پرداخت شهریهی این مدارس را نداشتند. پس برای اجتناب از سرزنش دیگران باید به جاهای دوردست میرفتند بنابراین بچهها را به خانهی دیگری بردند.
آلن از تعطیلات در فرانسه لذت میبرد و به سرعت زبان فرانسوی را یاد گرفت. تحصیلات ممتاز سرانجام استعداد نهفتهی او را بیدار کرد، استعدادی که به ارث برده بود. جدّ پدری او ریاضیدان و از دانشمندان کمبریج بود و نیاکان انگلیسی ایرلندی مادر او در سال 1891 میلادی، کلمهی «الکترون» را اختراع کرده بودند. این حقیقت که او را به عضویت انجمن سلطنتی پذیرفته بودند، خانوادهای او را تحت تأثیر قرار میداد و لغزشهای احتمالی کسی را که میخواست دانشمند باشد، رفع و رجوع میکرد.
آلن جوان خیلی خوب نقشش را در جار و جنجالهای گروه شیمی مدرسه بازی میکرد، اما این فقط سرگرمی بود. اگر او میخواست از تحصیلات خوبی برخوردار گردد و وارد زندگی شود، باید زبان لاتین را میآموخت. این چیزی بود که برایش تحصیل کرده بود، این چیزی بود که همهی پولها برای آن خرج میشد. بنابراین باید چیزی یاد بگیرد، نه این که در کارهای گروه شیمی مداخله کند آلن بدون آموختن زبان لاتین هرگز از عهدهی امتحان ورودی مدرسهی عمومی بر نمیآید.
آلن تصمیم گرفت به شربورن که مدرسهای عمومی و نسبتاً آبرومند در دورست بود، وارد شود. آلن در سن سیزده سالگی به تنهایی از فرانسه حرکت کرد تا نخستین ترم تحصیلیاش را در مدرسهی جدید شروع کند. وقتی قایق او وارد سوس هامپتون شد، همان روز اعتصاب عمومی شروع شده بود. کشور در اعتصاب بود، هیچ نوع وسیلهی حمل و نقلی وجود نداشت. او نقشهای خرید و مسافت 55 مایلی تا شربورن را دوچرخهسواری کرد و قهرمان وارد شد.
اما تورینگ نتوانست مطابق قول و قرارش زندگی کند. خیلی زود روشن شد که او از قهرمانان مدرسه نیست. پسر کثیف و زشت با لکنت زبان، علاقهای به گرفتن دوست نداشت. او حتی علاقهای نداشت که برای خودش شهرتی کسب کند. او رفتاری غیر اجتماعی داشت و ترجیح میداد تا جایی که ممکن است درون هر سیستمی راه خودش را برود. این وضعیتی بود که تورینگ در سراسر زندگیاش دنبال میکرد. او خودش را با این وضعیت وفق داده بود.
تورینگ ورزش انفرادی دو استقامت را در مدرسه انتخاب کرد. شگفت این که تورینگ علی رغم داشتن پای صاف در این ورزش خوش درخشید. او از جهت جسمی هم مانند وضعیت ذهنی، اگر علاقه داشت همیشه استقامتی استثنایی از خود نشان میداد. او در شربورن توانست علاقهی عمیق خود را به ریاضیات کشف کند. او به درسهای خشک و کسل کننده علاقهی کمی داشت و به همین دلیل مطالعهی موضوعات مورد علاقهی خودش را دنبال کرد. آلن مطالعهی نسبیت را شروع کرد. او علاقهی وافری به رمزنویسی داشت اما نمیتوانست سوراخها را در ورقهی کاغذ درست کند. وقتی سوراخهای خاصی روی کاغذ خاصی ایجاد شود، پیامی در برخواهد داشت. اما برای به وجود آوردن پیامهای رمزدار به کسی نیاز بود تا آن را دریافت کند. تورینگ در سن 15 سالگی، این شخص را پیدا کرد. نام او کریستوفر مورکوم بود، او بهترین ریاضیدان مدرسه به حساب میآمد. علاقهی مشترک آنها به ریاضیات به زودی دوستی آنها را استحکام بخشید.
کریستوفر گاهگاهی از مدرسه غایب میشد و وقتی برمیگشت، بیحال و ضعیف به نظر میرسید. تورینگ میدانست که حال او خوب نیست، اما اطلاعی از وخامت اوضاع او نداشت. کریستوفر دچار بیماری سل گاوی بود. در اوایل سال 1931 میلادی به طور غیر منتظرهای در مدرسه حالش بد شد، او را به بیمارستانی در لندن بردند و چند روز بعد مرد.
تورینگ از کینگ کالج کمبریج در رشتهی ریاضی بورس تحصیلی گرفت. او در ماه اکتبر سال 1931 میلادی در سطح لیسانس فارغالتحصیل شد.
دانشگاه کمبریج در اوایل دههی 1930 میلادی، یکی از مؤسسات علمی و ریاضی پیشرو در جهان بود. سویسی فیزیکدان نظری انگلیسی، پاول دیراک و هم کلاسیهایش بعد از دانشگاه گوتینگن این دانشگاه را دومین مرکز مطالعهی فیزیک کوانتوم کرده بودند. کینگ کالج هم به آنها کمک کرد. جرج هاردی، یکی از بهترین ریاضیدانان زمان خودش و آرتور ادینگتن که کارهای او تئوری نسبیت اینشتین را تأیید کرد، هر دو در آن جا اقامت داشتند و تورینگ را آموزش دادند.
اما علاقهی جدی تورینگ به منطق ریاضی بود. راسل و وایتهد در سال 1913 میلادی در کمبریج کتاب «مبادی ریاضیات» را منتشر کرده بودند. این کتاب به یافتن مبنایی فلسفی برای ریاضیات کمک کرد. راسل و وایتهد کوشیدند تا نشان دهند که ساختمان کامل ریاضیات را میتوان از اصول موضوعهی منطقی اساسی و خاصی اقتباس کرد. (به نوعی؛ این برخلاف تلاش بول بود که نیم قرن پیش از آن انجام داده بود.) راسل و وایتهد به موفقیت کامل نرسیدند چون تلاش آنان بر معماهای منطقی خاصی مبتنی بود.
به این معمای منطقی توجه کنید: چیزی که من میگویم نادرست است. اگر این فرض درست است، پس چیزی که میگویم نادرست است و اگر این نادرست است، پس درست آن چیست. به زبان منطقیون، این قضیه نوعاً بینتیجه است. تا زمانی که چنین تناقضهایی حل نشده است، نمیتوان ریاضیات را بر اصول منطق بنا کرد. اما چنین قضایایی تلاش برای بنا کردن ریاضیات بر پایهی منطق صحیح را بیاعتبار نمیکند.
در سال 1931، وقتی که مجلهی اتریشی «کودک عصیانگر» دربارهی منطق متعلق به کورت گودل، مقالهاش دربارهی قضایای نوعاً بینتیجه در «مبانی ریاضیات» را منتشر کرد، همه چیز تغییر کرد. او در این مقاله فرضیهای را ارائه میکند که سبب نگرانی سایرین میشود که گویا آن را پایان دانش ریاضیات نام مینهد.
قضیهی گودل عبارت است از: این گزاره غیر قابل اثبات است و نشان داد که نمیتوان آن را اثبات کرد (یا این که به تناقض منجر میشود) و هم چنین نمیتوان نادرست بودن آن را اثبات کرد. گودال نشان میدهد که در سیستم هر دستگاه ریاضی، منطقی سختگیرانهای که بر اساس اصول متعارفی بنا شده است، همیشه قضایایی وجود دارد که یا غیر قابل اثبات است یا نمیتوان آنها را اثبات کرد. ریاضیات کامل نیست! بدتر از آن، به نظر میرسد که این نقص غیرقابل جبران است. به همین دلیل یقین نداریم که اصول متعارف اساسی حساب به تناقض منجر نمیشود. ریاضیات غیرمنطقی است! (و ترسناکترین چیز هم این است که منطق هم به این صورت باشد!)
این پیشرفتها تأثیر شدیدی روی تورینگ داشت. زیرا طبق معمول او در نخستین بخش از امتحانات ریاضی فقط افتخارات درجه دوم کسب کرد. اما در امتحان نهایی سطح خود را ارتقا داد و به همین دلیل او میتوانست در کمبریج بماند و به تحقیق بپردازد . ادینگتن و هاردی دربارهی تواناییهای استثنایی او تردیدی نداشتند.
تورینگ به عضویت کینگ کالج پذیرفته شد و به یکی از مغزهای ریاضی آیندهدار بریتانیا تبدیل شد.
رابطهی تورینگ با مادرش صمیمانه بود. او در نامههایی که به خانه مینوشت، دربارهی تفکرات ریاضیاش به مادر اطلاعاتی میداد، او دربارهی چیزهایی مانند نظریهی کوانتوم و نسبیت مینوشت. این که مادر تورینگ چه مقدار از این مطالب را متوجه میشود، جای سؤال است. او زنی باهوش بود، اما مذهبی بودن و عقیده به حفظ ظاهر در جامعه بیش از هر چیز دیگر در نظرش اهمیت داشت. او هنوز هم به آلن احترام میگذاشت، همانطور که از بچگی این طور بود. این نمونهای بارز بود که او کاری دون شأن خود را انتخاب کند تا در دلش ریاضیات به برتری برسد.
به هر حال تورینگ در ریاضیات از دیگران پیشی گرفت. اینک بهترین زمان بود که آخرین یپشرفتها را از برجستهترین ریاضیدانان و دانشمندان زمان خودش جذب کند. پس از آن که هیتلر در سال 1933 میلادی بر آلمان مسلط شد، بسیاری از بزرگترین تبعیدیهای آلمان به کمبریج رفتند و در آن جا تدریس کردند. این گونه بود که تورینگ سخنرانی شرودینگر را دربارهی مکانیک کوانتوم شنید، موضوعی که او تقریباً آن را اختراع کرد. تورینگ شنید که ماکس برن، استاد جوان دانشگاه گوتینگن در موضوع مکانیک کوانتوم تدریس جامعی دارد. استاد تبعیدی دیگر دانشگاه گوتینگن، ریچارد کورانت بود که معادلات دیفرانسیل درس میداد. برن و کورانت با دیوید هیلبرت، استاد ریاضیات در گوتینگن کار کرده بودند. دیوید هیلبرت را یکی از بزرگترین ریاضیدانان همهی اعصار معرفی کردهاند. او هم مانند راسل و وایتهد تلاش زیادی کرد تا ریاضیات را بر پایهای اسلوبدار بیان کند. و آن را از چند اصل متعارف بسازد تا بدین ترتیب همهی اشکال ریاضیات به وسیلهی قواعد روشن از آن پیروی کنند.
برنامهی هیلبرت، چنان که معروف است با نظریهی هیجانانگیز و مشهور گودل به توقفی تکان دهنده انجامید. گودل اثبات کرد که ریاضیات از نظر منطقی فاقد ثبات است. نظریهی گودل علی رغم قصد اولیهاش موفق نشد تا ریاضیات را نابود کند. مردم و به خصوص ریاضیدانها صرف نظر از این حرفها به استفاده از ریاضیات ادامه دادند. مثلث همیشه مثلث است، پلها فرو نریختند و بودجهی ملی هنوز به نظر میرسد که افزایش مییابد، اما این نقص دانش ریاضیات نبود. در حقیقت خیلیها به سادگی به اثبات گودل به صورت استنباطی نامربوط به نگاه میکردند. در ریاضیات حقیقت موضوعیت دارد، نه رابطهی منطقی. اما آیا حقیقت و عدم وجود رابطهی منطقی با یکدیگر هماهنگ هستند؟
صرف نظر از چنین جر و بحثهایی، در نظریهی گودل هنوز سؤالات ریاضی خاصی حل نشده باقی ماندهاند. اینها راه کاهش صدمات را نشان میدهند. با توافق انجام شده، سیستم متعارف از قبیل دانش ریاضیات میتواند قضایای اختیاری بیافریند، چه این قضایا قابل اثبات باشندیا نباشند. اما آیا مشخص کردن این که چنین قضایایی درون سیستم هم اختیاری میباشد، امکانپذیر است؟ به عبارت دیگر، آیا چنین قضایای اختیاری را با به کار بردن مجموعهای از قواعدی که از اصل موضوع ناشی میشود و سیستم بر آن مبتنی است، میتوان شناسایی کرد؟ آیا با مجموعهای از مراحل مشخص یعنی دستورات مکانیکی که هر کس بتواند دنبال کند، میتوان آن را معلوم کرد؟ اگر چنین است، قضایای اختیاری را به سادگی میتوان معلوم کرد و کنار گذاشت. آنها را نتوان مشخص کرد، همه چیز گم میشود. به عبارت دیگر ریاضیات با عدم هماهنگی محلی به استهزا گرفته میشود.
این مسئلهای بود که تورینگ در آن زمان سعی میکرد پاسخ مناسبی برای آن بیابد. این مسئولیتی بلندپروازانه بود، برای هر سؤال یک راه حل در ریاضیات اساسی وجود داشت. تورینگ برای از میان برداشتن این مشکل، مفهومی را اختراع کرد که باید پیامدهایی در ورای ریاضیات داشته باشد.
کدام روشهای (قواعد) مکانیکی برای مشخص کردن این که آیا قضیهای ریاضی قابل اثبات است یا نه، مورد استفاده قرار میگیرند؟ چنین قواعدی دقیقاً به اصل حساب مربوط میشود. عدد قابل محاسبه چیست و چطور باید آن را محاسبه کرد؟ محاسبه، فرایندی سخت است لذا میتوان با ماشین آن را ادامه داد. تورینگ برای پی بردن به ماهیت نظری چنین ماشینی تلاشیهایی را شروع کرد که امروز به ماشین تورینگ شناخته میشود.
این ماشین فقط بر اساس قواعد کار میکرد و میتوانست هر چیزی را که برای آن الگوریتم وجود داشت محاسبه کند، یعنی ترتیب دقیقی از مراحل که به محاسبه میانجامد.
برای نمونه، فرایند کشف فاکتورهای عدد را در نظر بگیرید (یعنی، اعداد اول که با آن قابل تقسیم باشد). مثال ساده: برای کشف فاکتورهای عدد 180 آن را به کمترین عدد اول بخشپذیر تقسیم کنید تا دیگر قابل تقسیم نباشد، سپس این فرایند را با عدد اول تصاعدی بعدی تکرار کنید تا تقسیم کامل شود. (اعداد اول به اعدادی میگویند که فقط بر خودشان قابل تقسیم باشند. مانند 13،11،9،7،5،3،2...)
2=90÷180
2=45÷90
3=15÷45
3=5÷15
5=1÷5
*
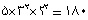 بنابراین:
بنابراین:این فرایند یا الگوریتم به صورت خط ایرانیک نوشته شده است و میتوان آن را برای هر عددی به کار برد. میتوان آن را از نظر مکانیکی هم به کار برد، یعنی با ذهن مکانیکی یا ماشین ذهنی هم قابل استفاده است.
چنین ماشینی را برای اجرای کارهای خاص میتوان ساخت تا بر اساس برنامه، کار خاصی را انجام دهد.اگر این قواعد برای محاسبهی اعداد اول در نظر گرفته شوند، اعداد اول را محاسبه میکند. اگر قواعد شطرنج را به آن بدهیم، ماشین میتواند شطرنج بازی کند. هر ماشینی به سادگی برنامهای را که به آن میدهیم، دنبال میکند.
تورینگ چیزی را فرض گرفت و آن را ماشین جهانی نامید. با این ماشین میتوانستند عددی بدهید که برنامهی سایر ماشینهای تورینگ را رمزگذاری کند. سپس ماشین این برنامه را دنبال میکرد و به روش غیرقابل تشخیصی در برابر ماشین اصلی تورینگ عمل میکرد، مثلاً شطرنج بازی میکرد، یا اعداد اول را محاسبه میکرد.
از این نقطه نظر (تئوری خالص)، تورینگ دفاع از تز خود را شروع کرد. چیزی که گودال ابراز میداشت منطقی بود. چیزی که تورینگ در آن زمان استدلال کرد، به تئوری گودل شباهت داشت (در استدلالها)، اما مورد او ریاضیات بود.
تورینگ نوعی ماشین را پیشنهاد کرد که در سیستم ریاضی قضایای اختیاری را میشناخت. این ماشین نظری همان ماشین جهانی تورینگ بود. این ماشین را با عددی تغذیه میکرد که ماشین دیگر تورینگ آن را رمزگذاری کرده بود و سپس به همان روش عمل میکرد. اما اگر این ماشین فرضی جهانی با عدد دیگری که وصف خودش بود رمزگذاری میشد، به چه صورت عمل میکرد. چطور این ماشین مانند خودش رفتار میکرد، رفتارهای خاص خودش را داشت و مانند خودش عمل میکرد... و چطور ماشین میتوانست این برنامه را مانند خودش دنبال کند، وقتی که قبلاً مانند خودش دنبال کرده است؟
واضح است که ماشین دیوانه میشود. به زبان تئوری، ماشین با تناقض رو به رو میشود. چنین ماشینی حتی به صورت تئوری هم نمیتواند وجود داشته باشد. معنی این حرف این است که چنین محاسبهای را واقعاً نمیتوان انجام داد. به کار گرفتن مجموعهای از قواعد در صورتی که فرضی قابل اثبات (یا عدم اثبات) و عملی باشد و فقط از برنامهی درون آن سیستم استفاده کند، امکانپذیر نیست.
نه تنها ریاضیات از نظر منطق ناکامل است، آن طور که گودل نشان داده بود، از نظر ریاضی هم ناقص است. در ریاضیات روشی وجود ندارد که بتواند خودش را از قضایای اختیاری جدا کند. تورینگ کشفیات خود را در مقالهای به نام «دربارهی اعداد قابل محاسبه با کاربرد برای مشکل تصمیمگیری» منتشر کرد. کلمهی نامأنوس بعدی به شکل تصمیمپذیری اشاره دارد که هیلبرت آن را پیشنهاد کرد.
همهی کسانی که به طور مبهمی آن را شناختند، متوجه شدند که مقالهی تورینگ جنجالی بود. گرچه در آن دورهی پیش از کامپیوتر کسانی که آن مقاله را بفهمند کم بودند ولی آنها پی بردند که این مقاله تاریخساز است. سابق بر آن، مفاهیم محاسبهپذیری اصلی ریاضی و اعداد قابل محاسبه نامشخص بودند. ولی آنها روشن شدند. محاسبه به زبان دقیق ریاضی تعریف شد، یعنی به قدری دقیق بود که طرح نظری را برای ماشینی که بتواند آن کار را انجام دهد، شروع کردند. در عین حال، تورینگ محدودهی کارهایی را که این ماشین میتواند انجام دهد مشخص کرد.
ماشین تورینگ کامپیوتر نظری بود. امروزه آن را نخستین نمونهی کامپیوتر دیجیتال الکترونی میشناسند. تورینگ نقشهی تئوری کامپیوترها را پیش از آن که کامپیوتر حتی ساخته شده باشد، رسم کرده بود.
اما در سال 1937 میلادی، وقتی که سرانجام مقالهی تورینگ منتشر شد، هنوز خارج از ظرفیت فهم جامعه بود. (برای انتشار آن مقاله مدتی درنگ شد زیرا هیچ کس واجد شرایطی وجود نداشت تا دربارهی خلاقیت و نوآوری مقاله تورینگ داوری کند). زمانی که مقالهی اعداد محاسبهپذیر منتشر شد، تورینگ از اقیانوس اطلس عبور کرد و مدرک دکتری خود را در پرینستون دریافت کرد. در آن جا ساختمان بخش ریاضی مرکز مؤسسهی تازه بنیان برای مطالعات پیشرفته تأسیس شده بود. این مرکز برای تحقیق علمی نظری در سال 1933 میلادی تأسیس شده بود و به سرعت به بهترین مرکز در نوع خودش در جهان تبدیل شد. اما در این دوره مانند چند تن از اعضای ارشد آلمانی و یهودیاش کاشانهی ثابتی نداشت. تورینگ آن زمان خود را بین الههها دید. اینشتین و گودل هم مانند کورانت و هاردی در استراحت بودند. اکثر آنان عزلت گزین شده بودند و خیلی کم از مرد جوان انگلیسی اطلاع داشتند.
تورینگ با یکی از قهرمانان المپیک تماس گرفت، او ریاضیدانی اتریشی مجارستانی به نام فون نیومن بود. او انسانی فرهیخته بود و برای فرمولی حیرتآور در هر زمینهای چه ریاضیات یا آشپزی به طور یکسان کلاهش را به نشانهی ابراز احساسات برمیداشت. فون نیومن بود که به موفقیت بزرگ تورینگ پی برد. او فهمید که جوان انگلیسی در حقیقت موضوع جدیدی را خلق کرده است. (تورینگ آن را قابلیت محاسبه نامید، به عبارت دیگر: این موضوع به قدری جدید بود که هنوز اسم نداشت.) فون نیومن بود که به احتمال عملی شدن این موضوع پی برد. او دانست که گام بعدی ساختن ماشین تورینگ بود.
در ضمن، تورینگ برای گرفتن پی اچ دی ادامه داد که به مشکلات دیگر هیلبرت ارتباط پیدا میکرد. هیلبرت در سال 1900 میلادی، 23 مسئلهی مهم را برای ریاضیدانان قرن بیستم عنوان کرد تا آنان حل کنند. باید در تغییر قرن این خوش بینی هیلبرت را افزود که همهی مسائل ریاضی قابل حل هستند. تورینگ قبلاً آن را غلط اثبات کرده بود، اما سرانجام تصمیم گرفت تا برای حل مشکل مربوط به فرضیهی ریمن تلاشی پیگیر نماید. هیلبرت آن را مهمترین مسئله در ریاضیات مینامید. هاردی قبلاً با این مشکل به مدت 30 سال به طور متناوب اما بیهوده دسته و پنجه نرم کرده بود.
به زبان ساده، مسئلهی منتسب به تورینگ به تعداد اعداد اول مربوط میشد. در اوایل دههی 1790 میلادی کودک نابغهی پانزده سالهی آلمانی به نام کارل گاوس را دیدند که با چند نفر از به اصطلاح ریاضیدانها با نیوتن رقابت میکردند. او کشف کرده بود که اعداد اول بر طبق الگویی منظم فراوانی کمتری دارند. در مورد عدد n فضای بین اعداد با لگاریتم طبیعی n افزایش مییابد. چنین چیزی به اشتباهات حاشیهای منجر میشد. برنارد ریمن، بعد از گاوس استاد ریاضیات در دانشگاه گوتینگن شد و سبب پیشرفتهایی در این موضوع شد که مستلزم پیچیدگی زیاد فرضیهی ریمن بود.
کشف شده است که روش لگاریتم برای اعداد اول کمی مبالغهآمیز است و پس از میلیونها محاسبه حتی با اعداد بزرگتر، آنها را هم تأیید میکرد. فرض شده بود که این موضوع همیشه به همین صورت است. سپس یکی از همکاران هاردی به نام ج. ا. لیتلوود، کشف کرد که اگر فرضیهی ریمن درست بود، موضوع به این صورت نبود. یک تغییر یا برآورد کمتر از حد در برخی جاها قبل از عدد ده به توان ده به توان ده به توان 34 اتفاق میافتد.
این عدد به شکلی باور نکردنی بزرگ است. چنان که هاردی اشاره کرده است: این عدد بزرگترین عددی است که تا آن زمان برای منظورهای خاص در ریاضیات به کار رفته است. بنا به ادعای هاجز، نویسندهی زندگینامهی تورینگ، حتی عدد ده به توان ده به توان 34 که به صورت عدد صحیح نوشته میشود، کتابهای بزرگتر از سیارهی مشتری را پر میکند.
مسائلی که در این جا مطرح شد برای نظریهی اعداد اصولیاند. (فرضیهی ریمن، برای نمونه تا به امروز اثبات نشده است.)
تورینگ، آمریکا را سرزمینی خوشایند و شوق برانگیز یافت. او زیاد کار میکرد و وقت زیادی را صرف خودش میکرد.
تورینگ بعد از دو سال اقامت در آمریکا به بریتانیا برگشت و پیشنهاد فون نیومن برای همکاری با او در مؤسسهی مطالعات پیشرفته را نپذیرفت. عضویت جدید تورینگ در کینگ کالج تجدید شد و او به زندگی عادی خود در کمبریج برگشت. او نامهای دربارهی خرس اسباببازی خانهشان به مادرش نوشت و از او خواست تا فیلم سفید برفی و هفت کوتوله را در سینمای محلی ببیند. تورینگ به طور خاص تحت تأثیر صحنهای بود که جادوگر شریر سیبی را از روی ریسمان پایین میآورد و وارد زهر جوشان میکند و این ورد را میخواند.
سیب را درون زهر فرو کن *** تا مرگ در حال خواب آن را بخورد
کسانی که شنیدند او آواز میخواند، باور نمیکردند که اخیراً با خوردن سیبی خودکشی کرده بود.
در همان ایام بود که تورینگ با فیلسوف اتریشی لودویگ ویتگنشتاین ملاقات کرد و در کلاس درس او شرکت کرد. ویتگنشتاین برای افراد خاصی تدریس میکرد. او به کسانی درس میداد که انتظار داشت روی صندلی راحتی اتاق خالی او بنشینند و وقتی که افکار خود را آشکار میکرد به او گوش فرا دهند. آنها باید مدتی طولانی با سکوتی عذابآور بنشینند و بعد سؤالی بپرسند. به دنبال این سؤال، اگر کسی جسارت داشت تا به آن جواب دهد مورد مؤاخذهی جدی قرار میگرفت.
ویتگنشتاین بر مبنای ریاضیات اما از نقطه نظر فلسفی درس میداد. او میخواست ماهیت دقیق ریاضیات را حتی در دقیقترین حالت و صرف نظر از کاربردهایی که دارد کشف کند. تورینگ نیروی فکری و فلسفی ویتگنشتاین را نداشت. هیچ انسان دیگری روی زمین چنین نیروی ترسناکی را نداشت. او ریاضیدانی برتر بود. اما تورینگ از حملهی نگاههای ترسناک ویتگنشتاین مرغوب نمیشد.
ویتگنشتاین از یک نقطه نظر معتقد بود که سیستمهایی مانند ریاضیات یا منطق علیرغم تناقضاتی که در آنها وجود دارد، هنوز هم معتبر هستند. تورینگ اثبات کرده بود که ریاضیات تنافراتی را شامل میشود اما آنها کاملاً مانند تناقضات نیستند. او برای ویتگنشتاین توضیح داد که اگر پلی را بر مبنای ریاضیات بسازید به طوری که در آن تناقض وجود داشته باشد، آن پل فرو میریزد. از طرف دیگر ویتگنشتاین تأکید کرد که: ماهیت ریاضیات و کاربرد آن موضوعاتی مجزا هستند. اما تورینگ در مقالهی اعداد قابل محاسبه قبلاً نشان داده بود که چه ارتباط تنگاتنگی بین ریاضیات کاربردی و محض وجود دارد. او مسئلهای نظری و اساسی در ریاضیات را با پیشنهاد «ماشین» حل کرد. درحالی که آن مشکل نظری بود ولی میتوانستیم ماشین یا ابزاری واقعی را بسازیم.
تورینگ به نحو جالبی نشان داد که در هر سیستمی (مانند ریاضیات یا منطق) قضایای تصمیم ناپذیر وجود دارد که فلسفهی اخیر ویتگنشتاین را رد میکند. ویتگنشتاین مدعی بود که هر مشکلی، مادامی که به زبان منطقی صحیح بیان شود، قابل حل است.
تورینگ در آن زمان با قدرت وارد قلمرو ریاضیات کاربردی شد در سال 1939 میلادی جنگ علیه آلمان نازی شروع شد و تورینگ برای اهداف اطلاعاتی مأمور خدمت شد. او را با تیمی از اینتلیجنت سرویس برای کشف رمز بلتچلی پارک در 60 مایلی شمال لندن فرستادند. این پروژهای فوق سری بود که تحت شدیدترین کنترلهای نظامی بود. تلاشهای تورینگ و تیم رو به فزونی اطلاعاتی در بلتچلی تقریباً مسیر جنگ را عوض کرد.
داستان بلتچلی در سال 1938 میلادی شروع شد، وقتی مهندس جوان لهستانی به نام رابرت لوینسکی سفارت بریتانیا در ورشو را کشف کرد. او ادعا کرد که در کارخانهای در آلمان کار کرده بود که در آن جا ماشینهای تولید رمز میساختند. لوینسکی جزئیات ماشین را به خاطر سپرده بود. او خیلی زود و به شکل قاچاقی از لهستان به پاریس رفت و در آن جا تولید ماشین را سرپرستی کرد. بریتانیا دربارهی این ماشینها اطلاعاتی کسب کرده بود. آن ماشینها معما نامیده میشدند و فرماندهان ارتش آلمان برای فرستادن دستورات رمزی به نیروهایشان در جبههی جنگ از آنها استفاده میکردند. فرماندهان زیر دریاییهای آلمان برای شناسایی موقعیت خود از آنها استفاده میکردند، بنابراین میتوانستند آنها را به سوی نزدیکترین کاروان دریایی دشمن بفرستند.
کشف این رمزها به طور شگفتآوری ساده بود، در حالی که سیستم رمزگذاری کامل و ظاهراً شکست ناپذیر بود. اساساً این سیستم شامل دو ماشین است. ماشین فرستنده با کلیدی شروع به کار میکردم و پیام بدون رمز به سادگی در آن نوشته میشد. این پیام از طریق بازوهای چرخانهی الکتریکی به طور خودکار بر طبق این کلید به صورت رمز درآمده و سپس پیام را میفرستادند. در طرف دیگر، ماشین دریافت کنندهی رمز به همان صورت شروع به کار میکرد و این پیام رمزگشایی شده و به صورت بدون رمز نوشته میشد. چرخانهها به طور خودکار امکان میداد تا میلیاردها کلمهی دگرگون شده به وجود بیاید، به طوری که هر دشمنی که رمز ارسالی را به دست میآورد اگر میخواست رمز را باز کند با کار واقعاً غیرممکنی رو به رو بود. هزاران پیام هر 24 ساعت ارسال میشد و کلید آن هر روز تغییر میکرد. آلمانها مطمئن بودند که سیستم ارتباطی آنها غیر قابل نفوذ است.
اپراتورهای اطلاعاتی بریتانیا در بلتچلی فهمیدند که ماشین رمز دقیقاً چطور ساخته شده و کار میکند اما این کافی نبود. پیچیدگیهای ماشین رمز بسیار زیاد بود. هر زمان که نامهای نوشته میشد، وقتی آن را به صورت پیام مینوشتند، چرخانهها یک بار بیشتر میچرخیدند. بنابراین حتی اگر همان نامه چند بار چاپ شود، تقریباً همیشه نامههای مختلفی به شکل رمزدار دریافت میشد. برای کشف رمز باید کلیدی را که ماشین بر اساس آن تنظیم شده است بشناسیم، چون به تنهایی موقعیت اولیهی چرخانهها را آماده میکند. وقتی که دقیقاً سه چرخانه استفاده میشود، یکی از میلیونها (
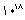 ) به توان 18 احتمالات مربع است. پیامهای فوق سری را با ده بازوی چرخانه به ماشین رمز میفرستادند.
) به توان 18 احتمالات مربع است. پیامهای فوق سری را با ده بازوی چرخانه به ماشین رمز میفرستادند.تورینگ و گروه او (که آن موقع بهترین مغزهای ریاضی کشور را شامل میشد) با کاری عظیم رو به رو بودند. آنها باید هزاران پیام رمزدار را جستو جو کنند، هیچ ترکیبی را نادیده نگیرند و احتمالاتی را که تا اندازهای معنی چیزی را داشته باشند، بررسی کنند و بدین ترتیب خیانتی که در تنظیمات خاص وجود دارد را جستوجو کنند. تورینگ بلافاصله موقعیت را با مهارت خاصی ارزیابی کرد. در این تئوری، مشکل کاملاً ساده بود. جوابی برای ماشین تورینگ بود. ماشینی که تورینگ در مقالهی اعداد قابل محاسبه توصیف کرده بود، تئوری محض نبود. تورینگ ماشینی را پیشبینی کرده بود که دستورات را با نوار کاغذی به آن میدادند. نوار هم به مربعهایی تقسیم میشد که ماشین هر بار یکی از آنها را میخواند. در سادهترین شکل، هر مشکلی را میتوان به مجموعهای از دستورات با ارقام دوتایی (بیت) خلاصه کرد. تورینگ به درستی گمان میکرد: مسئلهای که با رمز نشان داده شود، مسئلهای قابل حل است. یعنی اگر دستورات درستی به ماشین تورینگ داده شود، میتواند جواب بدهد. در مورد این تئوری، روی هم رفته کار عملی موضوع دیگری است.
تورینگ و گروه او ساخت ماشین الکترومغناطیس دیگری را شروع کردند که میتوانست با سرعت زیادی با پیام رمزدار تنظیم شود، نظاماتی را جستوجو کند و ویژگیها یا ترکیباتی را دوباره تکرار کند که ممکن است برای رمزگشایی قابل بررسی باشد. (برخی اوقات، در نتیجه عمل دشمن، آنها میتوانستند این کلید را برای برخی پیامهای قبلی به کار گیرند. در نتیجه دید بهتری میداد که رمز چگونه کار میکند، اما فقط کلیدی قدیمی تولید میکرد). ماشین رمزگشایی تورینگ به مجسمهای عظیم معروف شد و چنین دشواریهایی سبب شد تا ده نسخه از این ماشین در بلتچلی ساخته شود. نخستین ماشین عظیمالجثه در ماه دسامبر سال 1943 میلادی شروع به کار کرد. جزئیات چنین ماشینی توسط حکومت و ارتش بریتانیا مخفی مانده بود. (تا زمان اخیر برخی رمزها که در جنگهای ناپلئون به کار میرفت، جزء اطلاعات طبقهبندی شده قرار میگرفت.) به نظر میرسد ماشین کلوسس از 2400 لولهی توخالی که به صورت دوتایی محاسبه میکرد، استفاده مینمود. اینها در حالی که مثل کامپیوتر وظایفی را انجام میدادند اما برنامهی ذخیره شده را شامل نمیشدند. بنابراین، آیا ماشین تورینگ واقعاً ماشین تورینگ بود؟ این مطالب هنوز مورد بحث قرار میگیرند. به هر حال، کلوسس در سطح وسیعی به صورت پیشتاز کامپیوتر دیجیتال الکترومغناطیس مورد توجه قرار گرفت.
کلوسس جهش بزرگی در فنآوری بود. نیروی مرکب پنج دستگاه عملآوری آن میتوانست تا 25000 علامت را در ثانیه اسکن کند. اما حتی این هم کافی نبود. زیر دریاییهای آلمان نازی در آن زمان کاروان کشتیهای متحدین در اقیانوس اطلس را غرق میکردند. اما انجام هیچ کاری میسر نبود هنوز مدتی لازم بود تا رمز پیامهای ارسالی و دریافتی از زیر دریایی آلمانها رمزگشایی شود. آنها روز و شب کار میکردند. کلوسس مدت رمزگشایی را به چند ساعت و بعد به چند دقیقه تقلیل داد. سرانجام موقعیت زیردریاییهای آلمانی در اقیانوس اطلس معین شد و فقدان کشتیها در ارتش متحدین به نحو چشمگیری کاهش یافت.
آلمانها شک کردند اما هم چنان عقیده داشتند که رمز سری غیرقابل دسترسی است. انگلیسها به آسانی اطلاعات را از شبکهای از جاسوسها دریافت میکردند. تورینگ ماشین رمزگذاری را اختراع کرد اما دیگر نیازی به اختراع ماشین رمزگذاری پیشرفته نبود.
تورینگ علیرغم ظاهر شلخته و نامرتب و ساعات کار نفسگیر، همان مرد سرحال استثنایی همیشگی بود. هفتهای چند بار از محل کار خارج میشد و در جنگل و دشتهای اطراف میدوید. مردم محلی شگفتزده مشاهده میکردند که او در حال دویدن مشتی علف در دست دارد و آن را میجود. تورینگ با این روش کمبود ویتامین برنامهی غذایی زمان جنگ را جبران میکرد. (سابق بر این، همیشه پیش از آن که برای خوابیدن به بستر برود، سیب میخورد).
تورینگ با شروع جنگ متقاعد شده بود که به بریتانیا اعزام خواهد شد. او پساندازش را به صورت شمش نقره در آورده و مخفیانه در جنگل نزدیک پارک بلتچلی دفن کرده بود. سپس محل دفینهایش را رمزگذاری کرد و به حافظه سپرد. اما پس از آن که جنگ تمام شد، او نتوانست رمزها را به خاطر آورد. تورینگ هرگز برای پیداکردن شمشهای نقره تلاش نکرد، علیرغم این که برنامهی سیستماتیک و کاملی را برای کشف گنج طراحی کرد و حتی تا آن جا پیش رفت که فلزیاب خودش را اختراع کرد. کار رمزگشایی در بلتچلی از حد یافتن محل زیر دریاییهای آلمان نازی فراتر رفت. چندی بعد تمام ارتباطات آلمانها مانند کتابی گشوده بود. این کار چنان اهمیتی داشت که در یک مرحله تورینگ از اقیانوس اطلس عبور کرد تا رابط آمریکاییها باشد. در حین سفر به فون نیومن برخورد کرد که ایدهی مربوط به اعداد قابل محاسبه را به صورت عملی درآورده بود. در بخش مهندسی دانشگاه پنسیلوانیا، آمریکاییها کار روی دستگاه عددی الکترونیکی انتگرالگیر و حسابگر را شروع کرده بودند. این کلوسسی برتر از هر کلوسس دیگر بود، شگفت این که شامل 19000 لامپ خلاء بود اما این دستگاه تا بعد از جنگ به کار نیفتاد. در بیخبری متحدین، آلمانها هم روی این موضوع کار میکردند. در سال 1943 میلادی کونراد زوس نخستین ماشین حساب برنامهریزی شدهی چند منظوره را تولید کرد. از این دستگاه برای تجزیه و تحلیل تولید بمبهای پرنده استفاده میشد، اما آزمایشگاه زیرزمینی زوس در برلین یک سال بعد بمباران شد.
تورینگ تا پایان جنگ در پارک هانس لوپ کار میکرد که درست در پایین جادهی بلتچلی قرار داشت. تا آن زمان، کار تورینگ در کلوسس شناخت او را از ماشین الکترونیک تعمیق بخشیده بود. تورینگ دربارهی این مسئله اندیشید که چگونه میتوان ماشینهایی ساخت که از ذهن انسان تقلید کنند.
در سال 1945 میلادی، تورینگ به آزمایشگاه فیزیک ملی تازه تأسیس در تدینگتن خارج از لندن پیوست. او در آن جا سرپرستی پروژهی ساخت موتور حساب خودکار (ا. سی. ای) را به عهده گرفت. تورینگ طرح یکپارچهای برای کامپیوتر برنامهدار دیجیتالی و الکترونیکی را شروع کرد. تورینگ برای ساخت این دستگاه و کار با کلوسس به اندازهی زیادی از تجربیات خود استفاده کرد، اما نکتهی مهم آن به صورت تئوری باقی ماند. مانند ماشین جهانی تورینگ که به صورت اعداد قابل محاسبه فرض شده بود، دستگاه فوق هم باید با طرح منطقی و کلی هم خوانی داشته باشد و بسیاری از برنامههای منطقی پیچیده را اجرا کند. اما این دستگاه با دشواریهای فنی رو به رو شد که تورینگ علاقهای به آنها نداشت. طرح او راه آیندهاش بود، یعنی بسیار برتر از نخستین ماشینهای فوق نیومن بود که در آن زمان در آمریکا در شرف تکمیل بود و هم چنین خیلی پیشرفتهتر از پروژههای تحت مطالعه در انگلستان بود. اما دستگاه فوق با دشواریهای فنی زیادی رو به رو شد. ضمن این که کمبود بودجه و سیاست علمی هم مشکلات جدیدی را به آن اضافه میکردند.
برخلاف دیگر زمینههای فعالیتهای علمی، سیاست علمی با کمبود بودجه رونق مییابد. به دلیل کمبودهای بریتانیای بعد از جنگ سیاستهای علمی به پیشرفت تاریخی بزرگی دست یافت و وارد دورهی مخفی کاری خود شد. چنین پیچیدگیهای ظریفی خیلی فراتر از تفکر ریاضیدان صرفاً جادوگری از نوع تورینگ بود. تورینگ در بهترین شرایط هم سیاست باز نبود و به زودی دریافت که روشهای او برای کسب بودجه مورد بیاعتنایی قرار میگیرد.
در سال 1947 میلادی تورینگ از آزمایشگاه فیزیک ملی استعفا و آن جا را ترک کرد تا دیگران پروژهی فوق را تکمیل کنند. مشخص نیست که آیا خودش استعفا کرد یا مجبور به استعفا شد. از قضای روزگار، این بهترین چیزی بود که میتوانست برای تورینگ اتفاق بیافتد. او به کمبریج برگشت تا در آن جا بیدرنگ روی تئوری کامپیوتر کار کند. او علیرغم مشغلهای که در کلوسس داشت، مبانی موتور کامپیوتر خودکار را طراحی کرد (سرانجام ساخته شد و با موفقیت آزمایش شد). مشغلهی آیندهی او برای پیشرفت کامپیوتر بود. کار نظری تورینگ بود که نام او را به ذهن متبادر میکند.
دیدیم که تورینگ از همان ابتدای کار، ماشینی را در ذهن خود تجسم کرده بود که عهدهدار انجام وظایفی بود که ذهن بشر انجام میدهد. اما آیا ماشین میتواند کاری معادل ذهن انسان انجام دهد؟ تورینگ آن موقع مفهوم «ماشین هوشمند» را پیشنهاد و تجزیه و تحلیل کرد. بسیاری از اهداف، با تدبیری خاص، رنگ میبازند. اهداف علمی و فلسفی جدیتر میشوند. ماشین هوشمند مستلزم داشتن شیوهی مکانیکی است که به آن هوش میگویند و معنی دیگر آن جبر است. به نظر میرسد که هوشمندی انسان، عنصری از ارادهی آزاد را در خود دارد. بحثهای فلسفی خسته کننده و بیفایده بین ارادهی آزاد و جبرگرایی در این جا بیربط است. نقطه نظر تورینگ این بود که ذهن بشر به طرف بیرون شکوفا میشود، گویی دارای اراده است. ذهن انسان چنان رفتار میکند که میپنداری عمل میکند.
بنابراین کارکردهای هوش صرفاً مکانیکی نیست، بلکه آنها را با ماشین میتوان اجرا کرد. آیا نظر او غیر منطقی بود؟ شاید. اما تورینگ از جهت دیگر با تجربه بود، چون در زمان جنگ روی کلوسس و دلیله کار کرده بود. اینها هر دو ماشینهایی جبری بودند، در حالی که کشف شده بود آنها هم توانایی رفتار تصادفی را داشتند. بیدلیل نبود که کلوسسی به تیمی متشکل از دوازده مراقب نیاز داشت تا آن را در مسیر صحیح نگه دارد.
این ماشینهای کامپیوتری اولیه در یک سطح کاملاً جبری بودند. در حالی که در سطح دیگر، آنها رفتار تصادفی مجزایی را به نمایش میگذاشتند که به نظر میرسید تقلیدی از ارادهی آزاد بودند. نقطه ضعفی وجود داشت: یک مورد کوچک، اما واقعی.
نکتهی اصلی که تورینگ به آن پی برد این بود که ماشینها میتوانند بیاموزند. در این روش ماشینها میتوانند توانایی خود را به فراتر از کارهای مکانیکی گسترش دهند. میتوان ماشین را آموزش داد که کارش را بهتر انجام دهد تا جایی که «هوش» خود را به نمایش بگذارد. در این جا تورینگ بر مشکل بالقوهی دیگر غلبه کرد که ممکن بود تز او را محدود کند. ممکن است ماشین هوش خود را نشان دهد، اما ممکن است بازتابی از هوش پدیدآورندهی آن هم باشد.
تورینگ آن را قبول نداشت. او از مقایسهی معلم و شاگرد استفاده کرد. شاگرد میتواند بر معلمش پیشی بگیرد و هوش کیفی برتری را بسط دهد و با کمک معلمش از اطلاعات برنامهای که برایش تهیه شده استفاده کند.
تورینگ سپس به بحثهای بیشتری پرداخت. امکان داشت ماشینی ساخته شود که با قواعدی که به آن داده میشود شطرنج بازی کند اما بازی کردن علیه چنین ماشینی، احساس خاصی میدهد که شخص با عقل خود در برابر چیزی زنده روبه رو میشود. از آن جا که کامپیوتر هم میتواند بیاموزد، کار آن از جبر مکانیکی فراتر میرود و مؤلفهی آزادی را مانند هوس زنده به نمایش میگذارد (لزوماً انسان نیست).
تورینگ سؤالاتی میپرسید که از آغاز مباحث فلسفی مورد پرسش بودند. اینها برای انسان چه معنی میدهد؟ هوش انسان دقیقاً چیست؟ اما او از نقطه نظر تازهای به این سؤالات گرایش داشت. آیا برای ماشین امکان داشت تا این خصوصیات را بفهمد؟ چطور تشخیص میدهیم که پدیدهی هوشمند، انسان یا ماشین است؟
تورینگ در سطحی فکر میکرد که از ریاضیات، اعداد قابل محاسبه یا حتی کامپیوترها فراتر بود. در حقیقت او فکرش را در جریاناتی مشغول کرده بود که از جهان تلقی خاصی داشت، گویا او هم کامپیوتر بود. چنان که او دربارهی گسترهی اندیشه کاوش کرده بود، مکانیک کامپیوتر نصف فکر او بود. هوش چیست؟
این هماهنگ شدن با ماشین به زودی تمام زندگی او را در برگرفت. در مورد خودش، ماشین آرامش روحی فوقالعادهای را در برابر ناآرامی مداوم زندگی درنی برایش فراهم کرد.
مراجعت تورینگ به کمبریج بهترین اتفاقی بود که برای کار و زندگی او پیش آمد. کار و زندگی تورینگ تفکیکپذیر نبودند. تورینگ از نظر روانشناسی مانند کامپیوترش بود، اما رفتار او آن را نشان نمیداد.
تورینگ در آن زمان 35 ساله بود، گرچه قیافهی او ده سال جوانتر نشان میداد. او در کینگ کالج اتاق داشت. تورینگ یکی از بهترین مغزهای کمبریج بود.
در ضمن در آن زمان پیشرفتهای بزرگی در حوزهی عملی شکل گرفته بود. ماشین حسابگر، کامپیوتر خودکار و ذخیرهسازی الکترونیکی را میشناختند که در کمبریج ساخته شده بود، اما با شگفتی تمام تورینگ از تماس با تیم مسئول آن اجتناب کرد. به جای آن پس از یک سال در کمبریج، سمت قائم مقامی آزمایشگاه کامپیوتر را در دانشگاه منچستر به عهده گرفت. آنها در آن جا مشغول ساختن ماشین دیجیتال و اتوماتیک منچستر بودند.
ماشین فوق نخستین کامپیوتر برنامهریزی شدهی الکترونیکی آماده به کار بود. در روز بیست و یکم ژوئن سال 1948 میلادی دستگاه با استفاده از نخستین برنامهی ذخیره سازی شده به کار گرفته شد. این کار با شکستن عدد به اجزاء و فاکتورهای اولیهی آن انجام شد.
 این ماشین مشخصات نظری ماشین تورینگ را داشت (که در اعداد قابل محاسبه توصیف کردیم) اما بر طبق طرح او ساخته نشده بود. به هر حال تورینگ با شور و حرارت زیادی به توسعهی توانایی اصلی آن ادامه داد. او مدارهای ورودی و خروجی برای سختافزار آن را طراحی کرد و حتی تقاضا کرد که از بلتچلی چاگر ماشین رمزگذاری آلمانی را بیاورند. تورینگ ساعتهای طولانی و سختی را صرف تجزیه و تحلیل ریاضی میکرد، در حالی که معمولاً میتوانست مسایل را با جرقههای دید غریزی خود حل کند.
این ماشین مشخصات نظری ماشین تورینگ را داشت (که در اعداد قابل محاسبه توصیف کردیم) اما بر طبق طرح او ساخته نشده بود. به هر حال تورینگ با شور و حرارت زیادی به توسعهی توانایی اصلی آن ادامه داد. او مدارهای ورودی و خروجی برای سختافزار آن را طراحی کرد و حتی تقاضا کرد که از بلتچلی چاگر ماشین رمزگذاری آلمانی را بیاورند. تورینگ ساعتهای طولانی و سختی را صرف تجزیه و تحلیل ریاضی میکرد، در حالی که معمولاً میتوانست مسایل را با جرقههای دید غریزی خود حل کند.کار کردن با این غول ماشینی در حال پیشرفت، کاری شاق و طاقتفرسا بود. بنا به گفتهی دستیار تورینگ: اپراتور با شروع به کار در اتاق ماشین، مهندس را با خبر میکند و سپس از کلیدهای دستی برای ورود به برنامهی ورودی استفاده میکند... وقتی این منظور برآورده شد، اپراتور از پلهها بالا میرود و نوار را در دستگاه خواننده قرار میدهد و دوباره به اتاق ماشین بر میگردد. اگر ماشین شروع به خواندن نوار کند و دستورات را به درستی اجرا کند، اپراتور مهندس را خبر میکند تا جریانی را روشن کند که کار نوشتن را فعال میکند. مادامی که این طرح روی مونیتور نشان داده میشود که ورودیها پایان پذیرفته است، مهندس کلید جریان نوشتن را خاموش میکند... معمولاً تلاش زیادی لازم است تا نواری را وارد کنند، هر دفعه لازم است تا به اتاق نوار بروند. تورینگ از این موفقیت بسیار خوشحال بود.
علی رغم چنین سختیهایی، ماشین فوق خیلی زود به ماشینی تبدیل شد که کارهای پیچیدهی بیشتری را عهدهدار شود. لامپ تصویر آن میتوانست تا 128 و 40 بیت کلمه را ذخیره کند. گروههایی از ارقام دوتایی شامل دستوراتی بود که کامپیوتر میتوانست انجام دهد. این کامپیوتر نه تنها نخستین مورد عملیاتی بود، بلکه به ظن قوی نخستین مورد دارای هدف سازندهی گسترده بود. چند وقت بعد این دستگاه برای محاسبهی طرح راه دریایی س ت لورنس استفاده شد که یکی از بزرگترین عجایب مهندسی قرن بیستم بود.
به هر حال، دستگاههای اولیه فواید کمتری داشتند. تورینگ علاقهمند بود تا بازی شطرنج را به آن آموزش دهد و ساعات خوشی را با این کار سپری کند. او در جستوجوی روشهای بهبود استراتژی بازی دستگاه بود. با دیدی که قائم مقام داشت، اعضای دیگر این گروه دربارهی محدود کردن ماشین خودکار دیجیتال منچستر به کارهای عقلی خوشنود نبودند و حتی خود را درگیر خطرات آن نمیکردند.
کامپیوتر دانشگاه منچستر
در این نمونه دستگاه فوق ترجیح داد تا خود را کامپیوتر دانشگاه منچستر بخواند و دربارهی رابطهای حرف بزند که برای زیگموند فروید خوشایند باشد.شطرنج بازی کردن ماشین دیجیتال خودکار منچستر از علایق تورینگ بود. به عبارت دیگر: «ماشینآلات هوشمند» یا چنان که معروف شد: «هوش مصنوعی».
تورینگ ایدهاش را در چند مقاله نوشت. مهمترین آنها هوش و ماشینآلات محاسبه بود که در سال 1950 میلادی منتشر کرد. تورینگ در آن تأکید کرد که کامپیوترها میتوانند آموزش ببینند تا برای خودشان فکر کنند. آنها واقعاً میتوانند فکر کنند. مخالفت گسترده با این ایده سبب شد تا آن را یک ایدهی تخیلی نامگذاری کنند. به طوری که فرایندهای کامپیوتر را میتوان به تنوع هوش انسانها تشبیه کرد. تورینگ اظهار داشت که این درهم آمیختگی، عنصری تصادفی مانند چرخ رولت است.
بسیاری از اعتراضات فلسفی، بیهوده و کسل کننده به نظر میرسیدند. او آرزو نداشت تا سؤالی از هوش کامپیوتر بپرسد که سؤالات مربوط به ارادهی آزاد، اخلاقیات، تعریف زندگی و غیره را متوقف نماید. بنابراین او با هوشمندی چنین مواردی را دور میزد. یک راه وجود دارد که بگوییم آیا ماشینی هوشمند است یا نه: آن را پشت صفحهی نمایشگر قرار دهیم و اجازه دهیم یک نفر از آن سؤال کند. سپس بر مبنای پاسخهای نوشته شده تصمیم بگیرد که آیا با موجودی هوشمند رو به روست یا صرفاً با یک ماشین سر و کار دارد. آیا ماشین میتواند انسان را چنان فریب دهد که فکر کند. با انسان دیگری رو به رو شده است؟ تورینگ این بازی تقلیدی را پیشنهاد کرد، که امروزه به آزمون تورینگ معروف است.
تورینگ نشان داد که چطور شخص سؤال کنندهی ماهر میتواند تحقیق کند، تصمیم بگیرد و داوریهای ظریفی داشته باشد و احتمالاً پاسخهای عاطفی بگیرد یا این که جواب خود را از مطالب مکتوب به دست آورد. اما تورینگ روی هم رفته از اعتراضات فلسفی اجتناب نکرد (او صرفاً موارد غیرخلاق و موضوع را دور زد). بحثهای فلسفی خودش زیاد بودند مگر آن که غیر قابل پاسخ دادن باشند. او تأکید داشت که بازی تقلیدی را باید به صورت معیار اساسی پذیرفت. چرا؟ زیرا چگونگی واکنش ما را در برابر یک دیگر نشان میدهد. ما روشی فوری در دست نداریم که بگوییم آیا شخص دیگری هوش دارد یا ندارد. فقط میتوانیم با مقایسهی آنها با خودمان ببینیم که آیا آنها فکر میکنند. و آگاهند؟ تورینگ دلیلی نداشت که چرا نگرش ما در برابر کامپیوتر نباید یکسان بماند. او میپرسد: چرا به انسان نسبت به کامپیوتر باید به شکل متفاوتی توجه شود. (حقیقت این است که این سؤال را مردی میپرسد که خودش را کامپیوتر قلمداد میکند و تعدادی سؤالات جذاب را میگشاید. آیا انسان دیگری بیرون وجود دارد که به من گوش بدهد؟)
تورینگ سخاوتمندانه نقطهنظر انسانی را پذیرفت حتی تا جایی پیش رفت که تعدادی از اعتراضات به بحثش را اظهار میداشت. جدیترین آنها امروزه پس از همکارش ببیج به اعتراض بانو لاولیس معروف است. او نخستین بار آن را بیان کرد. بانو لاولیس متقاعد شده بود که کامپیوترها نمیتوانند اندیشهای از خود داشته باشند، زیرا فقط کاری را میتوانند انجام دهند که به آنها گفته شده است. به عبارت دیگر کامپیوترها فقط کارهایی را انجام میدهند که به آنها به شکل برنامه داده شده است.
پاسخ تورینگ در حد و حدود کامپیوتر بود. وقتی کامپیوتری را برنامهریزی میکنیم، چارچوبی کلی را به آن میدهیم تا انجام دهد اما تمام ابعاد آن را نسنجیدهایم. در مقایسه، دیدهایم که ریاضیات یک بار به صورت مفهومی ساده از اعداد و چند برنامهی ساده محسوب میگردد چنان که بتوان آن را به کامپیوتر تزریق کرد، در حالی که الزامات این سیستم هر چیزی را به صورت ساده بیان کرده است. در حقیقت، آنها نه تنها همه چیز را به طور کاملی اثبات کردهاند بلکه ناهماهنگی خود را هم بهبود بخشیدهاند. چنان که اهرنوارد مشاهده کرد: مواقعی وجود دارد که به نظر میرسد حتی ریاضیات هم هدف خودش را دارد.
چنین افکاری سرانجام تورینگ را به ورای حوزهی کامپیوتر و به ریختزایی سوق داد. این پیشرفت با رشد سازوارههای موجودات زنده ربط دارد. تورینگ گفت که در عین حال، همانند ریاضیات هر سیستم سادهای به پیچیدگی میانجامد. ساختار متقارن، هم شکل با گسترش شکل آن در ساختاری غیر متقارن و با الگوی خودش رشد میکند. در سال 1952 میلادی تورینگ نخستین مقاله دربارهی این موضوع را منتشر کرد: «مبنای شیمیایی ریختزایی»
این مقاله این سؤالها را مطرح میکند: گیاهان چطور رشد میکنند؟ مواد چگونه شکل میگیرند؟ ریخت زایی از واژههای یونانی شکل و منشاء، مشتق شده است. تصادفاً، کریک و واتسون در کمبریج در آن هنگام تلاش میکردند تا این مشکل را از نقطه نظر میکروبیولوژی حل کنند و سرانجام به مارپیچ دوگانهی D.N.A رسیدند. اما تورینگ از منظر ریاضیات به این مسئله توجه میکرد. چطور سوپ شیمیایی نسبتاً سادهی زمین به موجودات زندهای با چنین پیچیدگی تبدیل میشود؟ کریک و واتسون به دنبال توضیحی برای چگونگی وقوع آن بودند. تورینگ هم در جستوجوی پاسخی برای چگونگی و چرایی وقوع آن بود. او میخواست پاسخی ریاضی بیابد که الگوی زندگی را بر حسب روشهای ریاضیات توضیح دهد. (اگر اینشتین میتوانست کارکردهای نهایی جهان را بر اساس فرمولهای ریاضیات توضیح دهد، تورینگ در صدد توصیف زندگی به روشی مشابه بود. اگر تورینگ بلند همت نبود، به جایی نمیرسید.)
چگونه سوپ شیمیایی آغازین شامل اطلاعاتی بود که آن را توانا میکرد تا بر پیچیدگی خود بیافزاید؟ در این راستا این سؤال که چگونه کامپیوتر هوش را بسط میدهد، آشکار است. اما این مسایل با ریاضیات چگونه حل میشدند؟ نمونههای متعددی را میتوان در نظر گرفت. محلول شیمیایی غیر آلی اشباع شدهای را که در آن بلورها در حال شکل گرفتن یا رشد است در نظر بگیرید. این چیزی است که به نظر میرسد انجام میشود، یعنی به شکل نامتقارن و مرموز و به شیوهای «زنده» رشد مییابد. در سطح شیمیایی برای هرگونه عدم تقارن توضیحی وجود ندارد اما در سطح مولکولی، حرکات فردی و تصادف مولکولها در محلول تصادفی است. بنابراین تعجبی ندارد که این بلورها به شیوهی نامتقارنی شکل میگیرند. از جهتی، پیچیدگی در همان لحظهای رخ میدهد که خلق میشود. مثالی روشنگر از این فرایند در موسیقی مدرن دیده میشود. آهنگساز مجارستانی جرج لیگتی قطعهای متشکل از 100 مترونوم نوشته است و همه با سرعتهای متفاوتی تنظیم شده است. همهی مترونومها بیدرنگ شروع میشوند و سپس از دور خارج میشوند. این صداها مانند برنامهای برای آشفتگی است، اما چیزی که در حقیقت رشد میکند موسیقی واقعی و عجیب است که به یک معنی مترونومها آنها را خلق میکنند.
تورینگ متقاعد شده بود که پیشرفتهای ریاضی مشابهی در طبیعت رخ داده است. گلها، گیاهان و سلولهایی که او مورد مطالعه قرار داد، همه الگوهای پیشرفته و در معرض دیده بودند. بسیاری از آنها دنبالههای ریاضی شگفتانگیزی را نشان میدهند.
برای نمونه مارپیچ مخروط صنوبر و دانههای متراکم گل آفتابگردان بازتابی از دنبالهی فیبوناچی است. این دنباله عبارت است از 21،13،8،5،3،2،1،1.... که هر عددی جمع دو عدد قبلی است. ویژگیهای حیرتآور و مرموز اعداد فیبوناچی، در ریاضیات (مثلثهای فیثاغورثی، اعداد اول و حد اعتدال همه مرتبط با آن است) و در طبیعت (آناناس، رشد برگها و مسافت سیارات از خورشید همه نشان دهندهی ویژگیهای فیبوناچی است) وجود دارد.
در طبیعت، طرحها عمیقاً به ریاضیات مربوط میشود. آیا امکان دارد که چیزی در ماهیت ریاضیات پیشرفت چنین پیچیدگیهایی را کنترل کند؟
اینها سؤالاتی بودند که در دههی 1950 میلادی ذهن تورینگ را به خود مشغول کرده بود. او در حین مطالعات پیچیده به استفاده از ماشین دیجیتال خودکار منچستر ادامه داد، در حالی که توسعهی عملی کامپیوتر را رها کرده بود. کامپیوتر جدید باید کارهایی بیشتر از نوشتن نامههای عاشقانه انجام دهد.
در آن زمان تورینگ خانهای در ویلمسلو، حومهای زیبا در حاشیهی منچستر خریده بود. او در سال 1951 میلادی به شکلی استثنایی در سن 39 سالگی به عضویت انجمن سلطنتی انتخاب شد. یکی از معرفهای او فیلسوف برتراند راسل بود. او یکی از نخستین کسانی بود که اهمیت کار فلسفی تورینگ را تا حد زیادی شناخته بود. این جنبهی کار او تقریباً نیم قرن بعد از آن باید دقیقاً مورد کاوش قرار گیرد.
تورینگ 12 ساعت ممتد در آزمایشگاه به کار مشغول بود و عادت داشت تا ماشین دیجیتال خودکار منچستر را تمام شب سهشنبهها و پنجشنبهها رزرو کند.
او در آن زمان تلاش میکرد تا به این سؤال که دربارهی مبنای شیمیایی ریختزایی روبه رو بود بپردازد. اما تورینگ متوجه شد در تغییراتی کوچک که به نظر میرسید در سیستمهای معادلات دیفرانسیل موجب عدم تقارن میشود، گیر کرده است. به نظر میرسد که وقتی پیچیدگی خودش را خلق کرد، اینها دلیلی برای نظریههای شیمیایی ریختزایی بودند. پیچیدگی خودش را خلق میکند، موضوعی کاملاً پیچیده است.
تورینگ متوجه شد که همهی این موارد در ارتباط با فرضیهی ریمان، به مأیوس کنندگی مطالعهی شکست خوردهی اعداد اول بودکه برای پی. اچ. دی خودش کار میکرد. مانند قبل، چشمههای اولیهی الهام در بیابان محاسبات خشک شد و یک بار دیگر احتمال خودکشی بالا گرفت.
این دفعه منظرهی خودکشی برایش جذاب بود. کار او تمام شده بودو علیرغم ویژگیهای منحصر به فردی که داشت، از انجام همهی کارهای خلاق با کامپیوترها باز مانده بود.
تورینگ تصمیم نهایی را گرفت، او لااقل یک بار برای آن آموزش دیده بود. آلن تورینگ در شب هفتم ماه ژوئن سال 1954 میلادی طبق عادت قبل از خواب سیب خورد و خوابید، تورینگ سیب را به سیانور آغشته کرده بود.
سخن پایانی
تورینگ بعد از مرگش از یاد رفت و نادیده گرفته شد. کار او در زمان جنگ روی کلوسس به صورت سری باقی ماند. محرومیت نهایی او از کارهای خلاقانهی عملی روی کامپیوترهای اصلی بریتانیا به این معنی بود که قهرمانان فراموش میشوند. ارزش کار نظری درخشان او را تنها اهل فن میشناسند.اما وقتی اندرو هاجز در سال 1985 میلادی زندگی نامهی کامل و روشنگر تورینگ را نوشت، سبب شد تا معرفی گستردهای از او انجام شود. علیرغم تحقیقات جامع، تورینگ برای هاجز مانند هم عصرهایش به شکل یک معما باقی ماند. با این همه موفقیتهای تورینگ برای همگان حرف میزند. او پیشاهنگ تئوری کامپیوتر شناخته شد. او پدر کامپیوتر جدید و مردی است که سبب پیروزی در جنگ شد. او نخستین کسی بود که به شکلی جامع سؤالاتی دربارهی هوش مصنوعی و ریختزایی مطرح کرد، سؤالاتی که تا امروز بدون جواب به قوت خود باقی مانده است.
تقویم تاریخ کامپیوتر
4000 سال پیش از میلاد شکلهای سادهای از چرتکه در چین و بابل استفاده میشد.
قرن اول پیش از میلاد تنها ماشین حساب کشف شدهی مربوط به این دوره، هم چنان مرموز باقی مانده است.
1623 میلادی شیکارد ساعت حسابگر را در توبینگن ساخت که آن را نخستین کامپیوتر دیجیتال شناختهاند.
1630 میلادی اوترد خطکش محاسبه را اختراع میکند. بسیاری از دانشمندان گفتهاند که این نخستین کامپیوتر آنالوگ است
1642 میلادی پاسکال ماشین حساب ممتازی را اختراع میکند که میتواند با عدد 8 رقمی کار کند.
1673 میلادی لایب نیتز ماشین حساب سادهتر و تواناتری اختراع میکند که میتواند جزر را محاسبه کند
اوایل قرن نوزدهم نساج فرانسوی ژاکارد، کارتهایی تولید میکند که طرحهای بافندگی را روی دستگاه بافندگی کنترل میکند. این نخستین برنامهی ماشین است.
1823 میلادی ببیج کارش را روی موتور تفاضل شماره 1 شروع میکند.
1854 میلادی بول مقالهای دربارهی منطق دوتایی منتشر میکند.
1896 میلادی هولریس از ماشین کارتخوان برای سرشماری آمریکا استفاده میکند.
1937 میلادی تورینگ مقالهای دربارهی اعداد قابل محاسبه منتشر میکند و محدودهی نظری کامپیوترهای آینده را ترسیم میکند.
1948 میلادی ماشین دیجیتال خودکار منچستر نخستین کامپیوتر دیجیتال برنامهریزی شدهی الکترونیک است که وارد عرصهی عمل میشود.
منبع مقاله :
جمعی از نویسندگان زیرنظر شورای بررسی، (1394)، آشنایی با مشاهیر علم، تهران: نشر و تحقیقات ذکر، چاپ اول


























