رساله‌ی چهار ضلعی

یکی از بزرگ‌ترین نمایندگان علم اسلامی یقیناً نصیرالدین طوسی است (672- 597ق/ 1273-1200م). او دانشمندی جامع بود و فکری نسبتاً بدیع داشت و به همه‌ی علوم زمان خود وارد شد، در آن‌ها تحقیق و تعمق کرد و در این کار مهارتی نشان داد که موجب شهرت فراوان او بین مسلمین گردید. خوندمیر داستان این را که چگونه وی مورد بی مهری خلیفه المستعصم قرار گرفت و در خدمت هلاکو وارد شد و او را علیه بغداد برانگیخت، حکایت کرده است. هلاکو و فرزند او خواجه نصیر را مورد لطف خود قرار دادند. آنان رصدخانه‌ی مراغه را برای او بنا و آن را با شکوه و جلال مجهز کردند و در آنجا بود که زیر نظر خواجه نصیر زیج ایلخانی تهیه و مدون شد. این دانشمند عالیقدر از خود آثاری متعدد و مهم و متنوع به یادگار گذاشت که اروپائیان تقریباً از همه‌ی آن‌ها بی خبراند.(1)
ما فکر نمی‌کنیم که ممکن باشد بین آثار خواجه نصیر کتب زیادی یافت شود که به اندازه این رساله‌ی چهار ضلعی (2) فایده داشته باشد. نسخه‌ی خطی کاملاً عربی که از روی آن این کتاب چاپ شده است. نام مؤلف ندارد، اما عنوان آن در برخی از فهرست‌های آثار خواجه نصیر هست. علاوه بر این در آغاز کتاب گفته شده است که مؤلف پس از آنکه کتاب را به فارسی نوشت خود او را به عربی ترجمه و این ترجمه را در سال (658ق/ 1260م) تمام کرد. همین نشانه‌های ساده به وجهی بسیار قوی نسبت این کتاب را به خواجه نصیر تأیید می‌کند.
ما توانستیم این نسخه‌ی خطی را در نزد جناب ادهم پاشا که امروزه مالک آن است مشاهده کنیم. تاریخ ]کتابت[ آن 677ق. است و بسیار خوب مانده و خط آن عالی است و ظرافتی جالب دارد و برای خواندن خط آن حوصله و دقت بسیار باید به کار رفته باشد.(3) شکل‌های هندسی متن عربی که با خطوط بسیار نازک رسم شده و عده‌ی آن‌ها زیاد است، کاملاً عاری از سهو و خطای علامتگذاری نیستند که البته احتراز از آن خطاها برای نسخه نویسانی که این قبیل نوشته‌ها را نقل می‌کنند بسیار مشکل است، اما این نقص کوچک ارزش یک نسخه‌ی خطی نادر و شاید منحصر به فرد را کم نمی‌کند؛ به خصوص که این نسخه علاوه بر ظرافت مادی، از حیث اطمینان بر صحت متن دارای این امتیاز است که ] تاریخ کتابت آن [ تقریباً معاصر با مؤلف رساله می‌باشد.
موضوع و کیفیات خاصی به این نوشته ارزش زیادی می‌دهند. موضوع این رساله احصاء شکل‌های سه ضلعی و چهار ضلعی مرسوم در صفحه یا بر سطح کره و نسبت‌های بین آن‌ها و دستورهای مثلثاتی حاصل از این نسبت‌ها و همچنین دستورهایی است که مؤلفان معاصر به طریق تازه به دست آورده اند و بالاخره حل مثلثات. کیفیاتی که موجب امتیاز این رساله می‌شوند، بدعت و تازگی روش و وحدت تألیف و دقت است که در نزد ریاضیّون شرقی کمیاب است که قضایا را به کسانی که آن‌ها ] را[ اختراع کرده اند نسبت دهند.
این رساله شامل پنج مقاله است. در مقاله‌ی اول که در واقع نوعی مقدمه است، تعاریف و قضایای مربوط به نسبت مرکب (4) یعنی نسبتی که مساوی با حاصل ضرب دو نسبت دیگر است، بیان می‌شوند. در مقاله‌ی دوم دوازده شکل مختلف چهار ضلعی مسطح مورد بحث قرار می‌گیرند و در این باب طرز پیدا کردن نسبت‌های بین دوازده پاره خطی که به رئوس آن‌ها ختم می‌شوند، ذکر شده است و سه طریق برای انتخاب شش پاره خط از این‌ها را که به سه طریق مختلف می‌توان آن‌ها را اختیار کرد تا یک نسبت مرکب تشکیل دهند، بیان شده است. پس از آن، اثبات سه نوع نسبت که به این نحو به دست می‌آیند داده شده و این استدلال‌ها از روی خطوط متوازی که از رأس‌های چهار ضلعی رسم ]می‌شوند[ و مثلث‌های متشابه پدید می‌آورند، صورت گرفته است. این بحث که بسیار منظم و بسیار کامل است، بالاخره منتهی به این می‌شود که استدلال چنین نسبتی را که بطلمیوس بیان کرده، از نو گرفته و آن را به همه‌ی حالات دیگر تعمیم دهد. در این رساله ترقی جالب توجهی در فکر تعمیم قضایا که فوق العاده در علوم ریاضی لازم است، دیده می‌شود. با این حال هنوز بحث نصیرالدین تا اندازه ای مبهم و دشوار به نظر ما می‌آید. در تحقیق عده‌ی حالات ممکن، بیهوده گی‌هایی (5) دیده می‌شود. مؤلف رساله عده‌ی نسبت‌هایی را که از بحث در چهار ضلعی پیدا می‌شود به 497664 گونه نسبت تخمین می‌زند و قید می‌کند که در این عده بسیاری از نسبت‌ها تکرار می‌شوند و البته این قید و تحدید، ارزش و فایده‌ی تخمین مؤلف را از بین می‌برد. با این حال در کار نصیرالدین ترقی و پیشرفت انکار ناپذیر است؛ زیرا از دو راهی پیچ و خمی که موجب گمراهی پیشقدمان او بوده عبور کرده است. در مقاله‌ی سوم روش حل مثلث‌های مسطح به اختصار بیان شده و دستور تناسب جیب زوایا با اضلاع مقابل آن‌ها داده شده و چگونگی تبیین دو قوس متوالی در یک دایره در صورت معلوم بودن مجموع آن‌ها و نسبت سینوس آن‌ها تعیین گردیده است. در مقاله‌ی چهارم مؤلف چهار ضلعی کروی را که از تقاطع چهار دایره‌ی عظیمه پیدا می‌شود، مورد مطالعه قرار می‌دهد و در این باب همان روشی را که در چهار ضلعی مسطح پیروی کرده بود به کار می‌برد. از بیست و چهار قوس که از تقاطع چهار دایره عظیمه پیدا می‌شوند، او شش قوس را به وجوه مختلف انتخاب و بین جیب‌های آن‌ها وجود رابطه‌ی مرکب را نشان می‌دهد. ]وی[ برهان بطلمیوس را که فقط در یک حالت برقرار شده کنار می‌گذارد و استدلال دیگری که اسلوبی تر و همراه با بحث دقیقی از حالات مختلف است، می‌دهد.
در همه‌ی این مقالات کار نصیرالدین فقط این است که با مهارت و زبردستی، نتایجی را که از علم عتیق حاصل شده تعمیم می‌دهد و خاصیت‌هایی را که بطلمیوس و قبل از او منلائوس به کار برده بودند، توسعه می‌بخشد. در مقاله‌ی پنجم که بسیار از مقاله‌های دیگر رساله مهم تر است، او طرقی را که معاصران سعی کرده بودند که به جای طرق قدیم برای توفیق در حل مثلث‌های کروی به کار برند، بیان می‌کند. در زمان وی دو طریق معمول بوده است؛ طریق اول که اصل آن را می‌توان در آثار بطلمیوس و منلائوس یافت در نزد مسلمین توسط سه مهندس تکمیل شده بود: ابونصر علی بن عراق، ابوالوفاء بوزجانی و ابو محمد خجندی. این طریق مبنی بر این است که دو مثلث کروی ABC و A´B´C´ که زوایای B و B´ آن‌ها قائمه باشد و دو زاویه‌ی A از آن‌ها مشترک یا متقابل به رأس باشند، در نظر می‌گیرد. از این شکل نسبت 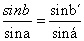حاصل می‌شود که اگر در آن b´ را مساوی ربع دایره بگیریم، به صورت 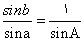در می‌آید. چندین استدلال از این دستور در این رساله دیده می‌شود: سه استدلال از ابونصر و یک استدلال از ابوالوفاء و یک استدلال از ابومحمود (خجندی) و یک استدلال دیگر که آن را فضل بن حاتم نیریزی (ابوالعباس) و ابوجعفر خازن استعمال کرده اند و یک استدلال که از همه به طور قطع ظریف تر است و آخرین استدلال در رساله‌ی مورد بحث است، از قاعده‌ی شش مقدار (6) استخراج شده است. از همین دستور، فرمول 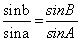در مورد مثلث کروی دلخواه به دست می‌آید و از این رو در حالت مثلث قائم الزاویه، دو رابطه‌ی دیگر 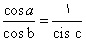و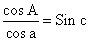 نتیجه می‌شود.
روش دومی را که معاصران تتبع کرده اند و افتخار آن از ابوالوفاء بوزجانی است، مبنی بر استفاده از ظلّ یا تانژانت است. از شکل طریق قبل که آن ]را] به وجه دیگری در نظر می‌گیرند، دستور خاص این شکل یعنی sin c = 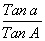پیدا می‌شود. این دستور در رساله‌ی مورد بحث به چندین طریق به اثبات رسیده که یکی از آن‌ها که بسیار ظریف است از قاعده‌ی شش مقدار به دست می‌آید. این دستور را در مورد مثلث‌های کروی دلخواه نمی‌توان به کار بست و از این دستور روابط زیر در مثلث کروی که زاویه‌ی B از آن قائمه باشد حاصل می‌شود:
Cos A = 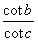، Cos b = ،
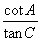مؤلف، این دو طریق را برای حل مثلث‌های کروی قائم الزاویه به کار می‌برد. او مثلث‌های کروی دلخواه را با تجزیه کردن آن‌ها به دو مثلث قائم الزاویه حل می‌کند و یا اینکه یکی از رأس‌ها را قطب قرار داده، دایره‌ی عظیمهای رسم می‌کند که با امتدادِ اضلاع مثلث قائمالزاویهای تشکیل می‌دهد.
مؤلف اظهار می‌دارد که نمی‌توان طریق ظلّ‌ها را در حالتی که سه معلوم مسئله، در حالت مثلث دلخواه، سه ضلع یا سه زاویه باشند، به کار برد. بالاخره نصیرالدین از این طریق در مقابل ریاضیّونی که تصور می‌کردند که ترقی سریع ظلّ‌ها (تابع) مانع استعمال آن‌ها می‌شود، دفاع می‌کند و برای این دفاع نشان می‌دهد که با استفاده از خواص آن‌ها همواره می‌توان مسئله را منجر به آن کرد که فقط قوس‌های کوچکتر از 45 درجه به کار روند.
شاید سهم نصیرالدین در این تألیف ناچیز (7) باشد، اما او لااقل با بیانی که حاکی از هنر واقعی وی در تدوین مطالب و با فکر تألیفی ای که واقعاً علمی است، کارهای پیشقدمان خود را جمع آوری کرده است. ما تاکنون نمی‌دانستیم که هندسه چه ترقی حقیقی‌ای در زیر دست مسلمین پیدا کرده است و این رساله به این قسمت از تاریخ علم روشنایی زیادی می‌بخشد. این رساله‌ی علمای اسلامی را از قرن سیزدهم به بعد مالک طرقی ای نشان می‌دهد که خود ایجاد کرده بودند و می‌توانستند با شجاعت آن‌ها را در مقابل طرق قدما طرح کنند و بنا براین به ما نشان می‌دهد که علمای اسلامی در مثلثات روشی کاملاً شبیه روش خودمان به کار می‌بستند؛ یعنی مسائل عمومی حل مثلث‌ها را طرح می‌کردند و به آن‌ها با فرمول‌هایی که هم اکنون به کار می‌بریم، جواب می‌دادند. با این حال، اکتشافات آنان به غرب وارد نمی‌شود و دانشمندان رنسانس مجبور بودند که خود به کشف آن‌ها بپردازند.(8)

پی‌نوشت‌ها:

1. این مقاله در باره‌ی رساله‌ی کشف القناع عن اسرار القطّاع تألیف نصیرالدین طوسی است که تحریر عربی آن توسط الکساندر پاشا کاراتئودوری در سال 1891 م به همراه ترجمه‌ی فرانسوی آن به چاپ رسید. این مقاله را کارادوو (B. Carra de Vaux) در جلد بیستم، دوره‌ی هشتم روزنامه‌ی آسیایی در خلال ماه‌های ژوئیه و اوت سال 1896 م. منتشر کرد. [این ترجمه در میان آثار بازمانده از شادروان ابوالقاسم قربانی، که در پژوهشکده‌ی تاریخ علم دانشگاه تهران نگاهداری می‌شود یافت شد. - و.]
2. منظور از چهارضلعی «شکل قَطاع» است. قضیه‌ی معروف منلائوس در ریاضیات و نجوم دوره‌ی اسلامی «شکل قطّاع» نام گرفت.
3. ]منظور مصحّح کتاب یعنی کاراتئودوری است.- م [.
4. ]منظور«نسبت مؤلفه» است.و [.
5. puérilité.
6. ]النسبة المؤلّفة- و[.
7. محدود.
8. بعد از این در چند سطر کارادوو از توزیع و نشر کننده‌ی این رساله تقدیر می‌کند. ژنو 22 آذرماه 1343: - م .

منبع مقاله :
معصومی همدانی، حسین؛ (1391)، استادبشر (پژوهش‌ها‌یی در زندگی، روزگار، فلسفه وعلمِ خواجه نصیر الدّین طوسی)، تهران: میراث مکتوب، چاپ اول