نویسنده: والدک مِین ویل (1)
ترجمه: مهران اخباریفر
ترجمه: مهران اخباریفر
کسرها در قدیمی ترین اسناد ریاضی یافته شده وجود دارند. اما ملل باستان، رهیافتی عمومی برای کار با کسرها نداشتند و در نتیجه، روش های خاص کار با کسرها اغلب محدودیتهایی در کاربرد آن ها ایجاد می کرد.
بابلی ها از 2000 سال پیش از میلاد از کسر استفاده می کردند. این کسرها به شکل ارزش مکانی نوشته می شدند و اساساً همانند کسرهای اعشاری امروزین بودند؛ اما مخروج ها، که نوشته نمی شدند، توان های متوالی شصت بودند و جداکننده ای که متناظر با ممیز اعشاری باشد وجود نداشت.
پاپیروس رایند، که گاهی پاپیروس احمس هم نامیده می شود، حاوی اولین برخورد نظام مند با کسرهای واحد است. کسرهایی را که نمی شد فقط با یک کسر واحد نمایش داد، به صورت مجموع دو یا چند کسر واحد نمایش می دادند ولی بین آن ها به جای علامت جمع فقط فاصله می گذاشتند. مثلاً 2/35 به صورت 1/42[+]1/30 نشان داده شده است. کسرهای واحد با یک نماد کسر که مخرج زیر آن قرار گرفته است نمایش داده شده اند. در هیروگلیف (نوشتار تصویری)، 1/4 به صورت ### و 1/13 به صورت ### نوشته می شد. کسر 2/3 با نماد خاص ### و 1/2 گاهی با نماد ### نوشته می شد. در هیراتیکِ شکسته، کسرهای واحد را با یک نقطه یا نماد دیگری به نام رو (2) که روی مخرج می گذاشتند نشان می دادند.
یونانی ها نیز اغلب متکی به کسرهای واحد بودند. آنان برای نمایش کسرهای واحد، اغلب مخرج را با یک یا دو علامت تکیه می نوشتند؛ مثلاً برای 1/32. اما ریاضیدانان یونانی خود را با کسرهای واحد محدود نکردند. گاهی کسرهای کلی را با یک بار نوشتن صورت با یک علامت تکیه و دوبار نوشتن مخرج با دو علامت تکیه نمایش می دادند؛ مثلاً،
برای 1/32. اما ریاضیدانان یونانی خود را با کسرهای واحد محدود نکردند. گاهی کسرهای کلی را با یک بار نوشتن صورت با یک علامت تکیه و دوبار نوشتن مخرج با دو علامت تکیه نمایش می دادند؛ مثلاً، . در بعضی موارد، مخرج را جای می نوشتند که ما امروزه نما را قرار می دهیم. در موارد دیگر، مخرج درست بالای صورت نوشته می شد (درست برعکس نماد امروزین ولی بدون خط کسری).
. در بعضی موارد، مخرج را جای می نوشتند که ما امروزه نما را قرار می دهیم. در موارد دیگر، مخرج درست بالای صورت نوشته می شد (درست برعکس نماد امروزین ولی بدون خط کسری).
در روم، کسرها در محاسبات مالی و در اندازهگیری ها کاربرد فراوان داشتند. هر کسر نامی خاص داشت و رومی ها معمولاً مخرج کسر را مقدار ثابت 12 می گرفتند؛ این احتمالاً به این دلیل بوده است که سکه ی مسی آن ها، اس (3)، به 12 اونسیا تقسیم می شد. در مدارس روم محاسبات کسری بخش اعظم آموزش حساب را تشکیل می داد.
ظاهراً منشأ شیوه ای امروزینِ نوشتن کسرها هند است. شاید هندی ها این نوع نمایش را از یونان گرفته باشند، چرا که یونانیان در دوره ی متأخر از این شیوه استفاده می کردند. در دست نوشته ی بخشالی (4) (حدود قرن ششم میلادی) کسرها با نوشتن صورت بالای مخرج بدون خط کسری نمایش داده شده اند. اعداد صحیح را به صورت کسرهایی با مخرج 1 نمایش داده اند. خط کسری حدود اوایل قرن یازدهم میلادی توسط مسلمانان به شکل های زیر به کار می رفت:
 اما همه جا از آن استفاده نمی کردند. وقتی که کاهن یهودی، آبراهام بن عِذرا (1907-1167م) شکل مغربی را پذیرفت، معمولاً خط کسری را حذف می کرد، اما در دست نوشته های بعد از آن زمان معمولاً خط کسری وجود دارد.
اما همه جا از آن استفاده نمی کردند. وقتی که کاهن یهودی، آبراهام بن عِذرا (1907-1167م) شکل مغربی را پذیرفت، معمولاً خط کسری را حذف می کرد، اما در دست نوشته های بعد از آن زمان معمولاً خط کسری وجود دارد.
اولین محرّک استفاده از کسرهای اعشاری را سیمون استون در سال 1585 ایجاد کرد؛ ولی باز هم بسط نمادهای مناسب مدتی به طول انجامید و ممیز اعشاری تا ربع اول قرن هجدهم به طور همگانی استفاده نمی شد.
اکثر نویسندگان کتاب های حساب در اروپا، بحث از کسرهای متعارفی و اعشاری را تا آخر کتاب به تعویق می انداختند. احتمالاً از کمتر خواننده ای انتظار می رفت که به کسرها برسد.
واژه عربی کسر به معنی «شکستن» است. سپس شکل های لاتین fractio و ruptus minutum به معنی «اعداد شکسته» توسط اولین نویسندگان اروپایی به کار رفت که واژه ی انگلیسی fraction به معنی «کسر» از همان ریشه است.
دیویس، هارولد؛ (1384)، تاریخ محاسبه، مهران اخباریفر، تهران، انتشارات علمی و فرهنگی، چاپ اول..
بابلی ها از 2000 سال پیش از میلاد از کسر استفاده می کردند. این کسرها به شکل ارزش مکانی نوشته می شدند و اساساً همانند کسرهای اعشاری امروزین بودند؛ اما مخروج ها، که نوشته نمی شدند، توان های متوالی شصت بودند و جداکننده ای که متناظر با ممیز اعشاری باشد وجود نداشت.
پاپیروس رایند، که گاهی پاپیروس احمس هم نامیده می شود، حاوی اولین برخورد نظام مند با کسرهای واحد است. کسرهایی را که نمی شد فقط با یک کسر واحد نمایش داد، به صورت مجموع دو یا چند کسر واحد نمایش می دادند ولی بین آن ها به جای علامت جمع فقط فاصله می گذاشتند. مثلاً 2/35 به صورت 1/42[+]1/30 نشان داده شده است. کسرهای واحد با یک نماد کسر که مخرج زیر آن قرار گرفته است نمایش داده شده اند. در هیروگلیف (نوشتار تصویری)، 1/4 به صورت ### و 1/13 به صورت ### نوشته می شد. کسر 2/3 با نماد خاص ### و 1/2 گاهی با نماد ### نوشته می شد. در هیراتیکِ شکسته، کسرهای واحد را با یک نقطه یا نماد دیگری به نام رو (2) که روی مخرج می گذاشتند نشان می دادند.
یونانی ها نیز اغلب متکی به کسرهای واحد بودند. آنان برای نمایش کسرهای واحد، اغلب مخرج را با یک یا دو علامت تکیه می نوشتند؛ مثلاً
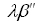 برای 1/32. اما ریاضیدانان یونانی خود را با کسرهای واحد محدود نکردند. گاهی کسرهای کلی را با یک بار نوشتن صورت با یک علامت تکیه و دوبار نوشتن مخرج با دو علامت تکیه نمایش می دادند؛ مثلاً،
برای 1/32. اما ریاضیدانان یونانی خود را با کسرهای واحد محدود نکردند. گاهی کسرهای کلی را با یک بار نوشتن صورت با یک علامت تکیه و دوبار نوشتن مخرج با دو علامت تکیه نمایش می دادند؛ مثلاً،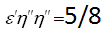 . در بعضی موارد، مخرج را جای می نوشتند که ما امروزه نما را قرار می دهیم. در موارد دیگر، مخرج درست بالای صورت نوشته می شد (درست برعکس نماد امروزین ولی بدون خط کسری).
. در بعضی موارد، مخرج را جای می نوشتند که ما امروزه نما را قرار می دهیم. در موارد دیگر، مخرج درست بالای صورت نوشته می شد (درست برعکس نماد امروزین ولی بدون خط کسری).در روم، کسرها در محاسبات مالی و در اندازهگیری ها کاربرد فراوان داشتند. هر کسر نامی خاص داشت و رومی ها معمولاً مخرج کسر را مقدار ثابت 12 می گرفتند؛ این احتمالاً به این دلیل بوده است که سکه ی مسی آن ها، اس (3)، به 12 اونسیا تقسیم می شد. در مدارس روم محاسبات کسری بخش اعظم آموزش حساب را تشکیل می داد.
ظاهراً منشأ شیوه ای امروزینِ نوشتن کسرها هند است. شاید هندی ها این نوع نمایش را از یونان گرفته باشند، چرا که یونانیان در دوره ی متأخر از این شیوه استفاده می کردند. در دست نوشته ی بخشالی (4) (حدود قرن ششم میلادی) کسرها با نوشتن صورت بالای مخرج بدون خط کسری نمایش داده شده اند. اعداد صحیح را به صورت کسرهایی با مخرج 1 نمایش داده اند. خط کسری حدود اوایل قرن یازدهم میلادی توسط مسلمانان به شکل های زیر به کار می رفت:
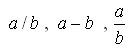
اولین محرّک استفاده از کسرهای اعشاری را سیمون استون در سال 1585 ایجاد کرد؛ ولی باز هم بسط نمادهای مناسب مدتی به طول انجامید و ممیز اعشاری تا ربع اول قرن هجدهم به طور همگانی استفاده نمی شد.
اکثر نویسندگان کتاب های حساب در اروپا، بحث از کسرهای متعارفی و اعشاری را تا آخر کتاب به تعویق می انداختند. احتمالاً از کمتر خواننده ای انتظار می رفت که به کسرها برسد.
واژه عربی کسر به معنی «شکستن» است. سپس شکل های لاتین fractio و ruptus minutum به معنی «اعداد شکسته» توسط اولین نویسندگان اروپایی به کار رفت که واژه ی انگلیسی fraction به معنی «کسر» از همان ریشه است.
پی نوشت ها :
1.Waldeck E. Mainville/Jr
2. ro
3. s. a
4. Bakhshali
دیویس، هارولد؛ (1384)، تاریخ محاسبه، مهران اخباریفر، تهران، انتشارات علمی و فرهنگی، چاپ اول..


























