مترجم: حسین معصومی همدانی
(در اروپای قرون وسطی به Albateneius و Albategni و Albategnius معروف بود)
بَتّانی که از بزرگترین منجمان اسلامی است، به احتمال زیاد پیش از سال 858/244 در شهر حَرّان یا نزدیک آن، در شمال غربی بین النهرین، متولد شد؛ و از همین رو است که او را حرانی می خوانند. از دو نسبت دیگر، نسبت رَقّی، که فقط در فهرست ابن ندیم (1) آمده، اشاره به شهر اَلرَّق در ساحل چپ فرات دارد که بَتّانی بیشتر عمر خود را در آن گذراند و در همان جا رصدهای معروف خود را انجام داد؛ و نسبت صابی دلالت بر آن دارد که اجداد او به کیش صابیان حران بوده اند (2) (خود او، چنان که از نام محمد و کنیه ی ابوعبدالله بر می آید، مسلمان بوده است). مذهب صابی حافظ مقدار معتنابهی از ستاره پرستی و ستاره شناسی بین النهرین قدیم بود، و چون حکام مسلمان با آن مدارا می کردند تا اواسط قرن پنجم/ یازدهم باقی ماند. یکی از چیزهایی که به توجه به نجوم حتی در این دوره اخیر از ستاره پرستی بین النهرین دلالت دارد این است که ریاضیدان و منجم بزرگ ثابت بن قره که معاصر بَتّانی و از او سالمندتر بود (901-835/ 288-221). از همین ناحیه برخاسته بود و کیش صابی داشت. در مورد منشأ نسبت بَتّانی هیچ توضیح قانع کننده ای نمی توان داد. خولسون (Chwolsohn) حدس زده است (3) که این کلمه از نام شهر قدیمی بَثنه (یا بَتنه، به یونانیΒατναι، و به سریانی بَطنان) در نزدیکی شهر قدیمی اَلرُّها مشتق شده است، اما نلینو این حدس را رد کرده (4) و استدلال او که کاملاً مجاب کننده است این است که امکان ندارد «ط» سریانی به «ت» عربی (بَطنان به بَتّان) تبدیل شود، و چون شاهدی که بر وجود شهر یا قصبه ای به نام بتان دلالت کند در دست نداریم، نلینو می گوید که این لفظ نام محله یا کوچه ای در شهر حران بوده است.درباره تاریخ دقیق تولد بَتّانی و کودکی او چیزی نمی دانیم، و چون او نخستین رصد خود را در سال 877/264 انجام داده، نلینو تاریخ تولد او را پیش از سال 858/244 می داند، پدر او، به احتمال زیاد، جابر بن سنان حرانی بود که کارش ساختن آلات نجومی بود و ابن ندیم نام او را در کتاب خود آورده است(5)، و این نکته نه تنها علت توجه شدید فرزندش را به نجوم، بلکه دلیل مهارت او را در طرحریزی آلات جدید نجومی، مثلاً یک نوع جدید از ذات الحِلَق، معلوم می سازد.
در مورد بقیه ی زندگی بَتّانی هم اطلاعات ما ناقص است. به گفته ابن ندیم در فهرست (6) و ابن قفطی در تاریخ الحکما (7)، بَتّانی
... از رصادان مشهور و در هندسه و نجوم نظری و عملی (محاسباتی) سرآمد اقران بود. زیج مهمی تألیف کرد که حاوی رصدهای خود او از نیّرین (خورشید و ماه) است و حرکات این دو سیاره را که در مجسطی بطلمیوس آمده است، اصلاح کرده است همچنین در این کتاب او حرکات پنج سیاره دیگر را هم بر پایه ی اصلاحاتی که خود کرده بود توضیح داده است. برخی از رصدهای او که در زیج از آنها نام برده است در سال 267(880) (8) و سپس در سال 287(900) انجام گرفت. در عالم اسلام هیچ کس در رصد ستارگان و تحقیق در حرکات آنها به پای او نمی رسد. گذشته از این، او به احکام نجوم نیز توجه فراوان داشت از این رو در این باره هم چیزهایی نوشت، از جمله آثار او در این زمینه، شرح او بر کتاب الاربعه ی بطلمیوس است.
او از تبار صابیان و از شهر حران بود. چنانکه در پاسخ خود او به نامه ی جعفر بن مُکتَفی آمده است کار رصد را در سال 264(877) آغاز کرد و تا سال 306 (918) بدان اشتغال داشت وی در زیج خود سال 299(911) را برای مبدأ صورت ثوابت اختیار کرده است(9).
او با بنوزَیّات، از مردم رَقّه، که بدانها ظلمی شده بود (10)، به بغداد رفت و در بازگشت در سال 317(929) در قصر الجِصّ درگذشت(11).
آثار او اینهاست: کتاب الزیج به دو تحریر (12)، کتاب مَطالِع البُروج (13)، کتاب اَقدارُ الاتّصالات که برای ابوالحسن بن فرات [وزیر] نوشته است؛ شرح کتاب الاربعة لبطلمیوس (14).
ظاهراً در میان مورخان غربی چنین شایع بوده که بَتّانی از اشرافزادگان و شاهزاده یا حتی شاه بلاد شام بوده است. به این نکته در آثار مسلمانان کوچکترین اشاره ای نشده است و بنابراین منشأ این بدفهمی را باید در آثار اروپاییان سراغ گرفت. قدیمی ترین مأخذی که نلینو به دست می دهد (15) مجسطی نو (Almagestum novum) اثر ریچیولی است (16) که بَتّانی را «حاکم شام» (dynasta Syriae) نام می دهد. ژ. ف. مونتکلا او را «فرمانروای شام از سوی خلیفه» می داند (17)، ول. لالاند(18) و ژ. ب. دلامبر (19) او را «شاهزاده ی عرب» می خوانند، و این دومی ظاهراً از لالاند پیروی کرده است، زیرا به صراحت می گوید که نسخه ای از زیج بَتّانی در دست داشته که در سال 1645 در بولونیا طبع شده و پیش از وی در تملک لالاند بوده است. گرچه عنوان این چاپ زیج هیچ اشاره ای به اشرافزادگی نویسنده اش ندارد(20).
از آثار بَتّانی فقط یک نکته ی دیگر در مورد زندگی او به دست می آید: در زیج خود (21) می گوید که هنگامی که در انطاکیه می زیسته است در 9 صفر 23/289 ژانویه 901 کسوف و در 4 رمضان، 12/289 اوت 901 خسوفی را رصد کرده است.
شهرت بَتّانی در شرق و غرب به سبب کتاب او در نجوم، یعنی کتاب زیج است. عنوان اصلی این کتاب به احتمال زیاد، همان است که ابن ندیم و ابن قفطی ذکر کرده اند: «کتاب الزیج» یا «الزیج». نویسندگان متأخر غالباً آن را زیج صابی (الزیج الصابی) می خوانند (22). واژه ی زیج از واژه ی پارسی میانه (پهلوی) زیک (فارسی جدید: زیگ) مشتق شده است که در اصل تارقالی یا نخدوزی معنی می داده است. چنانکه نلینو متذکر شده است (23)، این واژه در زبان عربی معنای کلیتر «رساله نجومی» را پیدا کرد و برای خود جدول، همین کلمه جدول (به معنای جویبار) رواج یافت(24).
ظاهراً تألیف تحریر اول از دو تحریری که ابن قفطی ذکر می کند پیش از سال 900/288 پایان یافته بوده است زیرا ثابت بن قره که در همین سال 288(فوریه ی 901) درگذشته، از یکی از فصول آن نام برده است (25). چون نسخه ای که در کتابخانه اسکوریال موجود است(26)، و نیز ترجمه لاتینی افلاطون تیولی، شامل رصد کسوف و خسوفی است که قبلاً ذکر کردیم، که یکی از آنها کمی پس از درگذشت ثابت و دومی شش ماه پس از آن انجام گرفته، نلینو چنین حکم می کند (27) که این دو نسخه از روی تحریر دوم استنساخ (یا ترجمه) شده اند.
بَتّانی در مقدمه ای که بر زیج نوشته (28) می گوید که غلطها و اختلافاتی که در آثار پیشینیان می دیده او را بر آن داشته است که به تألیف این کتاب بپردازد، زیرا بطلمیوس خود به نسلهای آینده امر کرده است که بر پایه رصدهای تازه، نظریات و استنباطات او را اصلاح و تکمیل کنند، همچنانکه وی با آثار اَبَرخَس و دیگران همین کار را کرده است(29). نسخه ی عربی مجسطی که مرجع بَتّانی بوده ظاهراً از سریانی ترجمه شده بوده و چنانکه نلینو در موارد متعدد نشان داده از غلط خالی نبوده است. بَتّانی در نقل قول از مجسطی دقیق بوده و نقل قولهای او را می توان با مجسطی تطبیق کرد.
از مقایسه ی زیج بَتّانی و مجسطی درمی یابیم که بَتّانی به هیچ وجه قصد نوشتن مجسطی جدیدی را نداشته است. برای اثبات این گفته، کافی است که چند تفاوت چشمگیر میان این دو را ذکر کنیم:
ترتیب پنجاه و هفت فصل زیج تابع ملاحظات عملی است نه نظری. مثلاً به خلاف فَرغانی که حدود نیم قرن قبل از بَتّانی کتاب خود را تألیف کرده و نه فصل اول آن را (30)را به مباحثی اختصاص داده که در فصول دوم تا هشتم از مقاله اول مجسطی بررسی شده (کروی بودن افلاک و زمین، دلایل سکون زمین، اندازه و قسمت مسکون زمین، دو حرکت اصلی و غیره)، بَتّانی زیج خود را با مسائل و تعاریف کاملاً عملی، یعنی تقسیم کره ی فلکی به بروج و درجات و دستورهایی برای ضرب و تقسیم کسرهای شصتگانی، آغاز می کند. در فصل سوم، که نظیر بخش یازدهم از مقاله اول مجسطی است، نظریه خود را درباره توابع مثلثاتی می پروراند (دنباله مقاله را ببینید)؛ در فصل چهارم به وصف رصدی که خود کرده و از روی آن تمایل دایره البروج را (به مقدار
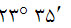) به دست آورده می پردازد، این مقدار بیش از
از مقداری که بطلمیوس به دست آورده کمتر است (
؛ مجسطی، مقاله ی اول، 12) (31) فصول بعدی (دوم تا بیست و ششم)، که تقریباً نظیر بخشهای سیزدهم تا شانزدهم از مقاله اول و تمامی مقاله دوم مجسطی است، حاوی بحث بسیار مستوفایی است درباره بسیاری از مسائل هیأت، که بسیاری از آنها صراحتاً به قصد یافتن پاسخی برای مسائل احکام نجوم طرح شده است.نظریه ی بطلمیوس حرکت خورشید و ماه و سیارات در طول، در فصلهای بیست و هفتم تا سی و یکم آمده است. پس از آن بحثی است درباره تاریخهای معمول و طریق تبدیل آنها به یکدیگر (فصل سی و دوم) (32). این فصل مدخلی است بر شانزده فصل بعدی (فصلهای سی و سوم تا چهل و هشتم) که در این فصول دستورهای جامعی برای استفاده از جدولها درج شده است(فصلهای سی و نهم و چهلم به نظریه اختلاف منظر ماه و فاصله ماه از زمین، که برای محاسبه ی خسوف و کسوف ضروری است، اختصاص دارند.) فصلهای چهل و نهم تا پنجاه و پنجم به بررسی مسائل اصلی احکام نجوم می پردازند. فصل پنجاه و پنجم عنوان عربیش این است «فی معرفة مَطالِعِ البروج فی ما بینَ الاوتادِ الاربعةِ فی الافلاک»(33)، و این همان نامی است که ابن ندیم به یکی از آثار کوچک بَتّانی داده است. شاید این فصل به صورت رساله ی جداگانه ای وجود داشته است و شاید هم ذکر نام آن در فهرست و آثار زندگینامه نویسان دیگر غلطی بیش نباشد.
از دو فصل باقی مانده، فصل پنجاه و ششم به بیان ساختمان شاخصی که ساعتهای نامساوی [مُعوَجَّه] را نشان می داده («رُخامَه» به معنای «قرص مرمری») و فصل پنجاه و هفتم به ساختمان یک نوع ذات الحلق جدید به نام البَیضَة (تخم مرغ) و دو آلت دیگر، که یکی ربع دیواری (در مجسطی، مقاله ی اول، 12:τετάρτημοριον) و دیگری ذاتُ الشُعبَتَین (در مجسطی، مقاله ی پنجم، 12:Ὄργανον παρακτικον) است، اختصاص دارد.
به خلاف روش بطلمیوس در مجسطی، جنبه عملی چنان در زیج بَتّانی غلبه دارد که گاه روشنی بیان را از بین می برد و حتی مطلب را به طور غلط به خواننده می آموزد. این نقیصه در فصل سی و یکم، که حرکت سیارات را بررسی می کند، از همان جا بارزتر است. متن عربی بیش از پنج صفحه نیست که فقط سه صفحه آن به جنبه نظری (یعنی حرکت شناختی) مسئله اختصاص دارد. در اینجا خواننده ای که با شیوه دقیق و گاه دور و دراز بطلمیوس در ارائه براهین آشنا باشد، و نیز خلاصه درخشان فرغانی [فصول] را بشناسد، از ایجاز مُخل و از آن گذشته از بی دقتی و بی کفایتی خلاصه بَتّانی تعجب می کند. به چند خصوصیت که بسیار حیرت آوراند اشاره می کنیم (34). بَتّانی میان نظریه حرکت سه سیاره علوی و ساز و کار پیچیده و دقیقی که بطلمیوس برای نشان دادن حرکت حیرت آور عطارد تعبیه کرده، هیچ تمایزی قابل نشده، و سعی کرده است که فقط با یک شکل که کاملاً ناقص و گمراه کننده است، حرکت هر پنج سیاره را نمایش دهد، و البته موفق نشده است. در این شکل، که در اینجا نقل شده است (شکل 1)، فلک مُعدّل المَسیر (یا مرکز آن: punctum aequans) که مشخصه ی اصلی نظریه بطلمیوسی است نه در شکل نشان داده شده و نه در متن از آن ذکری به میان آمده است. و در نتیجه باید مرکز فلک حامل، M، را همان مرکز حرکت متوسط سیاره دانست. (!).
پی بردن به این اشتباهات کار ساده ای است، و به آسانی می توان نشان داد که اگر این شکل می خواست با نظریه های بطلمیوسی مطابقت داشته باشد به چه صورت در می آمد (شکل 2). شیاپارلی به درخواست نلینو این شکل را فراهم کرده (35)، اما حدس می زند که شکل بَتّانی در اصل درست بوده و خواننده کودنی یا کاتبی آن را تحریف کرده است. اما این حدس مشکل را کلاً رفع نمی کند، زیرا چه کسی جرأت داشته که در متن هم چنان تصرفی کند که نام معدل المسیر بکلی از آن حذف شود؟ و نیز کدام خواننده تازه کاری جسارت ورزیده و نظریه حرکت عطارد را، که نظریه بطلمیوس بدون آن شیر بی یال و دم و اشکمی می شود، حذف کرده است؟ چون متن و شکل نسخه ی خطی کتابخانه اسکوریال و ترجمه افلاطون تیولی (36) هر دو غلط است، پس تحریفی که شیاپارلی مدعی آن است دست کم در قرن یازدهم یعنی در زمان حیات منجم بزرگ مسلمان اسپانیایی، زَرقالی، یا اسلاف نامدار او، رخ داده است. به نظر من اصلاً احتمال ندارد که تحریف عمدی یکی از مهمترین فصول زیج بَتّانی از چشم اینان پوشیده مانده باشد و سعی نکرده باشند که نسخه های تحریف شده را اصلاح کنند و متن اصلی را سرجایش بگذارند. بنابراین من ترجیح می دهم که این امر را ناشی از بی توجهی خود بَتّانی بدانم نه از چیز دیگری، زیرا هیچ حدس دیگری با واقعیات سازگار نیست. مثالهایی از این نوع را می توان از آثار منجمان بزرگتر هم آورد؛ منظورم خطای فاحشی است که بیرونی مرتکب شده (هر چند عواقب آن به این اندازه وخیم نیست) ومن قبلاً در مقاله ای آن را شرح داده ام (37)، ناگفته پیداست که اطلاعات واقعی بَتّانی بسیار بیش از این بوده؛ و برای اثبات این گفته کافی است به جدولهای او از حرکت سیارات، که بسیار مکمل تر از جدولهای بطلمیوس است، توجه کنیم. ترتیب دادن این جدولها بدون آشنایی کامل با نظام بطلمیوسی و همه ریزه کاریهای آن امکان پذیر نبوده است.
هر چند بَتّانی نسبت به حرکت شناخت بطلمیوسی کلاً نظر انتقادی ندارد، چنانکه از کتابش بر می آید در مورد نتایج عملی ای که بطلمیوس به دست آورده نظر شکاکانه ای دارد، و این شک او بجاست، و از این رو با تکیه بر رصدهای خود خطاهای بطلمیوس را تلویحاً یا تصریحاً اصلاح می کند. این اصلاحات هم به پارامترهای اصلی حرکت سیارات مربوط می شود و هم به نتایج اشتباه آمیزی که بطلمیوسی از رصدهای ناقص یا غلط به دست آورده بوده است، مانند ثابت بودن تمایل دایره البروج یا ثابت بودن اوج خورشید.
توجه مسلمانان به مسئله ثابت نبودن تمایل دایره البروج آنقدر زود آغاز شد که مایه شگفتی است، بخصوص که این پدیده، چون در حدود
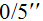در سال است، هیچ کاربرد عملی ندارد. به گفته ابن یونس (وفات1099/399) (38) نخستین اندازه گیری تمایل دایره البروج پس از بطلمیوس اندکی پس از سال 776/160 انجام گرفت و نتیجه ای که از آن به دست آمد
بود که
از مقدار واقعی کمتر است (39). پس از آن او به ذکر چند مقدار دیگر می پردازد که در دوران خلافت مأمون (830/215) به دست آمده است و همه در حدود 
است. بنابراین تعیین تمایل دایره البروج توسط بَتّانی کار خارق العاده ای نبوده، ولی اهمیت آن در این است که او روش به دست آوردن این مقدار
را که کاملاً با مقدار امروزی تطابق دارد، شرح می دهد.بَتّانی در فصل بیست و هشتم زیج به شرح رصد طول فصول که انجام داده می پردازد و از روی آن با استفاده از روش اَبَرخَس، که در قسمت چهارم از مقاله سوم مجسطی شرح داده شده، استنباط می کند که اوج خورشید و مقدار خروج از مرکز آن از دوران باستان تا زمان او تغییر کرده است: اوج خورشید از مقدار
-که ابرخس تعیین کرده و بطلمیوس مدعی شده که تغییر نمی کند- به مقدار 
رسیده و خروج از مرکز خورشید از
کاهش یافته است(
شعاع دایره).بَتّانی، با آنکه خلاف این امر را مدعی است، نخستین کسی نیست که پس از بطلمیوس این مقادیر را تعیین کرده است. بگفته ی بیرونی، (40)، که از شرح ابوجعفر خازن (وفات، حدود 961/350) بر مجسطی نقل قول می کند، نخستین رصد برای تعیین مقدار اوج خورشید، با استفاده از روش جدید «چهار فصل» که به همین منظور درست شده بود (41)، در سال 830/215 در محله شماسیه ی بغداد انجام گرفت؛ اما با وجود برتری روش آن بر روش پیشین نتیجه ای که به دست آمد بسیار بد و حداقل
کمتر از مقدار واقعی بود. یک سال بعد، ثابت بن قره (یا بنوموسی) با استفاده از همان روش قدیمی بطلمیوس مقدار
درجه را که بسیار عالی است به دست آورد (42). ثابت (یا بنوموسی) با مقایسه این مقدار یا مقدار ابرخس و با رد نظری که بطلمیوس در تأیید آن آورده بود، دریافت که مقدار حرکت اوج خورشید
در هر 66 سال است؛ و از آنجا که می دید ابرخس همین مقدار را برای تقدیم اعتدالین به دست آورده است، نتیجه گرفت که این دو مقدار لزوماً باید یکی باشند. به عبارت دیگر اوج خورشید هیچ گاه نسبت به ستارگان ثابت تغییر نمی کند. (در فلسفه ی مدرسی اروپا، این نوع استدلال و نتیجه گیری را «اُستُره ی اُکّام» نام داده اند.)مقداری که بَتّانی برای اوج خورشید به دست آورده
() به خوبی مقدار ثابت بن قره (یا بنوموسی) نیست، هر چند تطابق کامل نتیجه ثابت را با مقداری که امروزه از راه فرمول به دست می آید باید تا حدودی تصادفی دانست. فرمول لووریه(1) برای سال 831/216 مقدار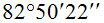
(ثابت بن قره:
و برای سال 884/271 مقدار
(43) (بتّانی، 
) را به دست می دهد. جالب است که مقدار ابرخس (
برای حدود سال 140 ق. م.) نیز با مقدار امروزی که
است بسیار خوب می خواند.پس بَتّانی را به هیچ وجه نمی توان کاشف حرکت اوج خورشید دانست، و نیز او هم مانند ثابت بن قره نمی توانست حکم کند که آیا این حرکت با تقدیم اعتدالین یکی است یا نه. حدود 150 سال گذشت تا ابوریحان بیرونی مبنای نظری تمایز این دو پدیده را به دست داد (44)، اما او هم ناگزیر اعتراف کرده است که با داده هایی که در دست دارد نمی تواند در این مورد حکم قاطعی بکند. نخستین کسی که مقدار حرکت خاص اوج خورشید را به صورت عددی روشن (و بسیار صحیح) به دست داد، زرقالی طُلَیطَلی (نیمه دوم قرن ششم/ دوازدهم) بود که این مقدار را
درجه در 29 سال یولیانی، یا
در سال، تعیین کرد (مقدار امروزی، 
)، اما چون او هم مانند ثابت بن قره حرکت اِقبال و اِدبار را واقعی می دانست، نتوانست از این نتیجه نجومی استفاده کند.مقداری را که بَتّانی برای خروج از مرکز مدار خورشید به دست آورده
و با علامات امروزی برابر است با 0/017326 (مقداری که از راه فرمول برای سال 880/267 به دست می آید، برابر است با 0/16771) در مقام مقایسه با مقداری که بطلمیوس به دست آورده و بسیاری بیش از مقدار واقعی است (0/0208 به جای 0/0175) (45) باید بسیار خوب دانست.از جمله توفیقات مهم بَتّانی یکی اصلاح حرکت متوسط ماه در طول است (46)؛ دیگر اندازه گیری قطر ظاهری خورشید و ماه و تغییرات آنهاست در طول یک سال یا یک ماه حضیضی، که بر اساس آن نتیجه می گیرد که کسوف حلقوی امکانپذیر است (به خلاف نظر بطلمیوس که آن را ناممکن می داند) (47)؛ همچنین روش بدیع و بسیار زیبایی برای محاسبه قدر خسوف وضع کرده است(48).
در مورد مقدار تقدیم اِعتدالَین، او مقداری را که ثابت بن قره به دست آورده (
در هر 66 سال)، و از مقدار بطلمیوس (
در هر صد سال) بسیار بهتر است ولی در حدود 10 درصد بیش از مقدار واقعی (
در هر 72 سال) است، می پذیرد. در نتیجه، طول سال اعتدالی او 
به اندازه ی
از مقدار واقعی زیادتر است.سیاهه ی بَتّانی از ستارگان ثابت (49) (489 ستاره) به هیچ وجه در جامعیت به پای سیاهه بطلمیوس (1022 ستاره) نمی رسد. قَدر ستاره ها و عرض آنها را (احیاناً با اصلاحاتی) از مجسطی برداشته اما بر طول آنها مقدار
می افزاید، که متناظر است با 742 سال فاصله ی زمانی میان مبدأ دو سیاهه (137 ق. م. و 880/267) و حرکت تقدیمی که قبلاً گفتیم، یعنی
در هر شصت و شش سال.هر چند بَتّانی از مجسطی فراوان نقل قول می کند، فقط یک بار (در پایان فصل پنجاه و پنجم) از کتاب الاربعة ذکری به میان می آورد. نمی دانیم که آیا بَتّانی کتاب جغرافیای بطلمیوس را می شناخته و از آن استفاده می کرده یا نه(50). از کتاب فرضهای سیاره ای بطلمیوس (که نویسندگان بعدی آن را کتاب الاِقتِصاص یا کتاب المَنشورات می خواندند) (51) در فصل پنجاهم که مختص فاصله سیارات است استفاده شده است، اما بَتّانی نظریه افلاک مقارن را، که محاسبه ی فواصل بر اساس آن صورت می گیرد، به «دانشمندان پس از بطلمیوس» نسبت می دهد. چون فرغانی در این مورد از کسی نام نمی برد (52)، محتمل به نظر می رسد که اشاره بَتّانی به «دانشمندان پس از بطلمیوس» منعکس کننده عبارتی از هوپوتوپوسیس پروکلوس (53) باشد که در آن هم نام بطلمیوس نیامده است. و هنگامی معلوم شد که مؤلف کتاب الاِقتِصاص همان بطلمیوس است که این کتاب، اندکی پیش از روزگار بیرونی، به عربی ترجمه شد.
بَتّانی از میان سایر آثار نجومی دوران باستان فقط از جدولهای دستی تئون اسکندرانی نام می برد. در بخشی از فصل پنجم که به مسائل جغرافیایی می پردازد (54) بی آنکه مقصود خود را معلوم کند از «قدما» نام می برد. نلینو نشان داده است (55) که در این مورد منظور او منابع یونانی سریانی است.
هر چند چنانکه قبلاً ثابت کردیم میان بَتّانی و بنوموسی و ثابت بن قره بسا چیزهایی مشترک هست، وی در زیج خود به هیچ وجه از اسلاف مسلمانش نام نمی برد. از لحاظ اصطلاحات، او از استعمال واژه های بیگانه (فارسی یا هندی) که در آثار اسلامیان پیش از او یافت می شود، خودداری می کند، مانند واژه اوج برای دورترین نقطه فلک خارج از مرکز بَتّانی به جای آن عبارت دور و دراز «البُعد الاَبعَد من الفلک الخارج المرکز» را به کار می برد جَیب، برای سینوس (بَتّانی: «وتر مُنصِّف»یا «وتر») بُهت، برای حرکت (نامساوی) سیاره در طول روز (بَتّانی از این مفهوم استفاده نمی کند)؛ جَوزَهَر، برای عقده ی صاعِد (بَتّانی: «رأس»)، هَیلاج، به معنی «دالّه» در احکام نجوم (به یونانی:
، بَتّانی : «دلیل»)؛ و غیره (56). اما یقیناً خودداری او از استعمال اصطلاحات بیگانه ناشی از «سره نویسی» نیست، بلکه دلیلش این است که در ترجمه های مجسطی که او در دست داشته این الفاظ وجود نداشته اند، به همین دلیل است که او در مواردی عین واژه های یونانی را به صورت نامناسبی نقل می کند، مانند اَفیجیون که همان
(«اوج») و فِریجیون که همان
(«حضیض») است.بَتّانی به پیروی از اسلاف مسلمان خود که مفهوم هندی سینوس (مأخوذ از سِند هِند) را با مفهوم کهن یونانی وتر آمیخته بودند، از سینوس (جیب) به جای وتر [روبروی دو برابر زاویه] استفاده می کند. گذشته از سینوس، از کسینوس («وتر مابیقی لِتَمام... الی تِسعین» یعنی «سینوس متمم زاویه... تا 90» و سینوس معکوس (R-Cos)، که آن را «وتر راجع» می نامد) هم استفاده می کند. مؤلفان بعدی خط مثلثاتی اخیر را دو برابر جَیب مُستوی (سینوس معمولی) یا سَهم، که واژه ی لاتینی قرون وسطایی Sagitta از آن مشتق شده، یا جَیب معکوس نام داده اند. در فرمولهای بَتّانی از تانژانت و کتانژانت خبری نیست، و از این رو فرمول های او مانند بطلمیوس چه با دشوار و دیریاب می شوند. وی از این دو خط در شناخت شاخص استفاده می کند که در این مورد به شاخص دوازده بخشی مربوط می شوند، چنانکه در سند هند هم چنین است. وی برای کتانژانت اصطلاح ظِلّ مَبسوط (لاتینی: umbra extensa»؛ دیگران اصطلاح ظِلّ مستوی را به کار برده اند، لاتینی: umbera recta) و برای تانژانت اصطلاح ظِلّ مُنتَصَب (لاتینی: umbra erecta) را به کار می برد (57)، بَتّانی با استفاده از نکاتی که مبتنی بر اصل تصویر قائم است، روشهای نو و زیبایی در حل مسائل مثلثات کروی ابداع کرده است. در اروپا این اصل را رِگیومونتانوس (1436-1476) اخذ و تکمیل کرد.
مبدأ تاریخ اصلی بَتّانی (تاریخ ذوالقرنین= تاریخ اسکندر مقدونی) شنبه اول سپتامبر 312 ق. م. است که سی روز جلوتر از تاریخ ذوالقرنینی است که دیگر مؤلفان مسلمان به کار برده اند، و آن دوشنبه اول اکتبر 312 ق. م. است. این تاریخ با سال یولیانی آمیخته شده است. وی برای ماهها نامهای سریانی را به کار می برد: اَیلول (سپتامبر)، تِشرین اول، تِشرین ثانی، کانون اول، کانون ثانی، سَباط (شباط؟)، آذر، نیسان، اَیّار، حَزیران، تَمّوز، آب. مبدأ تاریخ قِبطی (تاریخ القبط) جمعه بیست و نهم اوت 25 ق. م. است، اما دیگر مؤلفان مسلمان وقتی این تاریخ را به کار می برند منظورشان یکی از این سه تاریخ است: تاریخ بختنصر (اول توث=26 فوریه 747 ق. م. ) تاریخ فیلیپ (12 نوامبر 324 ق. م. از این تاریخ در مجسطی به عنوان «تاریخ مرگ اسکندر» یاد شده است)، و تاریخ دقلطیانوس (29 اوت 284 ق. م.، که تاریخ الشهدا هم خوانده شده است) (58).
ترجمه لاتینی زیج بَتّانی اثر یک نفر انگلیسی به نام روبرت رتینایی(Robertus Retinensis، یا R. Ketenensis یا Castrensis یا Cestrensis؛ به اعتقاد نلینو نسبت صحیح او Cataneus است (59))، که دوران شکوفاییش در اواسط قرن دوازدهم میلادی بوده، باقی نمانده است. تنها ترجمه لاتینی بازمانده، ترجمه افلاطون تیولی است که دوران شکوفاییش در بارسلونا در نیمه اول قرن دوازدهم میلادی بوده است، این ترجمه دوبار چاپ شده است. چاپ اول (نورمبرگ، 1537) عنوانش این است:
Rudimenta astronomica Alfragrani[sic] (60). Item Albategnius peritissimus de motu stellarum ex observationibus tum propriis tum Ptolemaei, omnia cum demonstraitionibus geometricis et additionibus Ioannis de Regiomonte;
عنوان چاپ دوم، که بدون فصول فرغانی چاپ شده (بولونا، 1645)، این است:
Mahometis Albatenii de scientia stellarum liber cum aliquot additionbius Ioannis Regiomontani. Ex Bibliotheca Vaticana transcriptus(61).
نسخه ای از ترجمه اسپانیایی زیج که به دستور شاه آلفونسوال سایبو(1252-1284) انجام گرفته در کتابخانه زرادخانه (Bibliotheque de I'Arsenal) پاریس موجود است(62).
هر چند زیج بَتّانی ظاهراً به عبری ترجمه نشده، اما تأثیر عظیمی بر علم یهودی داشته است. صاحب الشُّرطه (وفات: حدود 1136/530) و ابراهیم بن عِزرا (1167-1090 حدود 483/562) از آن نام برده و آن را ستوده اند. ابن میمون (530-601/1135-1204) در مقاله ی هشتم از کتاب میشناتوره (تفسیر میشنا)، که عنوانش «هلوک کِدّوش ها حودِش»(63) است، بی آنکه نامی از بَتّانی ببرد از او تبعیت کرده است. در فصلهای دوازدهم تا چهاردهم پارامترهایی که به کار برده (حرکت متوسط خورشید و ماه در طول، حرکت اختلافی متوسط ماه، تعدیل خورشید) همان مقادیر بَتّانی را دارند، با این تفاوت که در مورد مقادیر تعدیل خورشید، کسرهای کوچکتر از دقیقه را ذکر نکرده است (64). روشی هم که ابن میمون برای تعیین حدود رؤیت هلال ماه توصیه کرده، دقیقاً از روش زیبای بَتّانی پیروی می کند.
بَتّانی نزد منجمان و مورخان مسلمان مقام شامخی دارد. بیرونی کبیر کتابی دارد به نام جلاء الاذهان فی زیج البَتّانی (65) و ابن خلدون (1406-1332/808-732) کتاب او را از جمله بهترین کتابهای نجوم در اسلام می داند (66).
در نوشته های بوزنطی نام بَتّانی به صورت «اُپَتَنِس»
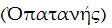ذکر شده، اما ظاهراً کتاب او به یونانی ترجمه نشده است. بسیاری از نویسندگان لاتینی قرون وسطی زیج را می شناخته اند یا دست کم نام مؤلف آن را ذکر کرده اند. از آن جمله است هنری بیت (1246 -حدود 1310) که در تألیف Magistralis composito Astrolabii anno scripta1274 از زیج استفاده ی فراوان کرده و در اغلب موارد حق مؤلف آن را هم ادا کرده است؛ گرارد سابیونتایی؛ آلبرت کبیر؛ لِوی بن گِرشون (در ترجمه ی لاتینی نجوم خود) (67)؛ و مهمتر از همه رگیومونتانوس، که توجه فراوان او به این کتاب از حواشی بسیاری که به خط خود بر ترجمه افلاطون تیولی نوشته و ضمیمه ی چاپهای نورمبرگ و بولونیا به طبع رسیده، نمایان است. استاد اوگئورگ پویِرباخ (1461-1423) در کتاب Theoricae planetarum، که توسط رگیومونتانوس ویرایش و چاپ شده(68)، فقط در یک مورد از بَتّانی نام می برد (برگ 18، پشت) (69)، و در آنجا می گوید که بَتّانی ("Albategni") به خلاف کسانی که از نظریه ی اقبال و ادبار دفاع می کردند معتقد بود که ستارگان در هر شصت و شش سال و چهار ماه 1° حرکت می کنند(70) و این حرکت همیشه از غرب به شرق است. چون منجمان اسلامی، و نیز متن و ترجمه کتاب بَتّانی که بازمانده، همه تصریح دارند که بَتّانی معتقد به
حرکت در هر شصت و شش سال بوده (71)، معلوم نیست که این مقدار غلط، که بی شک ناشی از اشتباه نساخ نیست، از کجا به کتاب پویرباخ راه یافته است. پویرباخ حرکت شناخت سیارات را طبق نظر بطلمیوس استادانه عرضه کرده، و با توجه به آنچه درباره فصل سی و یکم از کتاب بَتّانی گفتیم(72)، بی شک الگوی او این فصل معیوب از زیج بَتّانی نبوده است؛ اما تأثیر فرغانی بر او در موارد بسیاری محسوس است.تأثیر بَتّانی بر کوپرنیکوس چیز آشکاری است. وی درموارد بسیار و بخصوص -مثل پویرباخ- در فصولی که به مسائل حرکت خورشید و تقدیم اعتدالین اختصاص دارد، از بَتّانی نقل قول می کند (73). در نوشته های تیکوبراهه و مجسطی نو ج. ب. ریچیولی اشارات بیشتری به او شده است (74). گذشته از این کپلر و نیز گالیله در نوشته های نخستینش توجهی به رصد های بَتّانی نشان می دهند.
از لحاظ تاریخ علم باید از دو نفر نام برد، گرچه ارج این دو یکسان نیست. در 1819، دلامبر تاریخ نجوم در قرون وسطی را منتشر کرد (75). در فصل دوم کتاب، وی پنجاه و سه صفحه را به تجزیه و تحلیل زیج بر اساس چاپ بولونیای ترجمه افلاطون تیولی اختصاص می دهد. این فصل حتی برای خواننده امروزی هم جالب است، گرچه نوعی غرور، که در همه آثار دلامبر مشهود است، گاهی اسباب شگفتی می شود؛ زیرا برای ما جالبتر آن است که بدانیم محیط تاریخی که کتاب بَتّانی در آن تکوین یافته چگونه بوده، تا اینکه پی ببریم که فلان یا بهمان مسئله راه حل سرراستتری هم دارد. اما دلامبر توانایی این کار را نداشت، زیرا حتی اگر عربی را هم خوب می دانست (که هیچ نمی دانست) تنها نسخه عربی این کتاب را در دسترس نداشت، از این رو ناچار به ترجمه افلاطون تیولی استناد می کند و اشتباهات و بدفهمیهای آن وی را در موارد بسیار به بیراهه می کشاند.
هشتاد سال پس از دلامبر، خاورشناس جوان ایتالیایی، کرلو آلفونسو نلینو، متن کامل عربی زیج بَتّانی را منتشر کرد که نمونه ای است در کار تحقیق (76). دو جلد بعدی، که حاوی ترجمه لاتینی زیج و حواشی بسیار مبسوط و عالمانه است، ظرف هشت سال بعد منتشر شد. در زمان ما، که افراط در ستایش بسیار معمول است، نمی توان لفظی یافت که شایسته کار نلینو باشد. نثر عربی بَتّانی، که در نظر اول ساده و سرراست می نماید اما در بسیاری از موارد در واقع دشوار و حتی مبهم است، چنان به لاتینی روشن و روان ترجمه شده که در خور هر گونه ستایش است. هنگام مطالعه این کتاب، که شاهکار نلینو است، در می یابیم که او از روی هوس و تفنن به ترجمه به لاتینی نپرداخته است. از لحاظ فنی، ترجمه نلینو، برهان آشنایی عمیق او با مسائل ریاضی و نجوم زیج و نیز حوادث تاریخی ای است که این کتاب بر زمینه آن ها تدوین شده است. ترجمه سوم لاتینی زیج، که هشت قرن پس از دو ترجمه دیگر صورت گرفته، تا ابد یکی از شاهکارهای تاریخ علم خواهد بود.
تا این اواخر گمان می رفت که سه کتاب کوچک بَتّانی (که موضوع هر سه احکام نجوم است) و نامشان در فهرست ابن ندیم و تاریخ الحکمای قفطی آمده (77)، از بین رفته است؛ زیرا از یک طرف اصالت نسخه ای که در برلین است مشکوک بود (78) و از طرف دیگر تنها نسخه بازمانده که صراحتاً عنوان «تفسیر کتاب الاربعه بطلمیوس» دارد و هنوز هم نامش در فهرست کازیری وجوددارد (79)، به شهادت هـ. درنبورگ در 1884 (80) و نلینو در 1894 و کشیش پدرو بلانکوسوتو در 1901 (81)، دیگر در کتابخانه اسکوریال یافت نمی شود. اما خوشبختانه این نسخه گمشده ظاهراً از نو پیدا شده است. در فهرست جدید رنو (82) این نسخه به شماره 969، 2 (نه شماره ی 966 که در فهرست کازیری هست) تحت عنوان کتاب اربع مقالات فی احکام علم النجوم ثبت شده است. تاریخ دستنوشت 1533/939 است و کتاب شصت برگ دارد. البته کلمه «شرح» درعنوان کتاب وجود ندارد، اما رنو و کازیری هر دو آن را «شرح کتاب الاربعه ی بطلمیوس» دانسته اند. پژوهش در یکی بودن نسخه برلین و نسخه اسکوریال به تحقیق ویژه ای نیاز دارد. چون در نسخه اسکوریال جدولهایی هست (که در متن اصلی یونانی نیست) معلوم می شود که در این نسخه قواعد و توصیه هایی برای کاربرد آنها وجود دارد، و از این نظر شاید بتوان آن را «شرح» دانست.
در این مورد (83) نلینو یادآور می شود که علی بن رضوان مصری (لاتینی: Haly Heben Rodan؛وفات: 1061/453) گفته است که هیچ گاه شرحی از کتاب الاربعه ندیده است؛ ولی ابوالحسن علی بن ابی الرِّجال (لاتینی: Albohazen Haly filius Abenragel شکوفایی: حدود 1050/442) بَتّانی را از جمله کسانی می شمارد که، مانند بطلمیوس، برای پیشگوییهای احکامی بر اساس کسوفهایی که در سالهای اقتران سیارات رخ می دهند، اهمیت زیادی قائلند. ظاهراً نلینو معتقد است که منظور ابن ابی الرجال قسمت ششم از مقاله ی دوم از کتاب الاربعة (84) است که به همین موضوع اختصاص دارد. اما واقع امر چنین نیست. در کتابخانه ی اسماعیل سائب در آنکارا نسخه ای وجود دارد (شماره 1 /119) که شامل سه کتاب مختلف است و عنوان دومی (برگهای 27 پشت 42 رو) چنین است: کتاب [محمد بن] جابربن سنان الحرانی البطانی فی دلائل القرانات و الکسوفات (85). بی شک قول ابن ابی الرجال به همین کتاب، که نامش در هیچ یک از فهرستهای بزرگ اسلامی نیامده، مربوط می شود. من که فقط تورقی در نسخه زیراکس این کتاب در پژوهشکده ی تاریخ علم دانشگاه فرانکفورت کرده ام، دلیلی برای تردید در اصالت آن نمی بینم.
در نسخه ی خطی دیگری که عنوانش تجرید اصول ترکیب الجیوب (86) است، نام بَتّانی دیده می شود. چون بَتّانی دست کم در زیج، از استعمال واژه ی جیب(جمعش، جیوب) برای سینوس خودداری می کند (87)، می توان این نسخه را ساختگی دانست.
سیاهه ی تعدادی دیگر از آثار که انتسابشان به بَتّانی قطعاً نادرست است، و فقط نسخه ی لاتینی آنها وجود دارد، (همراه بحثهای مستوفا) در کتاب نلینو آمده است(88).
حواشی:
1. کتاب الفهرست (تاریخ تألیف حدود 987/377). ویراسته ی گ. فلوگل (لایپزیگ، 1872-1871)، 1، 279 همچنین ر. ک.
C. A. Nallino, Al-Battani sive Albatenii Opus astronomicum, ad fidem codicis escurialensis arabice deitum, latine versum, adnotationibus instructum, I(Milan,1903) viii ff.
این شاهکار، که از این پس آن را نلینو می نامیم (جلد دوم، 1907، جلد سوم، 1899) همیشه منبع اصلی نجوم اسلامی عموماً و بَتّانی خصوصاً خواهد بود.
2. ر. ک.
B. Carra de Vaux, "al-Sabia, " in Encyclopedia of Islam, 1st ed. , IV;
و برای اطلاعات جامع (هر چند گاهی قدیمی). ر. ک.
D. Chwolsohn , Die Scabier und der Ssabismus , Vols I/II(St. Petersburg, 1856).
3. Die Ssabier , I, 611.
4. نلینو، xiii, II.
5. فهرست، ص 285.
6. همان، ص 280.
7. ویراسته ی. لیپرت (لایپزیگ، 1903)، ص280. ابن قفطی مؤلف تاریخ الحکما در سال 1284/646 درگذشت. فصلی که درباره بَتّانی نوشته (و من از آن پیروی کرده ام) به گفته ی خودش بر قول صاعِد اندلسی مبتنی است و در آن اطلاعاتی هست که در فهرست نیست.
8. به دلیل خطای ناسخان، در فهرست و ابن قفطی 269 آمده است.
9. به جای 911/299 (که خطای ناسخ است) بخوانید 880/267. تاریخ واقعی سیاهه همین 880/267 است.
10. ظاهراً معنایش این است که از آنها مالیات بیمورد خواسته بودند. معلوم نیست که آیا بَتّانی هم جزء «آنها» است یا نه. ر. ک. نلینو، viii,I. در مورد بنوالزیات، نلینو(همان، xviii به بعد) معتقد است که بی شک ایشان اعقاب شاعر و وزیر معروف عبدالملک بن اَبان الزَّیات بوده اند (که در سال 847/233 به امر متوکل کشته شد). ابن وحشیه کتاب الفلاحة النَبَطیّة خود را که مدعی بود از سریانی ترجمه کرده، به یکی از اسلاف این عبدالملک به نام ابوطالب احمد الزیات املا کرد.
11. in Ibn Khallikan's (d. 681/1282) biographical dictionary (Eng. trans. by Mac Guckin de Slane, Paris-London, 1843-1871, IV, 317-320;
در اصل عربی کتاب وفیات الاعیان
Ibn Chalikan, Vita illustrium virorum, F. Wustenfeld, Gottingen, 1835-1842,no. 719.
[به نقل از نلینو، I، ix، حاشیه 6]، نام محل مرگ بَتّانی «قصر الحَضر» آمده است. نلینو ثابت کرده (نلینو، ص xviii) که قصر الجِصّ درست است (و قصر الحضر تصحیف آن است).
12. ابن ندیم و ابن قفطی می افزایند: «تحریر اول و تحریر دوم، که تحریر دوم بهتر است».
13. ابن ندیم عبارت «فی مابین اربع الفلک» (در فضای بین چهار نقطه اصلی فلک) را اضافه دارد. در این کتاب مسئله ی احکامی یافتن جهت «تَسییرِ دَلیل» به صورت ریاضی حل شده است.
14. نامش در فهرست ابن ندیم نیامده.
15. نلینو، I. xviii حاشیه 1.
16. Bologna, 1651, II,xxix.
17. Histoire des mathematiques, new ed. (Paris,1797-1800) , I,368.
18. Astronomie, 3rd ed. (Paris, 1792) , I,123.
19. Histoire der l'astronomie du money age(Paris, 1819; repr. New York-London, 1965) , pp. 4,10.
20. در عنوان این کتاب نام نویسنده به صورت
"Mahometus, filius Geber, filius Grueni, qui vocatur Albategni. "
(مَحُمِتوس (محمد)، فرزند گِبِر (جابر) فرزند کروئِنوس، معروف به البتگنی) آمده است. نام عجیب کروئنوس بی گمان تصحیف «سنان» است که احیاناً به صورت «کینسوس» تلفظ شده است.
21. فصل سی ام، نلینو، I، 65.
22. مثلاً ابن خلکان (1282-1211/681-608) و حاجی خلیفه (1017-1067/ 1609-1657) ر. ک.
Haji Khalifae Lexicon bibliographicum et edcyclopaedicum, ed. and trans. , with commentary, by G. Flugel(Leipzig-London,1835-1858) , III, 564, no. 6946.
23. نلینو، I، xxxi، حاشیه 3.
24. در یونانی بوزنطی، این واژه ξῆσι و مترادف با Συντάξεις است. ر. ک. نلینو، xxxi، حاشیه 5.
25. ر. ک. فصل پنجاه و هفتم که درباره ی نظریه اِقبال و اِدبار بحث می کند. بَتّانی منکر این نظریه است و ثابت قائل بدان. ثابت در نامه خود به اسحاق بن حنین به بَتّانی اشاره کرده این نامه را ابن یونس حفظ کرده است. ر. ک. نلینو، 298.
26. در اصل شماره ی آن 903 بوده:
(M. Casiri, Bibliotehca arabico-hispanica Escurialensis, Madrid, 1760, I, 342-343),
ولی اکنون 908 است. باور کردنش دشوار است، ولی از این کتاب که از مهمترین کتابهای قرون وسطاست، فقط یک نسخه به زبان اصلی عربی باقی مانده است.
27. نلینو، I، xxxiii.
28. فصل یکم، نلینو، I، 5
29. Almagest,III, 1(German trans. by Karl Manituis, Des Claudius Ptolemaus Handbuch der Astronomie, Leipzig, 1912,p. 141).
عبارت این کتاب کمی فرق می کند و هیچ گونه «امر» صریحی در برندارد.
30. جز فصل یکم، که راجع به تاریخهای مختلف و تبدیل آنها به یکدیگر است و عملاً معادل فصل سی و دوم بَتّانی است. رک.
Golius 'ed. dnd Latin trans. : Muhammedis fil. Ketiri Ferganesis, qui vulgo Alfraganus dicitur, Elementa astronomica (Amsterdam,1669).
31. ر. ک.
W. Hartner, " The Obliquity of the Ecliptic According to the Hou-Han Shu and Ptolemy, " in Sliver Jubliee Volume of the Zinbun-Kagaku-Kenkyusyo (Kyoto,1954) , pp. 177-183; repr. in Hartner's Oriens-Occidens (Hildesheim,1968) , pp. 208-214.
32. ر. ک یادداشت 30.
33. ر. ک. ص 508 و یادداشت 13.
34. ر. ک شکل و متن مربوط بدان در نلینو، III، 96 به بعد (به عربی) و نلینو I، 64 به بعد (به لاتینی) که شکل 1 را ما از آن گرفته ایم.
35. نلینو، I، 237 به بعد. شکل 2 را ما از روی شکل شیاپارلی رسم کرده ایم.
36. نلینو، I, Ixvii می گوید که نسخه ای عربی که ترجمه افلاطون تیولی از روی آن انجام گرفته و نسخه ی اسکوریال (که طبق نظر نلینو در حدود 1100/493) نوشته شده) هر دو مأخذ واحدی دارند.
37. "Mediaeval Views on Cosmic Dimensions and Ptolemy's Kitab al-Manshurat," in Melanges Alexandre Koyre, I(Paris, 1964) , 254-282; repr. in W. Hartner, Oriens Occidens(Hildesheim, 1968) , pp. 319-348.
38. Bibliotheque Nationale, MS Ar. 2405, p. 222(cited after O. A. 1,157).
39. برای تحقیق دقیق این مسئله و مقایسه آن با فرمولهای امروزی (نیوکومب، دوسیتر) باید تأثیر شکست نور و اختلاف منظر خورشید را هم در نظر گرفت. با این کار این مقدار در حدود 40 کاهش می یابد، که البته در اینجا اهمیتی ندارد(ر. ک. پانوشت شماره 31).
40. قانون مسعودی، شش، فصلهای 7 و 8 (القانون المسعودی، چاپ دائره المعارف عثمانیه، 2(حیدرآباد دکن، 1955/1374)، صص650-685). مقایسه کنید با
W. Hartner and M. Scharmm, " Al-Biruni and the Theory of the Solar Apogee: An Example of Originality in Arabic Science, " in A. C. Crombie, ed. , Scientific Change (London, 1963) , pp. 206-218.
41. یعنی رصد عبور خورشید از نقاط °15 برج ثور، °15 اسد، °15 عقرب، و °15 دلو.
42. به موجب کتاب سَنه الشمس بالاَرصاد، نسخه خطی لندن، ایندیا آفیس، شماره ی 734، برگهای 13، 11، 6r به بعد.
43. شیاپارلی (O. A. I, 215) برای سال 884/271 مقدار 83°5051را می دهد، که اشتباه است.
44. Hartner and Schramm(n. 40) ,pp. 216-218.
45. مقایسه کنید با O. A. I, 213f برای مقایسه مقادیر قدیم و جدید (خروج از مرکز بیضی)، البته باید مقدار قدیمی را نصف کرد:
2^p 445/60=0/034653=20/017326
46. مقایسه کنید با A. O. I, 225f.
47. مقایسه کنید با همان، 58، 236. او یا از این نکته غافل است و یا به روی خود نمی آورد که مقادیری که برای قطر ظاهری ماه در اوج (d_1=29/5) و در حضیض (d_2=35/3) رصد کرده به نسبت 5: 6 اند. طبق نظریه ی بطلمیوس این مقادیر باید به نسبت 17: 33، یا تقریباً 1: 2؛ باشند.
48. مقایسه کنید با همان. 99f.
49. متن عربی،
O. A. III, 245-274; Latin, O. A. ,II, 144-177.
50. Cf. O. A. , I, xli and 20(end of ch. 4).
51. W. Hartner, "Mediaeval Views on Cosmic Dimensions" (n. 39) , and B. R. Goldstein, " The Arabic Version of Ptolemy's Planteray Hypotheses, " in Transactions of the American Philosophical Society , n. s. 57, pt. 4(1967).
52. Ch. 21, pp. 80-82; see n. 32.
53. Procli Diadochi Hypotyposis astronomicarum positionum , ed and trans. into German by K. Manitius (Leipzig, 1909) , ch. 7, 19(p. 220).
چنانکه من در «نظریات قرون وسطاییان... » (ر. ک. پانوشت شماره 37) نشان داده ام، دیگر شکی نیست که مفهوم افلاک مقارن را بطلمیوس دریافته بوده است. دلیل نهایی بر درستی نظر مرا گلدشتین به دست داده است (ر. ک. پانوشت شماره 51)، وی دریافته است که بخشی که در متن هایبرگ Claudii Ptolemae opera, II, Opera astronmica minora,) در آخر مقاله ی اول افتادگی دارد در نسخه های موجود عربی و عبری کتاب الاقتصاص موجود است. پارامترها و نسبتهایش هم همان است که من در مقاله ام ذکر کرده ام.
54. O. A. , I,17-19.
55. Ibid. , 165-177.
56. Cf. ibid. , xlii f.
57. در پشت اسطرلابها معمولاً عبارت ظل مبسوط برای سایه ای که شاخص قائم روی صفحه افقی می اندازد و ظل معکوس (گاهی ظل مَنکوس) برای سایه ای که شاخص افقی روی صفحه قائم می اندازد به کار رفته است.
58. برای کسب اطلاع بیشتر، رک. 246-242, I,. A. O.
59. ر. ک. xlix f, I,. A. O. شک نیست که منظور از این نام، روبرت اهل چِستِر است که دوست هِرمانوس دالماتا بوده است. وی نخستین کسی است که (در 1143) قرآن را به لاتینی ترجمه کرد و از نخستین مترجمان کتاب الجبر والمقابله مجمد بن موسی خوارزمی به زبان لاتینی است. ر. ک. L. C. Karpinski, "Robert of Chester's translation of al-Khowarizmi, " in Bibliotheca mathematica, 11(1911) , 125-131.
روبرتوس رتینن زیس با روبرتوس آنگلیکوس یکی نیست. این دومی درقرن سیزدهم میلادی می زیسته است.
60. به ویرایش دیگر فصول فرغانی که در پانوشت شماره 30 به آن ارجاع دادیم مراجعه کنید. تبویب کتاب در این دو ویرایش یکسان نیست.
61. در مورد ترجمه ی لاتینی و ویرایش نلینو، ر. ک. ص 268.
62. وصف آن در مرجع زیر آمده است:
Rico y Sinobas in Libros del saber de astronomia del Rey D. Alfonso X de Castilla, V, pt. 1(Madrid, 1867) , 19f.
63. Cf. O. A. , I, xxxiv; and S. Gandz trans. , " The Code of Maimonides, Book III, Treatis 8, Sanctification of the New Moon; With Supplementation and an Introduction by J. Obermann and an Astronomical Commentary by Otto Neugebauer , " in J. Obermann, ed. , Yale Judaica Series, XI(New Haven, 1956) , 47-56.
64. O. A. , II, 20, 22, 75 and 78 ff.
توجه داشته باشید که برای حرکت متوسط ماه مقادیری که در جداول صفحات 22 و 75 برای شناسه های 〖10〗^d 〖و9〗^dداده شده، به مقدار 1و2 تفاوت دارند. مقادیر صفحه 75 درست اند:
9^d,8°5215 ;〖10〗^d ,9°5123 .
65. جلاء الاذهان فی زیج البَتّانی، طبق فهرستی که خود بیرونی از آثارش ترتیب داده و در کتاب زیر چاپ شده است:
E. Sachau , ed., Chronologie orientalischer Volker von Alberuni (Leipzig, 1878) , p. xxxxvi.
66. Cf. de Slane , Les prolegomenes d'Ibn Khaldun(Paris, 1863-1868) , III, 148; cf. F. Rosenthal, trans. , Ibn Khaldun, The Muqaddimah, III(New York, 1958) , 136.
67. Cod. Vat. Lat. 3098(cited after O. A. , I, xxxvi).
68. نورمبرگ، حدود 1473 (تاریخ دقیق چاپ این کتاب قدیمی را تعیین نمی توان کرد).
69. در فصلی با عنوان «حرکت فلک هشتم»(De moto octavae sphaerae) برگها شماره ندارند.
70. " Albategni vero dicebat eas moveri uno gradu in sexaginta annis et quatuor mensibus semper versus orientem. "
71. قس. ص 264.
72. ر. ک. ص261.
73. مثلاً. ر. ک.
Copernicus, De revolutionibus, III, 13.
74. ر. ک. پانوشت شماره 16.
75. ر. ک. پانوشت شماره 19.
76. ر. ک. پانوشت شماره 1.
77. ر. ک. ص 258.
78. Staatsbibliothek, MS no. 5875; see W. Ahlwardt, Verzeichniss der arabischen Handschriften der Kgl. Bibliothek zu Berlin, V, 273 f.
این نسخه که در حدود 1397/800 به دست احمد بن تمیم نوشته شده و دارای 62 برگ است؛ فاقد صفحه عنوان و صفحات اول متن است. درآخر کتاب جمله غلط «تم کتاب الاربعه [کذا] شرح البَتّانی» آمده که بی شک به کتاب الاربعه بطلمیوس اشاره دارد. به گفته ی الوارت، تقسیم بندی کتاب به چهار مقاله و نیز مشخص کردن بخشهایی با عنوان شرح در این کتاب دیده نمی شود. چنانکه نلینو (I ,xxi ff) نشان داده است، مباحث مورد بحث و ترتیب آنها، با چند استثناء با کتاب الاربعه تطابق دارد.
79. ر. ک. پانوشت شماره 21.
I, 399: "Cod. CMLXVI, nr. 2°' : Commentarius in Quadripartitum Ptolemaei de astrorum iudiciis: subiectis tabulis. Auctor est vir clarissimus Mohammad Ben Geber Albategnius. "
80. Les manuscrits arabes de l'Escurial (Paris, 1884) , I, xxiv.
81. O. A. , I, xxiii.
82. "Les manuscrits arabes de l'Escurial decrits d'apres les notes de Hartwig Derenbourg," in Publications de l'Ecole Nationale des Langues Orientales Vivantes, 6th ser, 5, 2 fasc. 3 (1941) , 116.
83. O. A. , I, xxiii.
84. Cited after the anonymous Latin translation C. Ptolemaei de praedictionibus astronomicis, cui titulum fecerunt Quadripartitum, libri IV. Ed. posterior (Frankfurt, 1622).
85. این نسخه ی مهم را فؤاد سزگین، مؤسسه تاریخ علوم دانشگاه فرانکفورت، کشف کرده است. تاریخ آن قرن ششم /سیزدهم است.
86. استانبول، جارالله، 1499، برگ 81 پشت، نوشته شده در 1278/677. فقط یک صفحه است این نسخه را فؤاد سزگین کشف کرده است.
87. ر. ک. ص 265.
88. O. A. , I, xxiii-xxxi.
به آثار زیر از نلینو رجوع کنید:
C. A. Nallino: Al-Battani... Opus astronomicum (see note 3) ; "Al- Battani," in Encyclopaedia of Islam, Vol. I, repr. with augmentd bibliogrphy, ibid. , 2nd ed. , Vol. I; "Astronomy," ibid. ; "Astrologia e astronomia presso i Musulmani," in his Raccolta di scritti editi e inediti, Maria Nallino, ed. , V (Rome, 1944) , 1-87, esp. 52; "Storia dell'astronomia presso gli Arabi nel Medio Evo," ibid. , pp. 88-329, trans. by Maria Nallino from the Arabic original, Ilm al-Falak. . . (Rome, 1911-1912) ; and "Albatenio," in Enciclopedia italiano, repr. his Raccolta, V, 334-336;
کرلو الفونسو نلینو، تاریخ نجوم اسلامی، ترجمه احمد آرام. تهران، 1348. همچنین ر. ک.
H. Suter, "Die astronomischen Tafeln des Muhammad Ibn Musa al-Khwarizmi," in Det Kgl. Danske Videnskabernes Selskabs Skrifter, 7. Raekke, Historisk og Filologisk Afdeling, 3, no. 1 (1914) ; J. M. Millas-Vallicrosa, Estudios sobre Azerquiel (Madrid-Granada, 1943-1950) ; E. Honigmann, "Bemerkungen zu den geographischen Tabellen al-Battanis," in Rivista degli studi orientali, 11 (1927) , 169-175; and E. S. Kennedy and Muhammad Agha. "Planetary Visibility Tables in Islamic Astronomy," in Centarus, 7 (1960) , 134-140.
منبع مقاله :
گیلسپی، چارلز کولستون؛ (1389)، زندگینامه‌ی علمی دانشمندان اسلامی (جلد نخست)، ترجمه‌ی جمعی از مترجمان، تهران، شرکت انتشارات علمی و فرهنگی، چاپ چهارم.
