تاریخ مختصر حساب دیفرانسیل و انتگرال ( حسابان)

اغلب گفته می شود که نیوتن و لایبنیتز حسابان را اختراع کردند تا مسائلی چند را در دنیای فیزیکی حل کنند. شاهدی برای این ادعا وجود ندارد. در واقع نیوتن و لایبنیتز همچون اسلاف خود کنجکاو شدند تا مسأله ی « مماس» و مسأله « مساحت» را حل کنند، یعنی روش کلی برای یافتن مماس و مساحت به دست آورند؛ و پس از آن که حسابان به وجود آمد، در زمینه های مختلف به ویژه فیزیک به کار گرفته شد و موفقیت های شایانی به همراه آورد. توابع، حد، پیوستگی، مشتق، انگرال نامعین و قضیه ی اساسی حسابان ( که دو مورد اخیر را به هم پیوند می دهد) شالوده ی آن را تشکیل می دهند. البته این ترتیب ارتباط اندکی با نظمی که تحت آن این مفاهیم توسعه یافته اند دارد.
سرچشمه ی حسابان به دو هزار سال قبل و به کار یونانیان بر روی مماس و مساحت بر می گردد. ارشمیدس به روش افناء، مساحت قطعه ای از یک سهمی را به دست آورد، کاری که بر حسب اصطلاحات امروزی ما، همان برآورد تقریبی 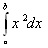است. وی همچنین مساحت یک بیضی و نیز حجم و مساحت سطح یک کره را به دست آورد. آپولونیوس درباره ی مماس های بر بیضی، سهمی و هذلولی مطالبی نوشت و ارشمیدس بحثی در مورد مماس های بر منحنی
موسوم به مارپیچ ارشمیدس ارائه کرد. آن ها انتظار اندکی داشتند که مسأله ی « مساحت» و مسأله ی « مماس» بتوانند چند قرن بعد به نقطه ی مشترکی برسند.
با فروپاشی جهان یونانی که بسته شدن آکادمی هزار ساله ی افلاطون در 529 بعد از میلاد به دست ژوستین نشانه آن بود، جهان اسلام حافظ کارهای ریاضی دانان یونانی شد، در یک محیط آزادطلبه های یهودی، مسلمان و مسیحی با یکدیگر کار می کردند، بر روی نوشته های قدیم شرح می نوشتند یا آن ها را ترجمه می کردند و گاهی نیز به آن ها شاخ و برگ تازه ای می دادند. به عنوان مثال الهازن حجم بعضی اجسام را محاسبه کرد و در واقع 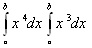را برآورد نمود.
مدرسیان قرن 14 سؤال زیر را مطرح کردند:
« اگر جسمی با سرعت متغیر حرکت کند، چه مسافتی را در یک مدت معین طی خواهد کرد؟»
و در همان دوره عده ای از جمله نیکول ارسم به حل آن پرداختند. گالیله نیز بعدها به مطالعه ی این مسأله همت گماشت.
به قرن هفدهم نکشید که چندین ایده به هم درآمیخت و حسابان را به وجود آورد. در سال 1637 دکارت و فرما هندسه تحلیلی را معرفی کردند. دکارت یک منحنی مفروض را به کمک روش های جبری مورد بررسی قرار داد، در حالی که فرما روشی برعکس را برگزید تا هندسه ی نهان در یک معادله ی مفروض را کشف نماید. به عنوان مثال، فرما نشان داد که نمودار 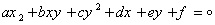همیشه یک بیضی، هذلولی، سهمی یا یکی از اشکال تباهیده ی آن هاست. در همین دوره، کاوالیری مساحت زیر منحنی 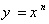را به ازای
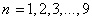به روشی که طول محاسباتش وقتی نما افزایش می یافت به سرعت رشد می کرد، به دست آورد. سپس حدس زد که الگوی به دست آمده برای نماهای بزرگتر نیز برقرار است. در طی بیست سال بعد، چندین ریاضی دان حدس او را تأیید کردند. بنابراین حتی محاسبه ی مساحت زیر منحنی به ازای یک عدد صحیح مثبت n، که اینک برای ما مسلم است، یک برگ برنده برای ریاضی دانان محسوب می شد. اما در مورد نمادهای دیگر چه می توان گفت؟ قبل از سال 1665 نمای دیگری مطرح نبود. با این حال ممکن بود با تابعی که با ضابطه ی 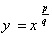، به ازای اعداد صحیح مثبت p و q تعریف می شود به عنوان تابع y که کار شود ( برای مثال تابع 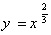تابعی است که ).
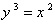والیس به وسیله ی روشی که بیشتر به جادو شباهت داشت تا ریاضیات، مساحت را پیدا کرد، با این حال فرما همین نتیجه را به کمک یک سری نامتناهی به دست آورد.
مسأله ی تعیین مماس بر یک منحنی نیز تا نیمه ی اول قرن هفدهم در ابهام بود. دکارت نشان داد چگونه قائم بر یک منحنی در نقطه ای مانند p را ( به کمک دایره ای که منحنی را فقط در p قطع می کند) می توان به دست آورد و بنابراین مماس، خطی است مار بر p و عمود بر آن خط. فرما مماس را به روشی مشابه روش کنونی ما به دست آورد و آن را در مسائل حداکثر – حداقل به کار برد.
قدم بعدی در مورد ترکیب روش های « مماس» و « مساحت» برداشته شد. در واقع بارو، معلم نیوتن در کمبریج، نتیجه ای معادل قضیه ی اساسی حسابان به دست آورد، اما آن را به شکلی سودمند بیان نکرد.
نیوتن در سال 1661 وارد کمبریج شد و در طی سال های 1665 و 1666 که در مزرعه ی خانوادگیش به سر می برد تا از طاعون در امان باشد مبانی حسابان را تکامل بخشید. وی دریافت که یافتن مماس و محاسبه مساحت دو فرآیند عکس یکدیگرند. گرچه اولین جدول انتگرال که تدوین شد در یکی از دست نوشته های نیوتن در این دوره به دست آمده است ولی وی نیز در آن زمان نتایج کار خود را منتشر نکرد که شاید علت آن کسادی بازار کتاب بعد از آتش سوزی بزرگ لندن در سال 1665 بود. در طول آن دو سال با ارزش، وی نماهای منفی و کسری را معرفی کرد. در واقع وی نشان داد که عملیات گوناگونی همچون ضرب یک عدد a چندین بار در خودش، معکوس کردنش و پیدا کردن ریشه ی بعضی از توان های آن عدد، دقیقاً موارد خاصی از یک تابع نمایی کلی هستند که در آن به ترتیب x یک عدد صحیح مثبت، 1- یا یک کسر است.
با این حال لایبنیتز به طور مستقل حسابان را ابداع کرد. او وکیل، سیاستمدار و فیلسوف بود و برای وی ریاضیات یک مشغله ی جدی به حساب می آمد، در سال های 1673 تا 1676 حسابان خود را طرح کرد و تحقیقاتش را در سال 1684 و 1686، واقعاً قبل از اولین انتشار نیوتن در سال 1711، منتشر کرد. وضع نمادهای dx و dy، اصطلاحات « حساب دیفرانسیل» و « حساب انتگرال»، علامت انتگرال و کلمه ی تابع را مدیون لایبنیتز هستیم. که برای نمایش مشتق گیری نسبت به زمان در فیزیک کنونی استفاده می شود تنها نمادی است که از نیوتن باقی مانده است.
بیش از دو قرن طول کشید تا این حسابان به وضعیت فعلی خود از لحاظ دقت و صحت رسید. مفهوم تابع از « منحنی» به تدریج به « دستور» یا قاعده ای که مقداری را به مقدار دیگری نسبت می دهد، تبدیل شد. کتاب درسی بزرگ حسابان اویلر که در 1748 منتشر شد بر تعریفی از تابع که در آن ذکری از نمودار نشده بود تأکید می کرد.
کوشی در سال های 1820، « حد» و « تابع پیوسته» را به مفهومی که امروزه به کار می بریم تعریف کرد. او همچنین تعریفی از انتگرال معین ارائه داد که با تغییری اندک به وسیله ی ریمان در سال 1825 به تعریف استاندارد فعلی تبدیل شد و به این ترتیب بود که در اواسط قرن نوزدهم اکتشاف های نیوتن و لایبنیتز بنیانی محکم به خود گرفتند.
در 1833، لیوویل نشان داد که قضیه ی بنیادی حسابان نمی تواند برای تعیین انتگرال همه ی توابع مقدماتی به کار رود. در حقیقت او نشان داد که تنها مقادیر k که به ازای آن ها 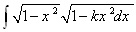تابعی مقدماتی است صفر و یک هستند. هنوز بعضی از سؤال های اساسی باقی مانده بود. مانند این که « منظور از مساحت چیست؟» ( برای مثال، آیا مجموعه ی نقاط داخل یک مربع که مختصات گویا دارند، دارای مساحت است یا نه؟) سال 1887 بود که پئانو تعریف دقیقی از مساحت ( کمیتی که ریاضی دانان پیشین به طور شهودی به آن می نگریستند) ارائه داد.
سرانجام مبانی حسابان با ارائه ی یک پایه ی استوار توسط ددکیند برای دستگاه اعداد حقیقی بر مبنای نظریه ی مجموعه های ( نامتناهی) کانتور مستحکم گردید.
بنابراین تاریخ حسابان شامل سه دوره است:
نخست این که برای مدت ها هیچ ملاحظه ای دال بر ارتباط مساحت و مماس وجود نداشت. در دوره ی بعد، از اواخر قرن هفدهم تا پایان قرن هجدهم، کشف ارتباط بسیار نزدیک آن ها و بهره وری از این ارتباط را شاهد هستیم. سرانجام به دنبال این دوره قرنی آمد که در آن بنیان های سست محکم شدند.
قرن بیستم حسابان را درک کرده و در بسیاری از حوزه های جدید به کار برده است. زیرا حسابان زبانی طبیعی است که با فرآیندهای پیوسته از قبیل تغییرات همراه با زمان سروکار دارد. حسابان به طور قطع زنده و همچنان باقوت در حال رشد است.

پی نوشت :

1- عضو هیات علمی دانشگاه فردوسی مشهد

منبع مقاله :
فلسفه ریاضی: کلاسیک، مدرن، پست مدرن صال مصلحیان، محمد؛ (1384) فلسفه ریاضی: کلاسیک، مدرن، پست مدرن، با ویرایش دکتر مجید میرزا وزیری، تهران، واژگان خرد، چاپ نخست.