
نویسنده: گراهام پریست
مترجم: بهرام اسدیان
مترجم: بهرام اسدیان
وقت آن رسیده که به مسئله ی اعتبار استقرار برگردیم؛ یعنی اعتبار آن استنتاج هایی که گرچه مقدمه ها دلیلی برای نتیجه به دست می دهند، ولی حتی اگر این مقدمه ها صادق باشند، نتیجه همچنان ممکن است کاذب از آب در آید.
همان طور که در فصل اول گفتم، شرلوک هولمز دراین نوع استنتاج ها بسیارماهر بود. پس بهتر است کار را با او شروع کنیم. معمای انجمن موسرخ ها زمانی مطرح می شود که هولمز ودکتر واتسن با آقای جَبِز ویلسن ملاقات می کنند. وقتی ویلسن وارد می شود، واتسن مشتاق می شود که ببیند هولز چه چیزهایی درباره ی او استنتاج کرده است:
«چیزی بیش تر ازچند نکته ی واضح، از قبیل این که ایشان در یک دوره از زندگی خود کار یدی می کرده، وانفیه مصرف می کند و این که فراماسون است و این که در چین اقامت داشته و اخیراً هم مقدار زیادی چیز نوشته، بله چیزی بیش تر از این چند نکته نمی توانم استنتاج کنم.»
آقای ویلسن بهت زده بر صندلی خود میخکوب شد؛ انگشت اشاره اش هنوز روی روزنامه بود ولی سرش را بلند کرده به مصاحب من می نگریست.
پرسید: «آقای هولمز، شما را به فرشته ی اقبال سوگند، به من بگویید این اطلاعات را از کجا به دست آورده اید.» (1)
هولمز با شور و علاقه توضیح می دهد. مثلاً درباره ی این که چه طور فهمیده آقای ویلسن اخیراً مقدار زیادی چیز نوشته، می گوید:
«وقتی سرآستین راست شما به اندازه ی سه چهار بند انگشت براق شده و آستین چپ شما نزدیک آرنج، همان جایی که آن را روی میز تحریر تکیه می دهید، ساییده شده چه نتیجه گیری دیگری می توانم بکنم؟» (2)
با این که هولمز خیلی دلش می خواهد به این جور استنتاج، استنتاج قیاسی بگوید، ولی استنتاج در واقع استقرایی است. کاملاً ممکن است که در کت ویلسن واقعاً این نشانه ها دیده شود بی آن که او زیاد چیز نوشته باشد. مثلاً، شاید او این کت را از کسی دزدیده که نویسنده بوده. با این حال، قطعاً استنتاجِ بسیار خوبی است. چه چیزی باعث می شود که این جور استنتاج ها استنتاج های خوبی محسوب شوند؟ یک راه خوب برای پاسخ به این سؤال این است که از احتمالات کمک بگیریم. پس بیایید درباره ی احتمال صحبت کنیم، تا بعد درباره به این سؤال برگردیم.
احتمال عددی است که به یک جمله نسبت می دهیم. این عدد در واقع میزان احتمال آن جمله را نشان می دهد. احتمال a را با (pr (a نشان می دهیم. به رسم قرار داد، احتمال ها را در طیفی میان 0 و 1 می سنجیم. اگر 0=)(a) pr، آنگاه a، قطعاً کاذب است. در نتیجه، هر قدر pr (a) بالاتر برود، احتمال این که a صادق باشد بیش تر می شود. اگر pr (a)=1، آنگاه a قطعاً صادق است.
درباره ی این اعداد، دیگر چه می توان گفت؟ اجازه دهید مثالی بزنیم.
روزهای هفته را در نظر بگیرید. فرض کنید w جمله ای است که در هر روز یا صادق است یا کاذب- مثلاً این جمله:«هوا گرم است». r هم همین طور است- مثلاً این جمله «باران می آید». جدول زیر اطلاعات ما را نشان می دهد.
 علامت تیکی که زیر بعضی از روزها آمده نشان دهنده ی این است که جمله در آن روز صادق است. اگرهیچ علامتی نباشد، یعنی جمله در آن روز کاذب است.
علامت تیکی که زیر بعضی از روزها آمده نشان دهنده ی این است که جمله در آن روز صادق است. اگرهیچ علامتی نباشد، یعنی جمله در آن روز کاذب است.
خب، ازهمین هفته ی به خصوص یک روز را به طور تصادفی انتخاب کنید؛ چه قدر احتمال دارد که آن روز هوا گرم باشد؟ از بین هفت روزِ هفته چهار روزِ گرم داریم. پس احتمال گرم بودن ، است. از طرف دیگر، سه روزِ بارانی داریم. پس احتمال بارانی بودن
است. از طرف دیگر، سه روزِ بارانی داریم. پس احتمال بارانی بودن است:
است:

 به طور کلی، اگر تعداد روزهایی را که در آن ها جمله ی a صادق است با a# و تعداد
به طور کلی، اگر تعداد روزهایی را که در آن ها جمله ی a صادق است با a# و تعداد
کل روزها را با N نشان دهیم، خواهیم داشت:
 احتمال چگونه به نقیض، ترکیب عطفی، و ترکیب فصلی مربوط می شود؟
احتمال چگونه به نقیض، ترکیب عطفی، و ترکیب فصلی مربوط می شود؟
اول برویم سروقت نقیض. در مثال بالا، احتمال چه قدر است؟ می دانیم که سه روز هوا گرم نیست، پس )
چه قدر است؟ می دانیم که سه روز هوا گرم نیست، پس ) . توجه داشته باشید که جمع pr(w) و
. توجه داشته باشید که جمع pr(w) و عدد 1 می شود. این اصلاً تصادفی نیست. به طور کلی:
عدد 1 می شود. این اصلاً تصادفی نیست. به طور کلی:  اگر دو طرف تساوی را بر N تقسیم کنیم،خواهیم داشت:
اگر دو طرف تساوی را بر N تقسیم کنیم،خواهیم داشت:
 که یعنی:
که یعنی:  و اما ترکیب عطفی و فصلی. دو روز داریم که هوا هم گرم است و هم بارانی. پس
و اما ترکیب عطفی و فصلی. دو روز داریم که هوا هم گرم است و هم بارانی. پس = pr(w&r) . پنج روز هم داریم که در آن ها هوا یا گرم است یا بارانی. پس
= pr(w&r) . پنج روز هم داریم که در آن ها هوا یا گرم است یا بارانی. پس = pr(w∨ r) . بین این دو عدد [یعنی بین
= pr(w∨ r) . بین این دو عدد [یعنی بین چه نسبتی برقرار است؟ برای این که بفهمیم چند روز هست که (w∨ r) در آن ها صادق است، می توانیم اول روزهایی را که در آن ها W صادق است بشماریم، و بعد تعداد روزهایی را که در آن ها r صادق است به آن روزها اضافه کنیم ولی با این کار به جواب درست نمی رسیم، چون چند روز را دوبار شمرده ایم( چهارشنبه و شنبه را). و این ها روزهای هستند که هم بارانی اند و هم گرم. پس برای این که به جواب برسیم، باید تعداد روزهایی را که هم بارانی اند و هم گرم کم کنیم:
چه نسبتی برقرار است؟ برای این که بفهمیم چند روز هست که (w∨ r) در آن ها صادق است، می توانیم اول روزهایی را که در آن ها W صادق است بشماریم، و بعد تعداد روزهایی را که در آن ها r صادق است به آن روزها اضافه کنیم ولی با این کار به جواب درست نمی رسیم، چون چند روز را دوبار شمرده ایم( چهارشنبه و شنبه را). و این ها روزهای هستند که هم بارانی اند و هم گرم. پس برای این که به جواب برسیم، باید تعداد روزهایی را که هم بارانی اند و هم گرم کم کنیم:
Pr(w v r)= #w + #r - #( w&r)اگر دو طرف تساوی را برN تقسیم کنیم، خواهیم داشت: که یعنی:
که یعنی:
Pr(w v r)= pr(w) + pr(r) - pr(w&r)و این رابطه ای کلی ای است که بین احتمالِ ترکیب های فصلی وعطفی برقرار است
که درجات صدق را نیز می توان با اعداد میان 0 و 1 اندازه گرفت. پس شاید به این نتیجه برسید که درجات صدق و احتمالات یک چیزند؛ ولی یک چیز نیستند. رفتار ترکیب فصلی و عطفی خیلی با هم فرق می کند. در بحث درجات صدق، ترکیب فصلی تابع ارزش است. می دانیم که |w ∨r| ماکسیمم |r|و |w| است. ولی همان طور که کمی بالاتر دیدیم، pr(w v r) ( را نمی توانیم صرفاً از روی pr(w) و ( pr (r به دست آوریم .دیدیم که
 قبل از آن که به استناد های استقرایی برگردیم، باید به چند نکته ی کوچک دیگر اشاره کنیم. برگردیم به همان هفته ی کذایی. احتمال این که یکی از روزها- که کاملاً هم تصادفی انتخاب شده- بارانی باشد
قبل از آن که به استناد های استقرایی برگردیم، باید به چند نکته ی کوچک دیگر اشاره کنیم. برگردیم به همان هفته ی کذایی. احتمال این که یکی از روزها- که کاملاً هم تصادفی انتخاب شده- بارانی باشد است. ولی فرض کنید که شما می دانید آن روز از روزهای گرم هفته است. حالا احتمال این که آن روز بارانی باشد چه قدر است؟ می دانیم کلاً چهار روز گرم داریم که فقط دو روزش بارانی است. پس احتمال
است. ولی فرض کنید که شما می دانید آن روز از روزهای گرم هفته است. حالا احتمال این که آن روز بارانی باشد چه قدر است؟ می دانیم کلاً چهار روز گرم داریم که فقط دو روزش بارانی است. پس احتمال است. به این حالت احتمال شرطی(3) می گویند، و به این شکل نشانش می دهند:
است. به این حالت احتمال شرطی(3) می گویند، و به این شکل نشانش می دهند:
( pr(r |w)، که یعنی احتمال r به شرط یا با فرضw. با کمی تأمل، به راحتی می توانیم فرمولی کلی برای احتمالات شرطی پیدا کنیم. چگونه به رسیدیم؟ اول فقط روزهایی را درنظر گرفتیم که درآن هاw صادق است؛ بعد دیدیم که در کدام روزها هم wصادق است و هم r. درآخر هم، تعداد این روزها را بر تعداد روزهایی که w در آن ها صادق است تقسیم کردیم:
رسیدیم؟ اول فقط روزهایی را درنظر گرفتیم که درآن هاw صادق است؛ بعد دیدیم که در کدام روزها هم wصادق است و هم r. درآخر هم، تعداد این روزها را بر تعداد روزهایی که w در آن ها صادق است تقسیم کردیم:
 اندکی آشنایی با جبر به ما نشان می دهد که این جمله با جمله ی زیر مساوی است:
اندکی آشنایی با جبر به ما نشان می دهد که این جمله با جمله ی زیر مساوی است:
 و این یعنی pr(w) ÷ (pr(w&r.
و این یعنی pr(w) ÷ (pr(w&r.
فرمول کلی احتمالات شرطی پیدا شد:
cp:pr( w |r)=pr(w&r)/pr(w)
در کاربرد این فرمول باید کمی احتیاط به خرج داد. تقسیم عدد بر 0 بی معناست. مثلاً هیچ ارزشی ندارد [نه صادق است نه کاذب].
هیچ ارزشی ندارد [نه صادق است نه کاذب].
ریاضیدانان به این نسبت، نسبت تعریف نشده می گویند. در فرمولcp، ( pr(w & r
را برpr(w) تقسیم کردیم. پس کل این فرمول وقتی معنی دارد که pr(w) صفر نباشد، یعنی فقط وقتی که w درلااقل یک روز صادق باشد. درغیر این صورت، احتمال شرطی تعریف نشده است.
حالا دیگر می توانیم برویم سراغ استنتاج های استقرایی. استتاج استقرایی چه وقت معتبراست؟ ساده است، وقتی که مقدمه ها میزان احتمال نتیجه را بسیار بالا ببرند. یعنی وقتی احتمال شرطی c (نتیجه) با فرض یا به شرط p (مقدمه یا مجموعه ای ازترکیب های عطف مقدمات) بیش تر از احتمال نقیض c باشد:
 پس، با توجه به هفته ی کذایی مان، استنتاج
پس، با توجه به هفته ی کذایی مان، استنتاج
روزی بارانی بود؛ پس گرم بود.
از نظر استقرایی معتبر است. چون
 با این حرف ها می توانیم نشان دهیم که چرا استنتاج هولمز معتبر بود.
با این حرف ها می توانیم نشان دهیم که چرا استنتاج هولمز معتبر بود.
هولمز نتیجه گرفته بود که جبز ویلسن مقدار زیادی چیز نوشته (c). مقدمه دایر بر این بود که فلان نشانه ها روی کت ویلسن دیده می شوند(p). اگر به لندنِ آن روزگار برگردیم و همه ی کسانی را که آستین کتشان به چنان روزی درآمده کنار هم بگذاریم، متوجه می شویم که اکثریت آن ها کارمند بودند، یعنی کسانی که دائماً پشت میزمشغول نوشتن بودند. بنابراین، احتمال این که جبر مقدار زیادی چیز نوشته باشد، با این فرض که کتش این نشانه ها را دارد، بیش تر از این است که آن چیزها را ننوشته باشد. استنتاج هولمز از نظراستقرایی معتبر است.
این دم و دستگاهی که علم کردیم معضلی تولید می کند که من با اشاره ای به آن این فصل را به پایان می برم. همان طور که دیدیم، احتمال را می توان از طریق یک نسبت به دست آورد؛ به این شکل که اول مجموعه ی مرجع(4) معینی در نظر می گیریم؛ بعد تعدادِ گروه های مختلفِ درون آن را محاسبه می کنیم؛ و در آخر هم ضرب و تقسیم هایی می کنیم. ولی کدام مجموعه را باید مجموعه ی مرجع در نظر بگیریم؟ در مثال روزهای هفته، من پیش از هرکاری مجموعه ی مرجع را مشخص کردم: روزهای آن هفته ی خاص. اما مسائل در زندگی روزمره به این شکل مطرح نمی شوند.
به جبز ویلسن برگردیم. برای به دست آوردن احتمالات دراین مورد، پیشنهاد من این بود که مجموعه ی مرجع را آدم هایی بگیریم که در لندنِ روزگار هولمز زندگی می کردند. ولی آخر به چه دلیل؟ چرا آدم هایی را نگیریم که در کلِ انگلستان یا اروپای آن روزگار زندگی می کردند؟ چرا فقط مردان لندن را در نظر نگیریم، یا فقط آن هایی را که امکان ملاقات با هولمز را داشتند؟ شاید در چند مورد، چندان فرق اساسی ای ایجاد نشود. ولی مسلماً در مابقی موارد می شود. مثلاً، آدم هایی که به دیدنِ هولمز می آیند همگی ثروتمندند، و بنابراین، احتمالاً کت های دست دوم نمی پوشند. اگر دامنه ی آدم ها را گسترش دهیم، وضع حتماً خیلی فرق می کند. بالاخره مجموعه ی مرجع مناسب کدام است؟ این از آن جور سؤال هایی است که کارشناسان بیمه را تا صبح بیدار نگه می دارد.
در تحلیل آخر، احتمالاً به این نتیجه می رسیم که درست ترین مجموعه ی مرجع مجموعه ای است که فقط خود ویلسن را در برمی گیرد. آیا این یعنی اطلاعات ما درباره ی دیگران درنهایت هیچ ربطی به آن ها پیدا نمی کند؟ در این مورد خاص، او یا مقدار زیادی چیز نوشته یا اصلاً چیزی ننوشته. در حالت اول، احتمال این که او چیز نوشته، با فرض این که سرآستینی براق دارد، 1 است، و استنتاج معتبر است. در حالت دوم، احتمال 0 است، و استنتاج معتبر نیست. به عبارت دیگر، اعتبار استنتاج یکسره وابسته به صدق نتیجه است. پس شما نمی توانید استنتاج را به خدمت بگیرید تا تعیین کنید نتیجه صادق است یا نه. اگر تا این حد جلو بروید، مفهومی که از اعتبار نصیبتان می شود کاملاً بی فایده از آب درمی آید.
پریست، گراهام،(1386)، منطق، مترجم: بهرام اسدیان، تهران: نشر ماهی، چاپ سوم
همان طور که در فصل اول گفتم، شرلوک هولمز دراین نوع استنتاج ها بسیارماهر بود. پس بهتر است کار را با او شروع کنیم. معمای انجمن موسرخ ها زمانی مطرح می شود که هولمز ودکتر واتسن با آقای جَبِز ویلسن ملاقات می کنند. وقتی ویلسن وارد می شود، واتسن مشتاق می شود که ببیند هولز چه چیزهایی درباره ی او استنتاج کرده است:
«چیزی بیش تر ازچند نکته ی واضح، از قبیل این که ایشان در یک دوره از زندگی خود کار یدی می کرده، وانفیه مصرف می کند و این که فراماسون است و این که در چین اقامت داشته و اخیراً هم مقدار زیادی چیز نوشته، بله چیزی بیش تر از این چند نکته نمی توانم استنتاج کنم.»
آقای ویلسن بهت زده بر صندلی خود میخکوب شد؛ انگشت اشاره اش هنوز روی روزنامه بود ولی سرش را بلند کرده به مصاحب من می نگریست.
پرسید: «آقای هولمز، شما را به فرشته ی اقبال سوگند، به من بگویید این اطلاعات را از کجا به دست آورده اید.» (1)
هولمز با شور و علاقه توضیح می دهد. مثلاً درباره ی این که چه طور فهمیده آقای ویلسن اخیراً مقدار زیادی چیز نوشته، می گوید:
«وقتی سرآستین راست شما به اندازه ی سه چهار بند انگشت براق شده و آستین چپ شما نزدیک آرنج، همان جایی که آن را روی میز تحریر تکیه می دهید، ساییده شده چه نتیجه گیری دیگری می توانم بکنم؟» (2)
با این که هولمز خیلی دلش می خواهد به این جور استنتاج، استنتاج قیاسی بگوید، ولی استنتاج در واقع استقرایی است. کاملاً ممکن است که در کت ویلسن واقعاً این نشانه ها دیده شود بی آن که او زیاد چیز نوشته باشد. مثلاً، شاید او این کت را از کسی دزدیده که نویسنده بوده. با این حال، قطعاً استنتاجِ بسیار خوبی است. چه چیزی باعث می شود که این جور استنتاج ها استنتاج های خوبی محسوب شوند؟ یک راه خوب برای پاسخ به این سؤال این است که از احتمالات کمک بگیریم. پس بیایید درباره ی احتمال صحبت کنیم، تا بعد درباره به این سؤال برگردیم.
احتمال عددی است که به یک جمله نسبت می دهیم. این عدد در واقع میزان احتمال آن جمله را نشان می دهد. احتمال a را با (pr (a نشان می دهیم. به رسم قرار داد، احتمال ها را در طیفی میان 0 و 1 می سنجیم. اگر 0=)(a) pr، آنگاه a، قطعاً کاذب است. در نتیجه، هر قدر pr (a) بالاتر برود، احتمال این که a صادق باشد بیش تر می شود. اگر pr (a)=1، آنگاه a قطعاً صادق است.
درباره ی این اعداد، دیگر چه می توان گفت؟ اجازه دهید مثالی بزنیم.
روزهای هفته را در نظر بگیرید. فرض کنید w جمله ای است که در هر روز یا صادق است یا کاذب- مثلاً این جمله:«هوا گرم است». r هم همین طور است- مثلاً این جمله «باران می آید». جدول زیر اطلاعات ما را نشان می دهد.

خب، ازهمین هفته ی به خصوص یک روز را به طور تصادفی انتخاب کنید؛ چه قدر احتمال دارد که آن روز هوا گرم باشد؟ از بین هفت روزِ هفته چهار روزِ گرم داریم. پس احتمال گرم بودن ،
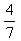 است. از طرف دیگر، سه روزِ بارانی داریم. پس احتمال بارانی بودن
است. از طرف دیگر، سه روزِ بارانی داریم. پس احتمال بارانی بودن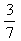 است:
است: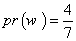
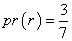
کل روزها را با N نشان دهیم، خواهیم داشت:
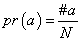
اول برویم سروقت نقیض. در مثال بالا، احتمال
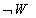 چه قدر است؟ می دانیم که سه روز هوا گرم نیست، پس )
چه قدر است؟ می دانیم که سه روز هوا گرم نیست، پس )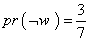 . توجه داشته باشید که جمع pr(w) و
. توجه داشته باشید که جمع pr(w) و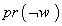 عدد 1 می شود. این اصلاً تصادفی نیست. به طور کلی:
عدد 1 می شود. این اصلاً تصادفی نیست. به طور کلی: 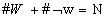 اگر دو طرف تساوی را بر N تقسیم کنیم،خواهیم داشت:
اگر دو طرف تساوی را بر N تقسیم کنیم،خواهیم داشت: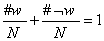
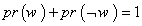 و اما ترکیب عطفی و فصلی. دو روز داریم که هوا هم گرم است و هم بارانی. پس
و اما ترکیب عطفی و فصلی. دو روز داریم که هوا هم گرم است و هم بارانی. پس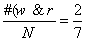 = pr(w&r) . پنج روز هم داریم که در آن ها هوا یا گرم است یا بارانی. پس
= pr(w&r) . پنج روز هم داریم که در آن ها هوا یا گرم است یا بارانی. پس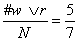 = pr(w∨ r) . بین این دو عدد [یعنی بین
= pr(w∨ r) . بین این دو عدد [یعنی بین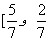 چه نسبتی برقرار است؟ برای این که بفهمیم چند روز هست که (w∨ r) در آن ها صادق است، می توانیم اول روزهایی را که در آن ها W صادق است بشماریم، و بعد تعداد روزهایی را که در آن ها r صادق است به آن روزها اضافه کنیم ولی با این کار به جواب درست نمی رسیم، چون چند روز را دوبار شمرده ایم( چهارشنبه و شنبه را). و این ها روزهای هستند که هم بارانی اند و هم گرم. پس برای این که به جواب برسیم، باید تعداد روزهایی را که هم بارانی اند و هم گرم کم کنیم:
چه نسبتی برقرار است؟ برای این که بفهمیم چند روز هست که (w∨ r) در آن ها صادق است، می توانیم اول روزهایی را که در آن ها W صادق است بشماریم، و بعد تعداد روزهایی را که در آن ها r صادق است به آن روزها اضافه کنیم ولی با این کار به جواب درست نمی رسیم، چون چند روز را دوبار شمرده ایم( چهارشنبه و شنبه را). و این ها روزهای هستند که هم بارانی اند و هم گرم. پس برای این که به جواب برسیم، باید تعداد روزهایی را که هم بارانی اند و هم گرم کم کنیم:Pr(w v r)= #w + #r - #( w&r)اگر دو طرف تساوی را برN تقسیم کنیم، خواهیم داشت:
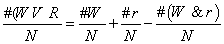 که یعنی:
که یعنی:Pr(w v r)= pr(w) + pr(r) - pr(w&r)و این رابطه ای کلی ای است که بین احتمالِ ترکیب های فصلی وعطفی برقرار است
که درجات صدق را نیز می توان با اعداد میان 0 و 1 اندازه گرفت. پس شاید به این نتیجه برسید که درجات صدق و احتمالات یک چیزند؛ ولی یک چیز نیستند. رفتار ترکیب فصلی و عطفی خیلی با هم فرق می کند. در بحث درجات صدق، ترکیب فصلی تابع ارزش است. می دانیم که |w ∨r| ماکسیمم |r|و |w| است. ولی همان طور که کمی بالاتر دیدیم، pr(w v r) ( را نمی توانیم صرفاً از روی pr(w) و ( pr (r به دست آوریم .دیدیم که
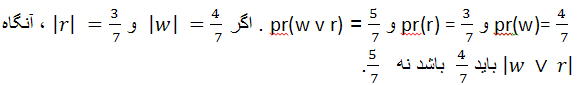
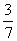 است. ولی فرض کنید که شما می دانید آن روز از روزهای گرم هفته است. حالا احتمال این که آن روز بارانی باشد چه قدر است؟ می دانیم کلاً چهار روز گرم داریم که فقط دو روزش بارانی است. پس احتمال
است. ولی فرض کنید که شما می دانید آن روز از روزهای گرم هفته است. حالا احتمال این که آن روز بارانی باشد چه قدر است؟ می دانیم کلاً چهار روز گرم داریم که فقط دو روزش بارانی است. پس احتمال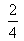 است. به این حالت احتمال شرطی(3) می گویند، و به این شکل نشانش می دهند:
است. به این حالت احتمال شرطی(3) می گویند، و به این شکل نشانش می دهند:( pr(r |w)، که یعنی احتمال r به شرط یا با فرضw. با کمی تأمل، به راحتی می توانیم فرمولی کلی برای احتمالات شرطی پیدا کنیم. چگونه به
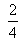 رسیدیم؟ اول فقط روزهایی را درنظر گرفتیم که درآن هاw صادق است؛ بعد دیدیم که در کدام روزها هم wصادق است و هم r. درآخر هم، تعداد این روزها را بر تعداد روزهایی که w در آن ها صادق است تقسیم کردیم:
رسیدیم؟ اول فقط روزهایی را درنظر گرفتیم که درآن هاw صادق است؛ بعد دیدیم که در کدام روزها هم wصادق است و هم r. درآخر هم، تعداد این روزها را بر تعداد روزهایی که w در آن ها صادق است تقسیم کردیم: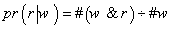
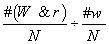
فرمول کلی احتمالات شرطی پیدا شد:
cp:pr( w |r)=pr(w&r)/pr(w)
در کاربرد این فرمول باید کمی احتیاط به خرج داد. تقسیم عدد بر 0 بی معناست. مثلاً
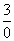 هیچ ارزشی ندارد [نه صادق است نه کاذب].
هیچ ارزشی ندارد [نه صادق است نه کاذب].ریاضیدانان به این نسبت، نسبت تعریف نشده می گویند. در فرمولcp، ( pr(w & r
را برpr(w) تقسیم کردیم. پس کل این فرمول وقتی معنی دارد که pr(w) صفر نباشد، یعنی فقط وقتی که w درلااقل یک روز صادق باشد. درغیر این صورت، احتمال شرطی تعریف نشده است.
حالا دیگر می توانیم برویم سراغ استنتاج های استقرایی. استتاج استقرایی چه وقت معتبراست؟ ساده است، وقتی که مقدمه ها میزان احتمال نتیجه را بسیار بالا ببرند. یعنی وقتی احتمال شرطی c (نتیجه) با فرض یا به شرط p (مقدمه یا مجموعه ای ازترکیب های عطف مقدمات) بیش تر از احتمال نقیض c باشد:
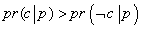
روزی بارانی بود؛ پس گرم بود.
از نظر استقرایی معتبر است. چون
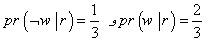
هولمز نتیجه گرفته بود که جبز ویلسن مقدار زیادی چیز نوشته (c). مقدمه دایر بر این بود که فلان نشانه ها روی کت ویلسن دیده می شوند(p). اگر به لندنِ آن روزگار برگردیم و همه ی کسانی را که آستین کتشان به چنان روزی درآمده کنار هم بگذاریم، متوجه می شویم که اکثریت آن ها کارمند بودند، یعنی کسانی که دائماً پشت میزمشغول نوشتن بودند. بنابراین، احتمال این که جبر مقدار زیادی چیز نوشته باشد، با این فرض که کتش این نشانه ها را دارد، بیش تر از این است که آن چیزها را ننوشته باشد. استنتاج هولمز از نظراستقرایی معتبر است.
این دم و دستگاهی که علم کردیم معضلی تولید می کند که من با اشاره ای به آن این فصل را به پایان می برم. همان طور که دیدیم، احتمال را می توان از طریق یک نسبت به دست آورد؛ به این شکل که اول مجموعه ی مرجع(4) معینی در نظر می گیریم؛ بعد تعدادِ گروه های مختلفِ درون آن را محاسبه می کنیم؛ و در آخر هم ضرب و تقسیم هایی می کنیم. ولی کدام مجموعه را باید مجموعه ی مرجع در نظر بگیریم؟ در مثال روزهای هفته، من پیش از هرکاری مجموعه ی مرجع را مشخص کردم: روزهای آن هفته ی خاص. اما مسائل در زندگی روزمره به این شکل مطرح نمی شوند.
به جبز ویلسن برگردیم. برای به دست آوردن احتمالات دراین مورد، پیشنهاد من این بود که مجموعه ی مرجع را آدم هایی بگیریم که در لندنِ روزگار هولمز زندگی می کردند. ولی آخر به چه دلیل؟ چرا آدم هایی را نگیریم که در کلِ انگلستان یا اروپای آن روزگار زندگی می کردند؟ چرا فقط مردان لندن را در نظر نگیریم، یا فقط آن هایی را که امکان ملاقات با هولمز را داشتند؟ شاید در چند مورد، چندان فرق اساسی ای ایجاد نشود. ولی مسلماً در مابقی موارد می شود. مثلاً، آدم هایی که به دیدنِ هولمز می آیند همگی ثروتمندند، و بنابراین، احتمالاً کت های دست دوم نمی پوشند. اگر دامنه ی آدم ها را گسترش دهیم، وضع حتماً خیلی فرق می کند. بالاخره مجموعه ی مرجع مناسب کدام است؟ این از آن جور سؤال هایی است که کارشناسان بیمه را تا صبح بیدار نگه می دارد.
در تحلیل آخر، احتمالاً به این نتیجه می رسیم که درست ترین مجموعه ی مرجع مجموعه ای است که فقط خود ویلسن را در برمی گیرد. آیا این یعنی اطلاعات ما درباره ی دیگران درنهایت هیچ ربطی به آن ها پیدا نمی کند؟ در این مورد خاص، او یا مقدار زیادی چیز نوشته یا اصلاً چیزی ننوشته. در حالت اول، احتمال این که او چیز نوشته، با فرض این که سرآستینی براق دارد، 1 است، و استنتاج معتبر است. در حالت دوم، احتمال 0 است، و استنتاج معتبر نیست. به عبارت دیگر، اعتبار استنتاج یکسره وابسته به صدق نتیجه است. پس شما نمی توانید استنتاج را به خدمت بگیرید تا تعیین کنید نتیجه صادق است یا نه. اگر تا این حد جلو بروید، مفهومی که از اعتبار نصیبتان می شود کاملاً بی فایده از آب درمی آید.
پی نوشت ها :
با اندکی تغییر به نقل از ترجمه ی فارسی: کانن دویل، آرتور، رسوایی در بوهِم، ترجمه ی کریم امامی، تهران، طرح نو، ص .58.م
همان، ص 59.
2- Conditional probability
3-reference class
پریست، گراهام،(1386)، منطق، مترجم: بهرام اسدیان، تهران: نشر ماهی، چاپ سوم
















