

نویسنده: Moshe Livšič
مترجم: مجید ملکان
مترجم: مجید ملکان
[nāum ilyičāxiezer]
Naum Il"ich Akhiezer
(ت. چریکوف، روسیهی سفید، 15 اسفند 1279 / 6 مارس 1901؛ و. خارکف، روسیه، 13 خرداد 1359 / 3 ژوئن 1980)، ریاضیات.
آخیئزر در سال 1302 از «مؤسسهی آموزش مردمی کییف» فارغالتحصیل شد، و بعد در دانشگاه کییف تحصیلات خود را برای اخذ درجهی نامزدی تحت نظارت د.آ. گراوی، که از نامداران رشتهی جبر بود، ادامه داد. او در پایاننامهی نامزدی خود، که به پژوهش در زمینهی آئرودینامیک اختصاص یافته بود، روشهای آنالیز مختلط را در مسائل آئرو دینامیک بکار بست. وی اولین کسی بود که فورمولی برای نگاشت همدیس دامنهی کثیرالاضلاعی دارای همبندی مضاعف به یک حلقه بدست آورد.
آخیئزر سخت درگیر مسائل نظریهی تقریب بود. در 1307 مسألهی دشواری را حل کرد: در میان همهی چند جملهایهای درجهی n، که ضرایب سه جمله از بالاترین درجات آن ثابت است، در بازهی معینی از محور حقیقی کمترین انحراف نسبت به چند جملهایِ صفر را پیدا کنید. آخیئزر نشان داد که راه حل این مسأله را میتوان به کمک توابع شوتکی بدست آورد. این نتیجه انگیزهی بحثی شد برای گسترش هرچه بیشتر نظریهی کلاسیک حداقل انحراف نسبت به چند جملهایهای صفر، که پ. ل. چیبیشوف، ن. زلتاریوف، و و.ا. مارکف عرضه کرده بودند. آخیئزر بعداً نشان داد که مسأله حداقل انحراف نسبت به چند جملهای صفر را در حالتی که k ضریب از ضرایب درجات بالای آن ثابتند میتوان به مسألهی یافتن حوزهای که همراه k برشهای قطعهای در امتداد محور حقیقی صفحهی مختلط باشد، و نیز به ساختنِ تابع گرینِ این حوزه، تقلیل داد.
آخیئزر در 1312 به خارکف نقفل مکان کرد، و در آنجا سالها سرپرست بخش آنالیز مختلط و رئیس «انجمن ریاضی خارکف» بود. در 1313 به عضویت مکاتبهای «فرهنگستان علوم اوکراین» انتخاب شد. در آن زمان آخیئزر و م. کرین شروع به بررسی مسألهی –L مؤمان کردند: مطلوب است چگالیِ توزیع جرمی با موْمانهای معلوم که شرط اضافی
چگالیِ توزیع جرمی با موْمانهای معلوم که شرط اضافی در آن صدق کند. خلاصهی پژوهشهای آنان در این زمینه در Some Questions in the Theory of Moments («پرسشهائی دربارهی نظریهی موْمانها»، 1933) مندرج است. آنان همچنین با چند جملهایهای مثلثاتی به مقدار دقیق یک ثابت در قضیهی دانم جکسن در مورد تقریب تابع متناوب پیبردند (این مقدار را ژان فاوار مستقلاً یافته بود).
در آن صدق کند. خلاصهی پژوهشهای آنان در این زمینه در Some Questions in the Theory of Moments («پرسشهائی دربارهی نظریهی موْمانها»، 1933) مندرج است. آنان همچنین با چند جملهایهای مثلثاتی به مقدار دقیق یک ثابت در قضیهی دانم جکسن در مورد تقریب تابع متناوب پیبردند (این مقدار را ژان فاوار مستقلاً یافته بود).
آخیئزر در جریان جنگ جهانی دوم در «مؤسسهی معدنکاوی آلماآتا» (1320-1322) و «مؤسسهی مهندسی نیروی مسکو» (1322-1326) کار میکرد. در 1326، یعنی سالی که کتاب او دربارهی نظریهی تقریب منتشر شد، به خارکف بازگشت. او در این کتاب عقاید جدید مربوط به آنالیز تابعی را با روشهای کلاسیک درآمیخت و نتایج کار خودش را عرضه کرد. در 1328 جایزهی چیبیسوف به مناسبت این کتاب به او اعطا شد.
الهامبخش پژوهشهای بیشتر در این زمینه س.ن. برنشتاین – یکی از بنیادگذاران نظریهی تقریب – بود، که در 1303 مسألهی زیر را فوْرمولبندی کرده بود: فرض کنید
 تابعی باشد که
تابعی باشد که و
و . حال فضای CØ از توابع پیوستهی ƒ(t) را چنان تعریف میکنیم که
. حال فضای CØ از توابع پیوستهی ƒ(t) را چنان تعریف میکنیم که و فرض میکنیم که
و فرض میکنیم که

هنج واقع در CØ باشد. شرایط لازم و کافی برای Ø را چنان پیدا کنید که چند جملهایها مجموعهای چگال از CØ را تشکیل دهند. آخیئزر و ک. بابنکو، در کار مشترک خود بر سر این مسأله، MØ دستهی مهمی از چند جملهایهای P(x) را که در نامساوی صدق میکردند بررسی نمودند و عبارت زیر را بدست آوردند
صدق میکردند بررسی نمودند و عبارت زیر را بدست آوردند

در 1332 آخیئزر و برنشتاین دریافتند که ، که در آن
، که در آن ، شرط لازم و کافی برای کامل بودنِ مجموعهی چند جملهایها در CØ است. این نتیجه پاسخ کامل مسألهی برنشتاین را بدست داد. آخیئزر در مجموعهی کارهای دیگر بر سر مسألهی زیر تحقیق کرد: از میان همهی توابع تام با درجهی متناهی و دارای مقادیر یا مشتقهای معلوم در مجموعهای متناهی از نقاط معینی در صفحهی مختلط، حداقل انحراف از تابع تام صفر را پیدا کنید. آخیئزر همچنین تعمیمی از نامساوی برنشتاین برای مشتق تابع تامی با درجهی متناهی بدست آورد. بعداً او و ب. یا. لِوین این نتایج را به دستهی مهمی از توابع چند مقداری تعمیم دادند. در 1340 / 1961 کتاب مهم دیگر او به نام Classiacl Moment Problem («مسألهی کلاسیک لنگر») انتشار یافت. در همان زمان آخیئزر بر سر مسائلی کار میکرد که با «قیاسهای پیوسته» (continual analogues)ی مسألهی کلاسیک لنگر ارتباط داشتند. او اثری از مارک کاک در مورد دترمینانهای فردهوْلِم وینر – هوپف با هستهی اِرمیتی را نیز بسط بیشتری داد.
، شرط لازم و کافی برای کامل بودنِ مجموعهی چند جملهایها در CØ است. این نتیجه پاسخ کامل مسألهی برنشتاین را بدست داد. آخیئزر در مجموعهی کارهای دیگر بر سر مسألهی زیر تحقیق کرد: از میان همهی توابع تام با درجهی متناهی و دارای مقادیر یا مشتقهای معلوم در مجموعهای متناهی از نقاط معینی در صفحهی مختلط، حداقل انحراف از تابع تام صفر را پیدا کنید. آخیئزر همچنین تعمیمی از نامساوی برنشتاین برای مشتق تابع تامی با درجهی متناهی بدست آورد. بعداً او و ب. یا. لِوین این نتایج را به دستهی مهمی از توابع چند مقداری تعمیم دادند. در 1340 / 1961 کتاب مهم دیگر او به نام Classiacl Moment Problem («مسألهی کلاسیک لنگر») انتشار یافت. در همان زمان آخیئزر بر سر مسائلی کار میکرد که با «قیاسهای پیوسته» (continual analogues)ی مسألهی کلاسیک لنگر ارتباط داشتند. او اثری از مارک کاک در مورد دترمینانهای فردهوْلِم وینر – هوپف با هستهی اِرمیتی را نیز بسط بیشتری داد.
آخیئزر دربارهی چند جملهایهای متعامد نسبت به یک تابع وزن بر روی مجموعهای از کمانهای دایره یا مجموعهای از بازههای محور حقیقی بررسی کرد؛ سپس این روشها را در مسائل وارون در تحلیل طیف بکار بست. فرض کنید
 عملگر استورم – لیوویل باشد که در آن q(x) تابع پیوستهی حقیقی و h مقدار ثابت حقیقی است. فرض میکنیم که طیف L به تعداد g شکاف داشته باشد. آخیئزر یک سطح اَبَر بیضوی ریمانی از گونهی g وابسته به عملگر L ساخت و آن را بررسی کرد؛ E(λ;x)، تابع متناظر بلوْخ، روی این سطح نسبت به λ تک مقدار است. {P1(x),…,Pg(x)} مجموعهی صفرهای آن نقش مهمی دارد: ب.آ. دوبروْوین بعداً نشان داد که پوتانسیئل q(x) را میتوان به صورت صریح به کمک توابع {P1(x),…,Pg(x)} بیان کرد. این نتایج در پیوست ویرایش سومِ Theory of Operators in Hilbert Space («نظریهی عملگرها در فضای هیلبرت») عرضه شدهاند. س. پ. نوْویکوف، ب. ا. دوبرووین، و مؤخرتر از آنها و.آ. مارچنکو، با استفاده از نتایج فوق راهحلهائی کارآمد و به صورت صریح برای دستههای قابل توجهی از معادلات دیفرانسیئل جزئی غیرخطی از نوع کورتوِخ – دِ وِریس یافتند.
عملگر استورم – لیوویل باشد که در آن q(x) تابع پیوستهی حقیقی و h مقدار ثابت حقیقی است. فرض میکنیم که طیف L به تعداد g شکاف داشته باشد. آخیئزر یک سطح اَبَر بیضوی ریمانی از گونهی g وابسته به عملگر L ساخت و آن را بررسی کرد؛ E(λ;x)، تابع متناظر بلوْخ، روی این سطح نسبت به λ تک مقدار است. {P1(x),…,Pg(x)} مجموعهی صفرهای آن نقش مهمی دارد: ب.آ. دوبروْوین بعداً نشان داد که پوتانسیئل q(x) را میتوان به صورت صریح به کمک توابع {P1(x),…,Pg(x)} بیان کرد. این نتایج در پیوست ویرایش سومِ Theory of Operators in Hilbert Space («نظریهی عملگرها در فضای هیلبرت») عرضه شدهاند. س. پ. نوْویکوف، ب. ا. دوبرووین، و مؤخرتر از آنها و.آ. مارچنکو، با استفاده از نتایج فوق راهحلهائی کارآمد و به صورت صریح برای دستههای قابل توجهی از معادلات دیفرانسیئل جزئی غیرخطی از نوع کورتوِخ – دِ وِریس یافتند.
دوم. خواندنیهای فرعی. «Naum Il"ich Akhiezer»، از م. برزانسکی، آ.ن. کلماگورف، م.گ. کرین، ب. یا. لوین، ب.م. لویتان، و و.آ.مارچنکو (به مناسبت هفتادمین سال تولد آخیئزر)، در UMN، 26، شمارهی 6 (1971)، 257-261؛ «Naum Il"ich Akhiezer»، از م.گ. کرین و ب. یا. لوین (به مناسبت شصتمین سال تولد آخیئزر)، همان، 16، شمارهی 4 (1961)، 223-232؛ و Nonlinear Equations and Operator Algebra، از و.آ. مارچنکو، ترجمهی و.ا. روبلینتسکی (دوْردرخت و باستن، 1988).
منبع مقاله :
کولستون گیلیپسی، چارلز؛ (1387)، زندگینامه علمی دانشوران، ترجمهی احمد آرام... [و دیگران]؛ زیرنظر احمد بیرشک، تهران: شرکت انتشارات علمی و فرهنگی، چاپ اول
Naum Il"ich Akhiezer
(ت. چریکوف، روسیهی سفید، 15 اسفند 1279 / 6 مارس 1901؛ و. خارکف، روسیه، 13 خرداد 1359 / 3 ژوئن 1980)، ریاضیات.
آخیئزر در سال 1302 از «مؤسسهی آموزش مردمی کییف» فارغالتحصیل شد، و بعد در دانشگاه کییف تحصیلات خود را برای اخذ درجهی نامزدی تحت نظارت د.آ. گراوی، که از نامداران رشتهی جبر بود، ادامه داد. او در پایاننامهی نامزدی خود، که به پژوهش در زمینهی آئرودینامیک اختصاص یافته بود، روشهای آنالیز مختلط را در مسائل آئرو دینامیک بکار بست. وی اولین کسی بود که فورمولی برای نگاشت همدیس دامنهی کثیرالاضلاعی دارای همبندی مضاعف به یک حلقه بدست آورد.
آخیئزر سخت درگیر مسائل نظریهی تقریب بود. در 1307 مسألهی دشواری را حل کرد: در میان همهی چند جملهایهای درجهی n، که ضرایب سه جمله از بالاترین درجات آن ثابت است، در بازهی معینی از محور حقیقی کمترین انحراف نسبت به چند جملهایِ صفر را پیدا کنید. آخیئزر نشان داد که راه حل این مسأله را میتوان به کمک توابع شوتکی بدست آورد. این نتیجه انگیزهی بحثی شد برای گسترش هرچه بیشتر نظریهی کلاسیک حداقل انحراف نسبت به چند جملهایهای صفر، که پ. ل. چیبیشوف، ن. زلتاریوف، و و.ا. مارکف عرضه کرده بودند. آخیئزر بعداً نشان داد که مسأله حداقل انحراف نسبت به چند جملهای صفر را در حالتی که k ضریب از ضرایب درجات بالای آن ثابتند میتوان به مسألهی یافتن حوزهای که همراه k برشهای قطعهای در امتداد محور حقیقی صفحهی مختلط باشد، و نیز به ساختنِ تابع گرینِ این حوزه، تقلیل داد.
آخیئزر در 1312 به خارکف نقفل مکان کرد، و در آنجا سالها سرپرست بخش آنالیز مختلط و رئیس «انجمن ریاضی خارکف» بود. در 1313 به عضویت مکاتبهای «فرهنگستان علوم اوکراین» انتخاب شد. در آن زمان آخیئزر و م. کرین شروع به بررسی مسألهی –L مؤمان کردند: مطلوب است
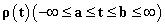 چگالیِ توزیع جرمی با موْمانهای معلوم که شرط اضافی
چگالیِ توزیع جرمی با موْمانهای معلوم که شرط اضافی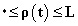 در آن صدق کند. خلاصهی پژوهشهای آنان در این زمینه در Some Questions in the Theory of Moments («پرسشهائی دربارهی نظریهی موْمانها»، 1933) مندرج است. آنان همچنین با چند جملهایهای مثلثاتی به مقدار دقیق یک ثابت در قضیهی دانم جکسن در مورد تقریب تابع متناوب پیبردند (این مقدار را ژان فاوار مستقلاً یافته بود).
در آن صدق کند. خلاصهی پژوهشهای آنان در این زمینه در Some Questions in the Theory of Moments («پرسشهائی دربارهی نظریهی موْمانها»، 1933) مندرج است. آنان همچنین با چند جملهایهای مثلثاتی به مقدار دقیق یک ثابت در قضیهی دانم جکسن در مورد تقریب تابع متناوب پیبردند (این مقدار را ژان فاوار مستقلاً یافته بود).آخیئزر در جریان جنگ جهانی دوم در «مؤسسهی معدنکاوی آلماآتا» (1320-1322) و «مؤسسهی مهندسی نیروی مسکو» (1322-1326) کار میکرد. در 1326، یعنی سالی که کتاب او دربارهی نظریهی تقریب منتشر شد، به خارکف بازگشت. او در این کتاب عقاید جدید مربوط به آنالیز تابعی را با روشهای کلاسیک درآمیخت و نتایج کار خودش را عرضه کرد. در 1328 جایزهی چیبیسوف به مناسبت این کتاب به او اعطا شد.
الهامبخش پژوهشهای بیشتر در این زمینه س.ن. برنشتاین – یکی از بنیادگذاران نظریهی تقریب – بود، که در 1303 مسألهی زیر را فوْرمولبندی کرده بود: فرض کنید
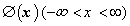 تابعی باشد که
تابعی باشد که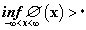 و
و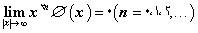 . حال فضای CØ از توابع پیوستهی ƒ(t) را چنان تعریف میکنیم که
. حال فضای CØ از توابع پیوستهی ƒ(t) را چنان تعریف میکنیم که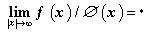 و فرض میکنیم که
و فرض میکنیم که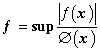
هنج واقع در CØ باشد. شرایط لازم و کافی برای Ø را چنان پیدا کنید که چند جملهایها مجموعهای چگال از CØ را تشکیل دهند. آخیئزر و ک. بابنکو، در کار مشترک خود بر سر این مسأله، MØ دستهی مهمی از چند جملهایهای P(x) را که در نامساوی
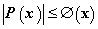 صدق میکردند بررسی نمودند و عبارت زیر را بدست آوردند
صدق میکردند بررسی نمودند و عبارت زیر را بدست آوردند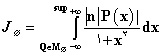
در 1332 آخیئزر و برنشتاین دریافتند که
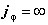 ، که در آن
، که در آن ، شرط لازم و کافی برای کامل بودنِ مجموعهی چند جملهایها در CØ است. این نتیجه پاسخ کامل مسألهی برنشتاین را بدست داد. آخیئزر در مجموعهی کارهای دیگر بر سر مسألهی زیر تحقیق کرد: از میان همهی توابع تام با درجهی متناهی و دارای مقادیر یا مشتقهای معلوم در مجموعهای متناهی از نقاط معینی در صفحهی مختلط، حداقل انحراف از تابع تام صفر را پیدا کنید. آخیئزر همچنین تعمیمی از نامساوی برنشتاین برای مشتق تابع تامی با درجهی متناهی بدست آورد. بعداً او و ب. یا. لِوین این نتایج را به دستهی مهمی از توابع چند مقداری تعمیم دادند. در 1340 / 1961 کتاب مهم دیگر او به نام Classiacl Moment Problem («مسألهی کلاسیک لنگر») انتشار یافت. در همان زمان آخیئزر بر سر مسائلی کار میکرد که با «قیاسهای پیوسته» (continual analogues)ی مسألهی کلاسیک لنگر ارتباط داشتند. او اثری از مارک کاک در مورد دترمینانهای فردهوْلِم وینر – هوپف با هستهی اِرمیتی را نیز بسط بیشتری داد.
، شرط لازم و کافی برای کامل بودنِ مجموعهی چند جملهایها در CØ است. این نتیجه پاسخ کامل مسألهی برنشتاین را بدست داد. آخیئزر در مجموعهی کارهای دیگر بر سر مسألهی زیر تحقیق کرد: از میان همهی توابع تام با درجهی متناهی و دارای مقادیر یا مشتقهای معلوم در مجموعهای متناهی از نقاط معینی در صفحهی مختلط، حداقل انحراف از تابع تام صفر را پیدا کنید. آخیئزر همچنین تعمیمی از نامساوی برنشتاین برای مشتق تابع تامی با درجهی متناهی بدست آورد. بعداً او و ب. یا. لِوین این نتایج را به دستهی مهمی از توابع چند مقداری تعمیم دادند. در 1340 / 1961 کتاب مهم دیگر او به نام Classiacl Moment Problem («مسألهی کلاسیک لنگر») انتشار یافت. در همان زمان آخیئزر بر سر مسائلی کار میکرد که با «قیاسهای پیوسته» (continual analogues)ی مسألهی کلاسیک لنگر ارتباط داشتند. او اثری از مارک کاک در مورد دترمینانهای فردهوْلِم وینر – هوپف با هستهی اِرمیتی را نیز بسط بیشتری داد.آخیئزر دربارهی چند جملهایهای متعامد نسبت به یک تابع وزن بر روی مجموعهای از کمانهای دایره یا مجموعهای از بازههای محور حقیقی بررسی کرد؛ سپس این روشها را در مسائل وارون در تحلیل طیف بکار بست. فرض کنید
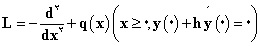
کتابشناسی
یکم. کارهای اصلی. آخیئزر 130 مقاله و 8 کتاب نوشت. برخی از کتابها بدین قرارند: Theory of Approximation، ترجمهی چارلز ج. هایمن (نیویورک، 1956)؛ Some Questions in the Theory of Moment، ترجمهی و. فلمینگ و د. پریل (پراویدنس، رو دآیلند، 1962)، با همکاری م. کرین؛ The Classical Moment Problem، ترجمهی ن. کِمِر (نیویورک، 1965)؛ و Theory of Operators in Hilbert Space، 2 جلد، ترجمهی ا.ر. دوْسن و ویراستهی و.ن. اوریت (باستن، 1981؛ چاپ سوم، 1987)، با همکاری ا.م.گلاسمن.دوم. خواندنیهای فرعی. «Naum Il"ich Akhiezer»، از م. برزانسکی، آ.ن. کلماگورف، م.گ. کرین، ب. یا. لوین، ب.م. لویتان، و و.آ.مارچنکو (به مناسبت هفتادمین سال تولد آخیئزر)، در UMN، 26، شمارهی 6 (1971)، 257-261؛ «Naum Il"ich Akhiezer»، از م.گ. کرین و ب. یا. لوین (به مناسبت شصتمین سال تولد آخیئزر)، همان، 16، شمارهی 4 (1961)، 223-232؛ و Nonlinear Equations and Operator Algebra، از و.آ. مارچنکو، ترجمهی و.ا. روبلینتسکی (دوْردرخت و باستن، 1988).
منبع مقاله :
کولستون گیلیپسی، چارلز؛ (1387)، زندگینامه علمی دانشوران، ترجمهی احمد آرام... [و دیگران]؛ زیرنظر احمد بیرشک، تهران: شرکت انتشارات علمی و فرهنگی، چاپ اول


.jpg)













