بَنوموسی

(تولد: بغداد، اواخر سده دوم و اوایل سده ی سوم/ آغاز سده ی نهم؛ وفات: بغداد، محمد که بزرگترین برادر بود در ربیع الاول یا دوم 259/ژانویه یا فوریه ی 873 درگذشت)

پدرشان موسی بن شاکِر در جوانی راهزن بود، اما بعد احکامی زبردستی شد. مرگ او به زمان خلافت مأمون (833-813 /218-198) فرا رسید و در آن زمان پسرانش خردسال بودند. مأمون به ذکاوت سه برادر پی برد و هر سه را در بیت الحکمه- که نخستین مؤسسه ی علمی در امپراتوری عباسیان و بسیار شبیه به فرهنگستانهای امروزی بود و مأمون آن را تأسیس کرده بود- به خدمت گماشت. دیری نکشید که بَنوموسی در ریاضیات و نجوم و علم حیل (مکانیک) سرآمد شدند و به صورت فعالترین عضوهای بیت الحکمه درآمدند. آنان به همراه ابوعبدالله محمد بن موسی خوارزمی پژوهشهای علمی بیت الحکمه را رهبری می کردند. خوارزمی بنیادگذار مکتب جبر اسلامی بود، در حالی که بَنوموسی به هندسه دلبستگی خاص داشتند و نیز رصد کواکب را رهبری می کردند، و مکتبی از مترجمان فراهم آوردند که نسخه های خطی علمی بسیاری را از یونانی به عربی می گرداندند، این ترجمه ها در گسترش علم بسی سودمند افتاد. برخی از کتابهای مهم یونانی اکنون فقط به صورت ترجمه ی عربی باقی مانده اند.
نامورترین مترجمان زمان به سرپرستی بَنوموسی کار می کردند. از آن جمله حنین بن اسحاق بود که معتبرترین مترجم کتابهای پزشکی شد، و ثابت بن قره دانشمند و مترجم سده ی سوم/نهم که، علاوه بر ترجمه ی کتابهای یونانی مانند اصول اقلیدس و سه مقاله از مخروطات آپولونیوس، آثار متعدد دیگری به وی منسوب است. بَنوموسی در زمره ی نخستین دانشمندان اسلامی بودند که به مطالعه ی کتابهای ریاضی یونانی پرداختند و مکتب اسلامی ریاضیات را بنیاد نهادند. آنان را می توان شاگردان ریاضیدانان یونانی خواند، اما از جهاتی که برای تطور برخی از مفاهیم ریاضی اهمیت بسیار دارد از ریاضیات متعارف یونانی منحرف گردیدند.
تشخیص نقشی که هر یک از سه برادر در کار مشترکشان ایفا کرده است دشوار است. اما به نظر می رسد که ابوجعفر محمد مهمترین آنان بوده است. محمد و حسن به هندسه دلبستگی خاص داشتند و احمد علاقه مند به مکانیک بود. محمد در نجوم هم کار می کرد.
مهمتر از همه ی کتابهای متعددی که به بَنوموسی منتسب است رساله ای است هندسی به نام کتاب معرفة مساحة الاشکال البسطیة و الکُریه (در اندازه گیری مساحت شکلهای مسطح و کروی). نسخه های خطی آن در اکسفورد و پاریس و برلین و استانبول و رامپور (هندوستان ) هست. یکی از نسخه های خطی به تحریر خواجه نصیر طوسی، ریاضیدان سده هفتم/سیزدهم به زبان عربی چاپ شده است. این کتاب در قرون میانه در جهان اسلام و اروپا شهرتی داشته است. بهترین گواه بر این مدعا ترجمه ی آن به زبان لاتینی در قرن ششم/ دوازدهم است به وسیله ی گرارد کرمونایی زیر عنوان Liber trium fratrum de geometria. نسخه های خطی این ترجمه در پاریس و مادرید و بازل و تورون و اکسفورد موجود است. منظور اصلی از این رساله، چنانکه در مقدمه ی آن آمده است، اثبات مهمترین قسمت روش یونانی تعیین مساحت و حجم است. این روش در رساله برای اندازه گیری دایره و کره به کار رفته است.
ارشمیدس در اندازه گیری دایره و در باب کره و استوانه مساحت دایره و سطح حجم کره را با روش ائودوکسوس، که بعداً «روش اِفنا» (یا تحلیل بردن) نامیده شد، به دست آورد. این روش بر اساس همان فکری استوار بود که شالوده ی نظریه ی حدها در ریاضیات جدید است. بعد از ارشمیدس این روش بی آنکه بهتر شود به کار می رفت. در واقع قرینه ای در دست نیست که بر آن دلالت کند تا قرن سوم/نهم درباره ی اندازه گیری مساحتها و حجمها کاری شده باشد.
بَنوموسی مساحت دایره را با روشی که با روش ارشمیدس تفاوت داشت، اما مبتنی بر اندیشه ی بینهایت کوچکهای او بود، حساب کردند. «روش اِفنا» را به کار بردند اما جزء اصلی آن را حذف کردند، بدین نحو که دنباله ای از چند ضلعیهای منتظم ضلعی (k=2,3,. . . ,n) در دایره محاط کردند و مساحتهای آنها را یافتند، آنگاه روش برهان خُلف را برای یافتن نتیجه ی مطلوب به کار بردند. اما از مراعات شرط حدی خودداری کردند؛ یعنی مساحت این گونه چند ضلعی را وقتی که kپیدا نکردند. به جای آن از گزاره ای که اثباتش مراعات حد را در برداشت تبعیت نمودند. این گزاره قضیه ی شانزدهم از مقاله ی دوازدهم اصول بود.
بَنوموسی با استفاده از این قضیه ثابت کردند که: هر گاه دایره ای به محیط C و پاره خطی به طول L داشته باشیم، و هر گاهLC ، آنگاه می توانیم در دایره چند ضلعی منتظمی به محیط (n عده ی ضلعها) محاط کنیم به نحوی که . و این بدین معنی است که می توانیم عدد صحیحی مانند N پیدا کنیم چنان که به ازای هر n > N، . در جزء دوم این گزاره بَنوموسی ثابت کردند که هر گاه L>C، آنگاه می توانیم چند ضعلی منتظمی به محیط بر دایره محیط کنیم به قسمی که . پس از این کار به آسانی می توان اثبات کرد که ( که در آن A مساحت و r شعاع دایره است).
باید خاطرنشان کرد که بَنوموسی مساحتها و حجمها را مساوی با حاصل ضربهای مقادیری تعریف کردند، حال آنکه یونانیان آنها را به وسیله ی مقایسه با مساحتها و حجمهای دیگری بیان می کردند. مثلاً ارشمیدس تعریف کرده بود که حجم کره چهار برابر حجم مخروطی است که ارتفاعش مساوی شعاع کره و قاعده اش مساوی با دایره ی عظیمه ی کره باشد. بَنوموسی به دست آوردند که حجم کره مساوی حاصل ضرب شعاع کره است در یک سوم سطح آن. به بیان دیگر، آنان برای تعیین مقدارهای هندسی از اعمال حسابی استفاده کردند. این خودگام مهمی بود برای گسترش دادن دستگاه اعداد، به طوری که علاوه بر عددهای صحیح عددهای گویا و گنگ را هم در بربگیرد. بَنوموسی در قضیه ی ششم روش ارشمیدس را برای تعیین تقریبی مقدار به اثبات رسانیدند. ارشمیدس با محاط کردن و محیط کردن 96 ضلعی منتظم در دایره و بر آن، ثابت کرده بود که باید بین مقدارهای و واقع باشد. بَنوموسی گفته اند که این روش را می توان ادامه داد تا به حدود مقدار
نزدیکتر شد. یعنی (که محیط چند ضلعی منتظم محیطی و محاطی است).
بَنوموسی، مانند ارشمیدس، تعیین کردند که مساحت سطح کره چهار برابر مساحت دایره ی عظیمه ی آن است، اما اثباتهایشان متفاوت بود. روش ارشمیدس هم ارز است با محاسبه ی انتگرال معین

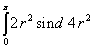
که در آن r شعاع کره است. برای اثبات بَنو موسی چنین نمی توان گفت، زیرا که آنان فقط مجموعی متناهی از رشته ی سینوسها را حساب کردند و ثابت نمودند که

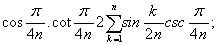
 اما این دستور را تا شرط حدی بسط ندادند. به جای آن از واقعیت ذیل، بی اثبات آن، استفاده کردند: هر دو کره ی هم مرکز را که در نظر بگیریم می توانیم در کره ی بزرگتر حجمی محاط کنیم که از دوران چند ضعلی منتظمی حول قطری از کره که بر دو رأس آن بگذرد به وجود آمده باشد، به قسمی که هیچ یک از وجوه این حجم بر کره ی داخلی مماس نباشد یا آن را قطع نکند. این موضوع را اقلیدس در قضیه ی هفدهم از مقاله ی دوازدهم اصول ثابت کرده بود. بَنو موسی حجم این چند وجهی را حساب کردند. آنگاه با استفاده از قضیه ی اقلیدس و برهان خُلف ثابت کردند که A=4C( که در آن A مساحت سطح کره و C مساحت دایره عظیمه ی آن است).
در رساله علاوه بر اندازه گیری دایره و کره سه مسئله ی متعارف یونانی حل شده بود:
بَنو موسی در گزاره ی هفتم رساله این قضیه را اثبات کردند که هر گاه aوbوc سه ضلعی مثلثی و A مساحت آن و 2/(a+b+c)p= باشد، آنگاه

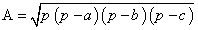
این قضیه را غالباً قضیه ی هِرون می گویند زیرا که اروپاییان اولین بار در Metrics هرون با آن برخورد کردند، اما این قضیه در کتاب گمشده ای از ارشمیدس، که اعراب بر آن وقوف داشتند، وجود داشته است. طریقه اثبات بَنو موسی با روش اثبات هرون فرق دارد.
تعیین دو واسطه ی هندسی. مسأله عبارت است از تعیین دو مقدار مجهول X و Y از روی دستورهای ، وقتی که a وb معلوم باشند. این مسأله را نخستین بار آرخوتاس(1) حل کرده بود. بَنوموسی این راه حل را هم نقل کرده اند، اما گفته اند که آن را از رساله ای هندسی اثر منلائوس به عاریت گرفته اند. آرخوتاس x وy را از تقاطع سه سطح منحنی به دست آورده بود: استوانه ی قائم و مخروط قائم و چنبره . هر گاه مختصات نقطه ی تقاطع این سه سطح منحنی باشند واضح است که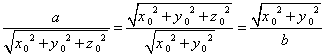

پس دو واسطه ی هندی مطلوب بین aو b اند. بَنوموسی برای حل این مسئله روش عملی به وسیله ی اسبابی که با چند خط کش به هم لولا شده بود ارائه کردند. این اسباب خیلی شبیه است به اسبابی که افلاطون به همین منظور طراحی کرده بود.
3. تثلیث زاویه. راه حل آنان برای این مسأله، مانند همه ی راه حل هایی که پیش از آن ارائه شده بود، سینماتیکی است.
بدین ترتیب آنچه در رساله ی بَنوموسی آمده است در حقیقت در محدوده معرفت هندسی قدیم است. با وجود این، این رساله صرفاً عرضه کردن کارهای هندسی یونانی نیست زیرا که مشتمل است بر اثباتهای تازه ای برای قضایای عمده ی اندازه گیری دایره و کره. بَنو موسی که کارهای ریاضیدانان یونان را خوانده بودند بسیاری از روشهای آنان را جذب کردند، اما در کاربرد روش یونانی بینهایت کوچک یعنی «روش افنا» رفتن به مرحله ی حد را کنار گذاشتند.
در سده های چهارم / دهم و پنجم/ یازدهم تعدادی از کتابهای ریاضی عربی درباره ی اندازه گیری شکلها از رساله ی کتاب معرفة الاشکال البسیطة و الکریة بَنو موسی اثر پذیرفتند. مهمترین این کتابها عبارت بودند از کتاب فی مساحة قطع المخروط الذی یسمی المکافیء (در تعیین مساحت مقطع مخروطی به نام سهمی) و مقالة فی مساحة المجسمات المکافیة (در اندازه گیری اجسام سهموی) از ثابت بن قره و کتابهای در اندازه گیری اجسام سهموی و در اندازه گیری کره از ابن هیثم. رساله ی بَنوموسی در قرون وسطا نقش بزرگی در نشر سنن اقلیدسی و ارشمیدسی در کشورهای اسلامی و در اروپا ایفا کرد. نفوذ آن در میان دانشمندان اروپایی قرون میانه را می توان به آسانی در Practica geometrica ی لئوناردو فیبوناتچی دید. در این کتاب چند قضیه از بَنوموسی می بینیم که در کتابهای یونانی نبوده است -مثلاً قضیه ای که می گوید که مقطع مخروط قائم با صفحه ای موازی قاعده، دایره است.
علاوه بر کتاب معرفة مساحة الاشکال البسیطة و الکریة تعدادی آثار دیگر به بَنوموسی منتسب است که یا به اندازه ی کافی و یا مطلقاً مورد مطالعه قرار نگرفته است. فهرستی از مهمترین این آثار در اینجا می آید:
1. مقدمات کتاب مخروطات، که تحریری است از مخروطات آپولونیوس که هلال حمصی (مقاله های اول تا چهارم) و ثابت بن قره (مقاله های پنجم تا هفتم) آن را به عربی ترجمه کرده بودند. این تحریر احتمالاً به وسیله ی محمد صورت پذیرفته بود. نسخه های خطی آن در اکسفورد و استانبول و لیدن هست.
2. کتاب الشکل المدور المستطیل (کتاب دایره ی کشیده). تصور می رود که این رساله، که حسن آن را نوشته است، بر اساس «ترسیم بیضی بوسیله ی باغبان»، یعنی رسم بیضی به کمک نخی که به دو کانون آن بسته شده باشد، تنظیم شده باشد.
3. قَرَسطون، رساله ای است درباره ی نظریه ی توزین و وسایل این کار.
4. در ابزارهای مکانیکی یا در علم حِیَل [حیل بَنو موسی]. این رساله را، که درباره ی ابزارهای با هوای فشرده است، احمد نوشته بوده است. نسخه های خطی آن در برلین و واتیکان مضبوط است.
5. کتاب در وصف اسبابی که خود به خود صدا می دهد. این اثر درباره ی نظریه ی موسیقی است و نسخه ای خطی از آن در بیروت هست.
بعضی از این کتابها شایسته ی آن است که به دقت مورد مطالعه قرار گیرد، بخصوص قرسطون و در ابزارهای مکانیکی.

پی نوشت ها :

1- Archytas.

کتابشناسی:
الف) آثار اصلی
از کتاب معرفة مساحة الاشکال البسیطة و الکریة، که کتاب عمده ی بَنوموسی است، دو چاپ موجود است، یکی در رسائل الطوسی، 2(حیدرآباد، 1940)، و دیگری
Liber trium fratrum de geometria, M. Curtze, ed. , in Nova acta Academiae Caesareae Leopoldino Carolinae germanicae naturae curiosorum, 49(1885).
ب) منابع فرعی
کارهای علمی بَنو موسی در آثار زیر مورد بحث قرار گرفته است:
Marshall Clagett, Archimedes in the Middle Ages, I(Madison, Wis. , 1964); M. Steinschneider, " Die Sohne des Musa ben Sckakir, " in Bibliotheca mathematica (Leipzig, 1887), pp. 44-48, 71-75; H. Suter , " Mathematiker und Astronomen der Araber und ihre Werke, " in Abhandlungen zur Geschichte der Mathematik (Leipzig, 1900), and "Die Geometria der Sohne des Musa b. Shakir, " in Bibliotheca mathematica, 3(1902), 259-272.
در منابع زیر هم می توان اطلاعاتی درباره ی زندگی و آثار بَنو موسی یافت:
C. Brockelmann, Geschichte der arabischen Litteratur, I(Leiden, 1939), p. 382 of Supp. I; G. Sarton, Introduction to the History of Science, I, 545-546, 560:
ابن ندیم، الفهرست، ویراسته ی گ. فلوگل (چاپ جدید، بیروت، 1964) 271، I؛ 127-126، II، ابن القفطی، تاریخ الحکما، ویراسته ی یولیوس لیپرت (لایپزیگ، 1903)؛ صص 443-441، 316-315. همچنین رجوع کنید به اثر زیر که حاوی بحث مختصری است درباره کتاب بَنوموسی در علم حیل:
E. Wiedemann, " Zur Mechanik und Technik bei der Arabern, " in Sitzungsberichte der Physikalisch-medizinischen Sozietat in Erlangen , 38(1906), esp. 6-8.
منبع مقاله :
گیلسپی، چارلز کولستون؛ (1389)، زندگینامه‌ی علمی دانشمندان اسلامی (جلد نخست)، ترجمه‌ی جمعی از مترجمان، تهران، شرکت انتشارات علمی و فرهنگی، چاپ چهارم