مسیر جاری :
 آمار و ریاضیات
آمار و ریاضیات
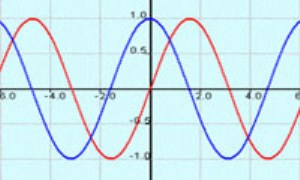
تابع
تعریف 1. تابع مجموعه ای از جفت های مرتب است که عنصرهای نخستین آن ها همه متفاوتند. تعریف 2. وقتی یک مقدار یک متغیر به متغیری دیگر وابسته باشد، اولی را تابع دومی می نامند.
 آمار و ریاضیات
آمار و ریاضیات
کواترنیون ها
بردارها اشیائی اند که می توان آن ها را از جمله جمع و تفریق، و ضرب کرد؛ آن ها را می توان در اعداد حقیقی هم ضرب نمود. در هر حالت، نتیجه یک بردار دیگر است.
 آمار و ریاضیات
آمار و ریاضیات
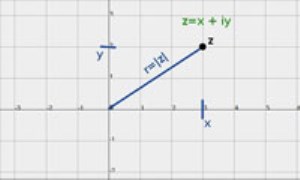
بزرگ ترین فاجعه جبری
از دیدگاه امروزی کاملاً مناسب تر است که از استفاده از کلمه ی «موهومی» اظهار تأسف شود و این امر «بزرگ ترین فاجعه جبری» نامیده شود؛ اما به قدری جا افتاده که ریاضیدانان از عهده ی الغای آن برنمی آیند. با این...
 آمار و ریاضیات
آمار و ریاضیات
پیمانه و همنهشت
(به پیمانه ی m ) x =y، بخوانید « x به پیمانه ی m با Y همنهشت است»، اگر عدد صحیح x -y بر عدد صحیح m تقسیم پذیر باشد. این مفهوم و نمادگذاری به وسیله ی کارل فریدریش گاوس در سال 1801، هنگامی که وی بیست و
 آمار و ریاضیات
آمار و ریاضیات
جبر بولی
به نظر می رسد که ایده ی وضع اصول موضوعه ای برای کار با علامت های مجرد (نه لزوماً اعداد) برای نخستین بار در انگلستان و حدوداً در زمان جورج بول (1815-1864) مطرح شده باشد. بول ایده های اصل خود را در 1847
 آمار و ریاضیات
آمار و ریاضیات
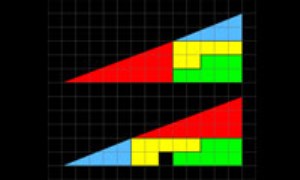
روش باستانی در دستان ریاضی دان مدرن
ریاضیدان ژاپنی، سکی کووا (1)(1683)، یک روش چینی باستان برای حل دستگاه معادلات خطی را نظام مند کرد که ضرایب آن به کمک چوب های محاسبه-میله های بامبو به شکل مربع هایی روی میزی قرار می گرفتند و موقعیت های
 آمار و ریاضیات
آمار و ریاضیات
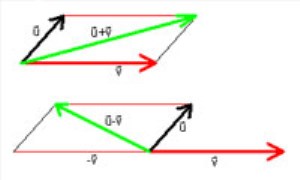
بردارها
ریشه های جبر برداری به مفهوم هندسی پاره خط های سودار در فضا باز می گردد. ترکیب نیروها به کمک قانون متوازی الاضلاع به ایده ی جمع بردارها انجامید. نمایش آن ها به عنوان مجموعه های مرتب از اعداد حقیقی تنها...
 آمار و ریاضیات
آمار و ریاضیات
فرمول کاردان
نخستین موارد ثبت شده ی علاقه ی انسان به معادله های درجه سوم، به تمدن بابلی باستان (حدود 1800-1600ق م) باز می گردد. در بین مواد ریاضی که جان به در برده اند، جدول هایی از ریشه های دوم و سوم نیز جدول هایی...
 آمار و ریاضیات
آمار و ریاضیات
روش هورنر
آنچه امروزه به نام روش هونر (1) (برای تقریب زدن ریشه های حقیقی یک معادله ی چند جمله ای با ضرایب عددی حقیقی) می شناسیم، به شکلی معادل پیش از آن که به وسیله ی چین چیوشائو (2) در سال 1247 منتشر شود، قرن ها
 آمار و ریاضیات
آمار و ریاضیات
خط کش محاسبه
ویلیام آوت رد (2) (1574-1660) اسقف شال فورد (3) و کشیش بخش آلبوری (4)، سوری(5)، یکی از تأثیرگذارترین ریاضیدانان زمان خود بود. به عنوان معلم، متقاضی بسیاری داشت، زیرا دانشگاه های آن زمان کمی آموزش در
