
مترجم: بهرام اسدیان
در ضمن یکی ازاساسی ترین استنتاج ها در خصوص شرطی ها وضع مقدّم است:
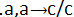 شرطی ها دربخش اعظمی ازاستدلال های ما نقشی محوری دارند. با وجود این کاربرد زیاد، شرطی ها عمیقاً مسئله انگیزند. منطق ازهمان اوائل عمرخود به بررسی آنها پرداخته است. به نقل ازکالیماخوس، یکی از شارحان دوران باستان، روزگاری بود که حتی کلاغ ها هم بر پشت بام ها درباره ی شرطی ها قارقار می کردند.
شرطی ها دربخش اعظمی ازاستدلال های ما نقشی محوری دارند. با وجود این کاربرد زیاد، شرطی ها عمیقاً مسئله انگیزند. منطق ازهمان اوائل عمرخود به بررسی آنها پرداخته است. به نقل ازکالیماخوس، یکی از شارحان دوران باستان، روزگاری بود که حتی کلاغ ها هم بر پشت بام ها درباره ی شرطی ها قارقار می کردند.ببینیم اصولاً چرا (یا لااقل یک دلیل پیدا کنیم که چرا) شرطی ها این قدر معضل خیزند. اگر بدانید که
 ، به نظر می رسد که می توانید
، به نظر می رسد که می توانید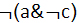 (چنین نیست که a و نه c) را از آن به دست آورید. فرض کنید کسی به شما می گوید اگر ازاتوبوس جا بمانید، دیرتان خواهد شد. ازاین حرف، شما می توانید نتیجه بگیرید که چنین نیست که من از اتوبوس جا بمانم و دیرم نشود. عکس ماجرا هم صادق است: اگر بدانید
(چنین نیست که a و نه c) را از آن به دست آورید. فرض کنید کسی به شما می گوید اگر ازاتوبوس جا بمانید، دیرتان خواهد شد. ازاین حرف، شما می توانید نتیجه بگیرید که چنین نیست که من از اتوبوس جا بمانم و دیرم نشود. عکس ماجرا هم صادق است: اگر بدانید  به نظر می رسد که حق دارید
به نظر می رسد که حق دارید را از آن به دست آورید. فرض کنید کسی به شما بگوید که اگر پول ندهید، در سینما فیلم نخواهید دید (چنین نیست که در سینما فیلم ببینی و پول نداده باشی). می توانید از حرف طرف این نتیجه را بگیرید که اگر من بخواهم در سینما فیلم ببینم، پس باید پول بدهم.
را از آن به دست آورید. فرض کنید کسی به شما بگوید که اگر پول ندهید، در سینما فیلم نخواهید دید (چنین نیست که در سینما فیلم ببینی و پول نداده باشی). می توانید از حرف طرف این نتیجه را بگیرید که اگر من بخواهم در سینما فیلم ببینم، پس باید پول بدهم.معمولاً
 را با
را با نمایش می دهند، و اسمش را هم شرطیِ مادی (3) می گذارند. پس آن طور که به نظر می آید، معنای
نمایش می دهند، و اسمش را هم شرطیِ مادی (3) می گذارند. پس آن طور که به نظر می آید، معنای و
و تا حدود بسیار زیادی شبیه هم است. با توجه به جدول های فصل 2 باید جدول ارزش صدقشان مثل هم باشد. نشان دهید که چرا جدول ارزش صدق شرطی این است: (تمرین ساده ای است).
تا حدود بسیار زیادی شبیه هم است. با توجه به جدول های فصل 2 باید جدول ارزش صدقشان مثل هم باشد. نشان دهید که چرا جدول ارزش صدق شرطی این است: (تمرین ساده ای است).
 هم صادق است. بعید است این حرف درست باشد. مثلاً، صادق است که کانبرا پایتخت فدرال استرالیا است، ولی شرطیِ «اگر کانبرا پایتخت فدرال استرالیا نباشد، کانبرا پایتخت فدرال استرالیا است» به نظر کاملاً کاذب می آید. جدول به ما می گوید اگر a کاذب باشد (ردیف سوم و چهارم)،
هم صادق است. بعید است این حرف درست باشد. مثلاً، صادق است که کانبرا پایتخت فدرال استرالیا است، ولی شرطیِ «اگر کانبرا پایتخت فدرال استرالیا نباشد، کانبرا پایتخت فدرال استرالیا است» به نظر کاملاً کاذب می آید. جدول به ما می گوید اگر a کاذب باشد (ردیف سوم و چهارم)، صادق است. ولی این هم بعید است درست باشد. شرطیِ «اگر سیدنی پایتخت فدرال استرالیا باشد، آنگاه بریزبین (4) پایتخت فدرال استرالیا است» نیز به وضوح کاذب است. کجای کار خراب است؟
صادق است. ولی این هم بعید است درست باشد. شرطیِ «اگر سیدنی پایتخت فدرال استرالیا باشد، آنگاه بریزبین (4) پایتخت فدرال استرالیا است» نیز به وضوح کاذب است. کجای کار خراب است؟این مثال ها نشان می دهند که→ تابع ارزش نیست: ارزش صدق
 بنابر ارزش صدق a و c تعیین نمی شود. هم «رم» در فرانسه است» کاذب است و هم «پکن در فرانسه است» ولی صادق است که:
بنابر ارزش صدق a و c تعیین نمی شود. هم «رم» در فرانسه است» کاذب است و هم «پکن در فرانسه است» ولی صادق است که:اگر ایتالیا بخشی از فرانسه باشد، رم در فرانسه است.
حال آن که جمله ی زیر کاذب است:
اگرایتالیا بخشی ازفرانسه باشد، پکن در فرانسه است.
واقعاً شرطی ها چگونه کار می کنند؟
برای پاسخ به این سؤال یک راه این است که ازدستگاه جهان های ممکنِ فصل قبل کمک بگیریم. دو شرطیِ آخر را در نظر بگیرید. در هرموقعیت ممکنی که ایتالیا با فرانسه ادغام شده باشد، رم در فرانسه خواهد بود. البته موقعیت های ممکنی هم هستند که در آن ها ایتالیا با فرانسه ادغام شده، ولی این به هیچ وجه تأثیری در چین ندارد. پس در این موقعیت پکن بازهم درفرانسه نیست. این حرف ها خبر از آن می دهند که شرطی a→c در موقعیت s صادق است اگر و تنها اگر c در هر یک از موقعیت های ممکن مرتبط با s، که a در آن صادق است، صادق باشد؛ و درموقعیت s کاذب است اگر c درفلان موقعیت ممکن مرتبط با s، که در a در آن صادق است، کاذب باشد.
از این طریق می توانیم توضیحی پذیرفتنی و معقول از →به دست دهیم.
مثلا می توانیم بگوییم چرا وضع مقدّم دست کم بنابر یک فرض معتبر است.و آن فرض این است که خود s یکی از موقعیت های مرتبط با s باشد. این حرف معقولی به نظر می آید: هرچیزی که به نحو بالفعل در s صادق است [یا در موقعیت فعلی s صادق است] حتماً ممکن است. فرض کنید a و
 در موقعیت s صادق باشند. دراین صورت، c در همه ی موقعیت های مرتبط با s، که a در آن ها صادق باشد، صادق است. ولی s خودش یکی از آن موقعیت هاست. و a در آن صادق است. پس c نیز صادق است.
در موقعیت s صادق باشند. دراین صورت، c در همه ی موقعیت های مرتبط با s، که a در آن ها صادق باشد، صادق است. ولی s خودش یکی از آن موقعیت هاست. و a در آن صادق است. پس c نیز صادق است.برگردیم به برهانی که با آن شروع کردیم. حالا می توانیم بفهمیم کجای کار خراب است. استنتاجی که برهان بر آن سوار است این است:

که معتبر نیست. مثلاً، اگر a در موقعیت s کاذب باشد، همین برای احراز صدق مقدمه درک کافی است. ولی این حرف چیزی دراین خصوص نمی گوید که a و c چگونه در موقعیت های ممکن مرتبط با s رفتار می کنند. کاملاً ممکن است که در یکی از این موقعیت ها، مثلاً s'،a صادق باشد و c کاذب؛ مثل این موقعیت:

می بینیم که در این جا در a صادق نیست.
در a صادق نیست.
وضع آن یکی مثال چه می شود؟ (کسی به شما می گوید اگر پول ندهید درسینما فیلم نخواهید دید). آیا استنتاج بالا دراین مورد معتبربه نظر نمی رسد؟ فرض کنید شما می دانید که بدون پرداخت پول درسینما فیلم نخواهید دید:
 آیا دراین جا واقعاً حق دارید نتیجه بگیرید که «اگر می خواهید در سینما فیلم ببینید، پول بدهید»؟ یعنی:
آیا دراین جا واقعاً حق دارید نتیجه بگیرید که «اگر می خواهید در سینما فیلم ببینید، پول بدهید»؟ یعنی:
 نه لزوماً. فرض کنید شما به دیدن فیلم نمی روید حتی اگر بلیت های آن شب مجانی باشد (مثلاً آن شب قرار است تلویزیون برنامه ای پخش کند که دیدنش برای شما ازدیدن فیلم جذاب تر باشد).
نه لزوماً. فرض کنید شما به دیدن فیلم نمی روید حتی اگر بلیت های آن شب مجانی باشد (مثلاً آن شب قرار است تلویزیون برنامه ای پخش کند که دیدنش برای شما ازدیدن فیلم جذاب تر باشد).
در این صورت، شما می دانید صادق نیست که به سینما می روید
 و بنابراین، صادق نیست که می روید و پول نمی دهید:
و بنابراین، صادق نیست که می روید و پول نمی دهید:
 . آیا دراین جا حق دارید نتیجه بگیرید که اگر به سینما بروید، پول می دهید؟ قطعاً نه، چون ممکن است بلیت های آن شب مجانی باشد.
. آیا دراین جا حق دارید نتیجه بگیرید که اگر به سینما بروید، پول می دهید؟ قطعاً نه، چون ممکن است بلیت های آن شب مجانی باشد.
توجه به این نکته مهم است که وقتی شما ازصدق مقدمه آگاه می شوید، معمولاً عوامل دیگری نیز آن پشت ها در کارند. وقتی کسی به شما خبری مثل
 را می دهد، معمولا این خبر را براساس دانش خود ازصدق
را می دهد، معمولا این خبر را براساس دانش خود ازصدق
 نمی دهد (چون اگر این را بداند، هر چه درباره ی آن موقعیت به شما بگوید حرف تازه ای نخواهد بود). اگر این خبر را به شما بدهد، بر این اساس این خبر را به شما داده که میان g و m رابطه ای فرض کرده؛ و آن این که نمی شود g صادق باشد ولی m صادق نباشد- و این دقیقا همان چیزی است که برای صدق شرطی لازم است. پس وقتی شما از صدق مقدمه آگاه می شوید، معمولا حق دارید
نمی دهد (چون اگر این را بداند، هر چه درباره ی آن موقعیت به شما بگوید حرف تازه ای نخواهد بود). اگر این خبر را به شما بدهد، بر این اساس این خبر را به شما داده که میان g و m رابطه ای فرض کرده؛ و آن این که نمی شود g صادق باشد ولی m صادق نباشد- و این دقیقا همان چیزی است که برای صدق شرطی لازم است. پس وقتی شما از صدق مقدمه آگاه می شوید، معمولا حق دارید
 را استنتاج کنید، ولی نه از روی محتوای آنچه گفته شده، بلکه صرفاً از این واقعیت که آن چیز گفته شده.
را استنتاج کنید، ولی نه از روی محتوای آنچه گفته شده، بلکه صرفاً از این واقعیت که آن چیز گفته شده.
اما واقعیت این است که ما اغلب بی آن که فکر کنیم، این جور استنتاج ها را درست انجام می دهیم. مثلاً فرض کنید من ازکسی می پرسم که چگونه فلان دستور را به کامپیوترمی دهد، و اوهم می گوید:«کتاب راهنما دارم».
من هم نتیجه می گیرم که این کتاب راهنما درباره ی کار با کامپیوتر است.
ولی نتیجه ی من از روی آنچه طرف گفته حاصل نشده؛ حرف طرف نامربوط بود اگر آن کتاب کتاب راهنمای کار با کامپیوتر نبود؛ ومردم هم معمولاً حرف های مربوط می زنند نه نامربوط. به این ترتیب، من حق دارم نتیجه بگیرم که آن کتاب کتاب راهنمای کار با کامپیوتر است. این استنتاج استنتاجی قیاسی نیست. چون به هرحال، کاملاً ممکن است که طرف آن حرف را زده باشد ولی کتاب کتاب راهنمای کار با کامپیوتر نباشد. با این حال، استنتاج استقرایی بسیارخوبی محسوب می شود. به این جوراستدلال ها معمولاً استلزام محاوره ای (5) می گویند.
این تبیین ازشرطی ها به نظر خوب می آید، دست کم تا این جای کار. ولی مسلماً مشکلاتی هم دارد. به این استنتاج ها توجه کنید:
اگر به رم بروی، درایتالیا خواهی بود.
اگر درایتالیا باشی در اروپا هستی.
بنابراین، اگر به رم بروی، در اروپا خواهی بود.
اگر x بزرگ تر از 10 باشد، آنگاه x بزرگ تر از 5 است.
بنابراین، اگر x بزرگ تر از 10 و کوچک تر از 100 باشد، آنگاه x بزرگ تر از 5 است.
این دو استنتاج به نظر کاملاً معتبر می آیند؛ بنابراین، می توان آن ها را به روش بالا توضیح داد. استنتاج اول را به این شکل می نویسیم:

 در s صادق است.
در s صادق است.استنتاج دوم را هم به این شکل می نویسیم:
2.

(a&b→c) در s صادق است.
تا این جا که همه چیز خوب و خوش پیش رفت. مشکل این جاست که استنتاج هایی هستند که دقیقاً همین شکل را دارند ولی نامعتبرند. فرض کنید انتخابات ریاست جمهوری فقط با دو نامزد برگزار می شود: اسمیت، رییس جمهور فعلی، و جونز، حالا به این استنتاج توجه کنید:
اگر اسمیت پیش از انتخابات بمیرد، جونز برنده خواهد شد. اگر جونز برنده ی انتخابات شود، اسمیت بازنشسته خواهد شد و حقوق بازنشستگی خواهد گرفت. بنابراین، اگر اسمیت پیش ازانتخابات بمیرد، بازنشسته خواهد شد وحقوق بازنشستگی خواهد گرفت.
شکل منطقی این استنتاج دقیقاً مثل 1 است. ولی مسلماً می توان موقعیتی را تصور کرد که در آن دو مقدمه صادق و نتیجه کاذب باشد- مگر این که موقعیت عجیب وغریبی را فرض کنیم که در آن دولت در زندگی پس از مرگ نیز به بازنشستگان حقوق بازنشستگی می دهد!
یا مثلاً این استنتاج را در مورد اسمیت درنظر بگیرید:
اگر اسمیت ازبالای پرتگاه مرتفعی پایین بپرد، خواهد مرد. بنابراین، اگر اسمیت از بالای پرتگاه مرتفعی پایین بپرد و چتر نجات داشته باشد، خواهد مرد.
شکل منطقی این استنتاج دقیقاً مثل 2 است. ولی این بار هم مسلماً می توان موقعیت هایی را تصور کرد که در آن ها مقدمه صادق و نتیجه کاذب باشد.
در مورد این وضعیت ها چه باید گفت؟ ترجیح می دهم خودتان فکر کنید. هر چند شرطی ها درقلب بیش تر استدلال های ماجا دارند، همچنان یکی ازبحث انگیزترین حوزه های منطق اند. اگر چه کلاغ ها دیگر درباره ی شرطی ها قارقار نمی کنند، بی شک منطقدان بر سر آن قیل و قال ها می کنند.
پی نوشت ها :
1-antecedent
2- conseguent
3- material conditional
4- Brisbane
5- conversational implicature
پریست، گراهام،(1386)، منطق، مترجم: بهرام اسدیان، تهران: نشر ماهی، چاپ سوم













.jpg)












