تألیف: حمید وثیق زاده انصاری
منبع :راسخون
منبع :راسخون
هیچ بخشی از ریاضیات گیج کنندهتر از هندسه نیست. دلیل اصلی آن تعداد بالای اصطلاحات هندسه است که دانش آموزان را گرفتار کرده است. متن زیر را بخوانید تا از با اهمیتترین اصطلاحات هندسی بهرهمند شوید.
 همهی بخشهای ریاضیات به یک اندازه سخت است ولی هندسه یکی از رعب آورترین آنها است! تعداد زیاد اصطلاحات گیج کنندهی هندسه و هم چنین تعاریف آن میتواند بدترین کابوس َشما را برایتان تداعی کند. این که فقط یک لیست کامل را بدون این که معنا و مفهوم آن را بفهمیم، حفظ کنیم، نمیتواند برای ما مفید باشد. بنا بر این, این لیست از اصطلاحات هندسه، به معنای شروع کار نیست. این لیست به معنای یک مرجع آماده برای کسانی است که قبلاً هندسه را مطالعه کردهاند. بیایید شروع کنیم.
همهی بخشهای ریاضیات به یک اندازه سخت است ولی هندسه یکی از رعب آورترین آنها است! تعداد زیاد اصطلاحات گیج کنندهی هندسه و هم چنین تعاریف آن میتواند بدترین کابوس َشما را برایتان تداعی کند. این که فقط یک لیست کامل را بدون این که معنا و مفهوم آن را بفهمیم، حفظ کنیم، نمیتواند برای ما مفید باشد. بنا بر این, این لیست از اصطلاحات هندسه، به معنای شروع کار نیست. این لیست به معنای یک مرجع آماده برای کسانی است که قبلاً هندسه را مطالعه کردهاند. بیایید شروع کنیم.
نقطه: یک نقطه به عنوان اساسیترین مفهوم و موجودیت هندسه میباشد که به عنوان یک موقعیت بی نهایت کوچک در فضا میتواند تعریف شود. یک نقطه با علامت (.) نشان داده می شود و با یک حرف بزرگ نام گذاری میشود.
خط: خط دومین شکل اساسی در هندسه است. تعاریف متعددی از یک خط وجود دارد . یکی از تعاریف این چنین میگوید که خط مجموعهای از تعداد بی نهایت زیاد از نقاط است که در تماس با یک دیگر قرار دارند، که در آنها تمام نقاط تنها در تماس با دو نقطه است (یعنی هر نقطه در تماس با دو نقطه مجاور خود است). تعریف دیگری میگوید که یک خط، یک نهاد بی نهایت طولانی هندسی، تنها دارای یک بعد است. به عنوان مثال طولی را در نظر بگیرید که شامل هیچ عرضی نمیشود. این فاصله کوتاهترین مسیر ممکن بین دو نقطه میباشد.
پاره خط: پاره خط بخشی از یک خط است که بین دو نقطهی مشخص قرار دارد، تنها تفاوت بین یک خط و یک پاره خط این است که یک پاره خط طول محدودی دارد و از دو طرف تا بی نهایت امتداد نیافته است.
نیم خط: نیم خط میتواند به صورت نصف یک خط نامیده شود. به این صورت که یک نقطهی مبدﺃ دارد و از طرف دیگر تا بی نهایت کشیده شده است.
خطوط موازی: خطوط یا پاره خطها ممکن است با هم موازی باشند. دو خطی که در یک صفحه قرار دارند را موازی نامیم اگر هرگز با هم تلاقی پیدا نکنند. دو پاره خط را در یک صفحه موازی نامیم اگر دو نقطه در هر نقطه از خط به فاصله مساوی از یک دیگر قرار داشته باشند.
زاویه: هنگامی که دو پاره خط هم دیگر را قطع کنند یا یک نقطهی پایان مشترکی با هم داشته باشند، شیب یک خط نسبت به دیگری، زاویه نامیده میشود که با مقیاس درجه اندازه گیری میشود.
زاویهی راست: اگر دو خط هم دیگر را تحت زاویهی 90 درجه قطع کنند، گفته میشود دو خط با هم زاویه راست تشکیل دادهاند.
زاویهی حاده: اگر زاویه تقاطع دو خط کمتر از 90 درجه باشد، آن زاویه به عنوان زاویهی حاده شناخته شده است.
زاویهی منفرجه: اگر زاویه تقاطع بیشتر از 90 درجه باشد, آن زاویه به عنوان زاویه منفرجه شناخته شده است.
دایره: دایره، مجموعهای از نقاط است که همهی آنها در یک فاصله مساوی از یک نقطهی واحد قرار دارند. این فاصله به عنوان شعاع شناخته شده است. فاصلهی بین دو نقطه از دایره که دور ترین فاصله را نسبت به هم دارند قطر شناخته شده که اندازهی آن دو برابر طول شعاع است. تعریف دیگری از دایره، یک چند ضلعی با تعداد اضلاع بی نهایت است .
محیط: طول مرز یا حاشیهی یک دایره به عنوان محیط شناخته شده است. مقدار آن بستگی به شعاع یا قطر دایره دارد و با استفاده از فرمول : شعاع×2×pi یا قطرpi× به دست میآید. (تقریباﱟpi=22/7=3.14).
مثلث: مثلث یک شکل بسته با سه ضلع است و از سه پاره خط تشکیل شده است. مثلث سه زاویه دارد که همیشه مجموع زوایایش 180 درجه است. یکی دیگر از خاصیتهای بسیار مهم یک مثلث این است که همیشه مجموع طول دو ضلع آن بیشتر از طول ضلع سوم آن است.
مثلث قائم الزاویه: مثلثی که یکی از زوایایش 90 درجه است در حالی که مجموع دو زاویهی دیگر 90 درجه هستند، مثلث قائم الزاویه نامیده میشود.
مثلث متساوی الساقین: مثلثی با دو ضلع دارای طولهای برابر را مثلث متساوی الساقین مینامند، زوایای رو به رو به این دو ضلع نیز با هم دیگر مساویاند.
مثلث متساوی الاضلاع: مثلثی با سه ضلع هم اندازه را مثلث متساوی الاضلاع مینامیم، هر سه زاویهی یک مثلث متساوی الاضلاع 60 درجه اندازه گیری میشود.
چهار ضلعی (چهار گوش): یک شکل بسته که دارای چهار ضلع است و مجموع زوایای ساخته شده توسط این اضلاع همواره 360 درجه است .
متوازی الاضلاع، مستطیل، مربع، لوزی، مثالهایی از چهار ضلعی هستند.
متوازی الاضلاع: یک چهار ضلعی است که اضلاع رو به رو به هم در آن موازی هستند. در یک متوازی الاضلاع زوایای رو به رو به هم موازی و زوایای مجاور مکمل هستند (یعنی مجموع آنها 180 درجه است).
لوزی: متوازی الاضلاعی با چهار ضلع هم اندازه است.
مستطیل: متوازی الاضلاعی با چهار زاویه راست (زاویه 90 درجه) یک مستطیل نامیده میشود.
مربع: مربع، مستطیلی است که هر چهار ضلع آن اندازهی برابری دارند. به عبارت دیگر یک متوازی الاضلاع که هم مستطیل است و هم لوزی، مربع نامیده میشود. (امیدواریم که منظورمان را گرفته باشید!)
در حدود صدها اصطلاح هندسی دیگر نیز وجود دارند که عمدتاﱢ مشتقات اصطلاحاتی هستند که در این مقاله در موردشان بحث شد. هنگامی که شما با این اصطلاحات اساسی آشنا شوید، دیگر درک اصطلاحات و معانی و تعاریف دیگر هندسه کار دشواری نخواهد بود.
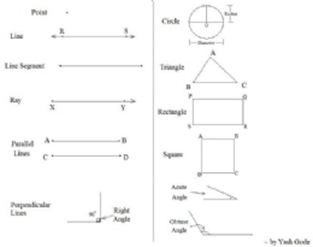
نقطه: یک نقطه به عنوان اساسیترین مفهوم و موجودیت هندسه میباشد که به عنوان یک موقعیت بی نهایت کوچک در فضا میتواند تعریف شود. یک نقطه با علامت (.) نشان داده می شود و با یک حرف بزرگ نام گذاری میشود.
خط: خط دومین شکل اساسی در هندسه است. تعاریف متعددی از یک خط وجود دارد . یکی از تعاریف این چنین میگوید که خط مجموعهای از تعداد بی نهایت زیاد از نقاط است که در تماس با یک دیگر قرار دارند، که در آنها تمام نقاط تنها در تماس با دو نقطه است (یعنی هر نقطه در تماس با دو نقطه مجاور خود است). تعریف دیگری میگوید که یک خط، یک نهاد بی نهایت طولانی هندسی، تنها دارای یک بعد است. به عنوان مثال طولی را در نظر بگیرید که شامل هیچ عرضی نمیشود. این فاصله کوتاهترین مسیر ممکن بین دو نقطه میباشد.
پاره خط: پاره خط بخشی از یک خط است که بین دو نقطهی مشخص قرار دارد، تنها تفاوت بین یک خط و یک پاره خط این است که یک پاره خط طول محدودی دارد و از دو طرف تا بی نهایت امتداد نیافته است.
نیم خط: نیم خط میتواند به صورت نصف یک خط نامیده شود. به این صورت که یک نقطهی مبدﺃ دارد و از طرف دیگر تا بی نهایت کشیده شده است.
خطوط موازی: خطوط یا پاره خطها ممکن است با هم موازی باشند. دو خطی که در یک صفحه قرار دارند را موازی نامیم اگر هرگز با هم تلاقی پیدا نکنند. دو پاره خط را در یک صفحه موازی نامیم اگر دو نقطه در هر نقطه از خط به فاصله مساوی از یک دیگر قرار داشته باشند.
زاویه: هنگامی که دو پاره خط هم دیگر را قطع کنند یا یک نقطهی پایان مشترکی با هم داشته باشند، شیب یک خط نسبت به دیگری، زاویه نامیده میشود که با مقیاس درجه اندازه گیری میشود.
زاویهی راست: اگر دو خط هم دیگر را تحت زاویهی 90 درجه قطع کنند، گفته میشود دو خط با هم زاویه راست تشکیل دادهاند.
زاویهی حاده: اگر زاویه تقاطع دو خط کمتر از 90 درجه باشد، آن زاویه به عنوان زاویهی حاده شناخته شده است.
زاویهی منفرجه: اگر زاویه تقاطع بیشتر از 90 درجه باشد, آن زاویه به عنوان زاویه منفرجه شناخته شده است.
دایره: دایره، مجموعهای از نقاط است که همهی آنها در یک فاصله مساوی از یک نقطهی واحد قرار دارند. این فاصله به عنوان شعاع شناخته شده است. فاصلهی بین دو نقطه از دایره که دور ترین فاصله را نسبت به هم دارند قطر شناخته شده که اندازهی آن دو برابر طول شعاع است. تعریف دیگری از دایره، یک چند ضلعی با تعداد اضلاع بی نهایت است .
محیط: طول مرز یا حاشیهی یک دایره به عنوان محیط شناخته شده است. مقدار آن بستگی به شعاع یا قطر دایره دارد و با استفاده از فرمول : شعاع×2×pi یا قطرpi× به دست میآید. (تقریباﱟpi=22/7=3.14).
مثلث: مثلث یک شکل بسته با سه ضلع است و از سه پاره خط تشکیل شده است. مثلث سه زاویه دارد که همیشه مجموع زوایایش 180 درجه است. یکی دیگر از خاصیتهای بسیار مهم یک مثلث این است که همیشه مجموع طول دو ضلع آن بیشتر از طول ضلع سوم آن است.
مثلث قائم الزاویه: مثلثی که یکی از زوایایش 90 درجه است در حالی که مجموع دو زاویهی دیگر 90 درجه هستند، مثلث قائم الزاویه نامیده میشود.
مثلث متساوی الساقین: مثلثی با دو ضلع دارای طولهای برابر را مثلث متساوی الساقین مینامند، زوایای رو به رو به این دو ضلع نیز با هم دیگر مساویاند.
مثلث متساوی الاضلاع: مثلثی با سه ضلع هم اندازه را مثلث متساوی الاضلاع مینامیم، هر سه زاویهی یک مثلث متساوی الاضلاع 60 درجه اندازه گیری میشود.
چهار ضلعی (چهار گوش): یک شکل بسته که دارای چهار ضلع است و مجموع زوایای ساخته شده توسط این اضلاع همواره 360 درجه است .
متوازی الاضلاع، مستطیل، مربع، لوزی، مثالهایی از چهار ضلعی هستند.
متوازی الاضلاع: یک چهار ضلعی است که اضلاع رو به رو به هم در آن موازی هستند. در یک متوازی الاضلاع زوایای رو به رو به هم موازی و زوایای مجاور مکمل هستند (یعنی مجموع آنها 180 درجه است).
لوزی: متوازی الاضلاعی با چهار ضلع هم اندازه است.
مستطیل: متوازی الاضلاعی با چهار زاویه راست (زاویه 90 درجه) یک مستطیل نامیده میشود.
مربع: مربع، مستطیلی است که هر چهار ضلع آن اندازهی برابری دارند. به عبارت دیگر یک متوازی الاضلاع که هم مستطیل است و هم لوزی، مربع نامیده میشود. (امیدواریم که منظورمان را گرفته باشید!)
در حدود صدها اصطلاح هندسی دیگر نیز وجود دارند که عمدتاﱢ مشتقات اصطلاحاتی هستند که در این مقاله در موردشان بحث شد. هنگامی که شما با این اصطلاحات اساسی آشنا شوید، دیگر درک اصطلاحات و معانی و تعاریف دیگر هندسه کار دشواری نخواهد بود.


























