نویسنده: آیت‌الله محمد تقی مصباح یزدی
قبل از کشف عدد پی (
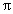)(1) دانشمندان زیادی تلاش کردند که فرمول محاسبه‌ی مساحت دایره را کشف کنند. یکی از این افراد، شخصی بنام «بروسُن»(2) بود. هدف او این بود که ثابت کند راهی برای تحصیل مساحتِ دایره وجود دارد. وی از استدلال هندسی استفاده کرده می‌گوید: ما دایره‌ای را در نظر می‌گیرم که در داخل و خارج آن هشت ضعلیهای منتظمی ترسیم شده است. فرض کنید سه تا هشت ضلعی در داخل دایره است و سه تا در خارج آن. این هشت ضلعی‌ها هر چه به مرکز دایره نزدیکتر باشند، کوچکتر می‌شوند و هر چه دورتر باشند بزرگتر می‌شوند.در تصویر فوق، بی‌نهایت هشت ضلعی را می‌توان فرض کرد چه در داخل دایره و چه در خارجِ آن. دو تا از این هشت ضلعی‌ها با دایره مماس می‌شوند: یکی از داخلِ دایره و یکی از خارجِ آن [چنانکه در شکل فوق آمده است]. البته اگر به جای هشت ضلعی، چهار ضلعی یا ده ضلعی یا .... فرض کنیم، باز هم فرقی نمی‌کند، فقط تفاوت در این است که نقطه‌های تماس دایره با دو چند ضلعی داخلی و خارجی، کم و زیاد می‌شود: اگر هشت ضلعی فرض کنیم، شکل داخلِ دایره در هشت گوشه (زاویه) با دایره مماس می‌شود و هشت ضلعیِ مماسِ بیرونی در هشت نقطه‌ی وسطِ هر ضلع با دایره مماس می‌شود (مانند شکل فوق). و اگر بیست ضلعی فرض کنیم، شکل داخلی در بیست زاویه و شکلِ خارجی در بیست نقطه‌ی وسط هر ضلعش با دایره مماس می‌شود. با دقت در تصویر فوق، روشن است که مساحتِ هشت ضلعیِ مماس خارجی بزرگتر از دایره، و مساحتِ هشت ضلعیِ مماس داخلی کوچکتر از دایره است. هشت ضلعیِ مماس خارجی، کوچکترین هشت ضلعیِ خارجی است و هشت ضلعیِ مماس داخلی، بزرگترین هشت ضلعیِ داخلی است. چون هشت ضلعیِ داخلی فقط در زوایای خود با دایره مماس است، لذا دایره در قسمتِ قوس‌های بین دو زاویه، از هشت ضلعی بزرگتر است. و امّا هشت ضلعیِ خارجی در وسطِ هر ضلعش با دایره مماس است و لذا در قسمت زوایایش از دایره بزرگتر است. حال بین این دو هشت ضلعیِ خارجی و داخلی، یک هشت ضلعیِ دیگر می‌توانیم فرض کنیم که مساحتش مساویِ مساحت دایره باشد که طبیعتاً این هشت ضلعی، از خارجی کوچکتر و از داخلی، بزرگتر است. این هشت ضلعیِ مساوی با دایره را می‌توان به مربع تبدیل کرد، زیرا اگر از هر زاویه‌ی هشت ضلعی، خطی به مرکز آن یعنی همان مرکزِ دایره رسم کنیم هشت تا مثلث به دست می‌آید و می‌دانیم هر مثلثی را می‌توان با مربّعی مساوی دانست. زیرا مساحت مثلث از ضربِ قاعده در نصفِ ارتفاع به دست می‌آید: مثلاً اگر قاعده‌ی مثلث، چهار باشد و ارتفاع آن هشت باشد، مساحت مثلث، معادلِ حاصلضربِ چهار در نصفِ هشت یعنی چهار خواهد بود و مساویِ شانزده می‌شود. حال اگر جذر شانزده را بگیریم، عدد چهار به دست می‌آید و چون مساحتِ مربع از ضربِ یک ضلع در خودش به دست می‌آید، اگر مربعی را با ضلعِ چهار فرض کنیم، مساحتش شانزده می‌شود که برابر است با مساحتِ مثلثِ مزبور.
مساحتِ مثلث ......
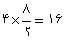
مجذورِ مساحتِ مثلث......
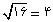
مساحت مربع ..... 16=4×4
ضلع مربع......
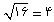
پس می‌توانیم یک هشت ضلعی را به هشت مثلث تبدیل کنیم و سپس هشت ضلعی را به هشت مربع و نهایتاً هشت مربع کوچک را به یک مربع بزرگ تبدیل کنیم. مثلاً اگر هشت مربع داشته باشیم که ضلعِ هر یک، دو باشد، می‌توانیم مساحتِ هر یک از مربع‌های کوچک یعنی عدد چهار را در هشت ضرب کنیم و حاصلضرب آن یعنی عدد (32) را به عنوان مساحتِ یک مربع بزرگ در نظر بگیریم. و مساحتِ این مربع بزرگ برابر است با مساحتِ آن دایره‌ای که با هشت ضلعیِ مورد بحث، مساوی است. از طرفی فرمول مساحت مربع این است که یک ضلع را در خودش ضرب کنیم و این مساحت، مساحتِ دایره هم خواهد بود و بنابراین می‌توان فرمولی برای محاسبه‌ی مساحت دایره ارائه کرد.
این بود آنچه بروسُن برای محاسبه‌ی مساحت دایره مطرح کرد.
- نقد سخن بروسُن
این برهان در صدد این است که امکان چنین چیزی را اثبات کند، و امّا چگونه می‌شود آن هشت ضلعی‌ای را که با دایره مساوی است، به دست آورد، محل تأمل است. بروسن خواسته از راه دو هشت ضلعیِ مماسِ داخلی و خارجی بگوید اگر هشت ضلعیِ وسطِ این دو را بگیریم، با دایره مساوی خواهد بود. حال سؤال این است که آیا آن برهان که می‌گوید امکان دارد مساحت دایره مساوی باشد با مربعی که مجذور ضلعِ آن، مساوی با مساحت دایره است، برای محاسبه‌ی مساحت دایره کافی است یا نه؟ سؤال دیگر این است که آیا از این راه می‌توان آن مربع را تعیین کرد یا نه؟ به نظر می‌رسد کلام و مقصود بروسُن کاملاً روشن نیست. اگر فقط بخواهد بگوید: امکان دارد مربعی مساوی دایره باشد، احتیاج به این همه مقدمات ندارد چون به هرحال مساحت هر دایره‌ای مساوی با عددی خواهد بود و آن عدد هم مساوی با مربعی خواهد بود که اگر جذر آن عدد را بگیریم، طول ضلع دایره می‌شود. ولی کلام در این است که آن مربع از چه راهی به دست می‌آید؟ و نیز بین آن دو هشت ضلعیِ داخلی و خارجی، عقلاً بی‌نهایت هشت ضلعی دیگر می‌توان فرض کرد. هم چنین به جای دو هشت ضلعی، دو مربع داخلی و خارجی هم فرض کرد، به گونه‌ای که مربعِ وسطِ این دو، مساوی با مساحت دایره باشد. امّا سخن در این است که آن هشت ضلعی یا مربعِ میانی که مساحتش با دایره مساوی است، کدام است و چگونه به دست می‌آید.ارسطو در این برهانِ بروسن مناقشاتی نموده و ابن‌سینا می‌فرماید مناقشات ارسطو، مجمل است. بعضی از شارحان، کلام ارسطو را تفسیر و تبیین کرده‌اند ولی ابن‌سینا بر کلام آنها نیز اشکال می‌کند و سپس خود تفسیر دیگری ارائه می‌دهد و در حقیقت، مناقشه‌ی دیگری در برهانِ مزبور وارد می‌کند. این مناقشه‌ی شیخ را، خواجه نصیر در اساس الاقتباس نقل و نقد می‌کند. و خلاصه این بحث، جدال شیرینی است که علاقمندانِ با حوصله، می‌توانند آن را دنبال کنند.
پی‌نوشت:
1. عدد پی [3/14] است که اگر در قطر دایره ضر شود محیط تقریبی آن به دست می‌آید. و اگر در مجذور شعاع دایره ضرب شود مساحت تقریبی دایره به دست می‌آید. به عبارت دیگر عدد پی(π) از تقسیم محیط بر دایره و یا تقسیم مساحت بر مجذور شعاع دایره به دست می‌آید. (غ).
2. Bryson ، در بعضی نسخ «بروشن» و در برخی «بروسن» آمده است. برای توضیح بیشتر در باره‌ی قیاسِ بروسن در تربیع دایره می‌توانید مراجعه کنید به «آنالوطیقای ثانی 75 ب 40 و سوفسطیفا 171 ب 16 ، 172/4 (غ).
مصباح یزدی، محمدتقی، (1384)، شرح برهان شفا (جلد اول و دوم)، تهران: انتشارات مؤسسه آموزشی و پژوهشی امام خمینی(رحمه‌الله)، چاپ اول
