
آقایان دکتر مهدی گلشنی و دکتر سعید سهراب پور به پاس مهربانیهایشان
چکیده
در این مقاله پس از بحث مختصری دربارهی موارد استعمال هفت ضلعی منتظم در هنرهای تزئینی اسلامی، علت ترسیم ناپذیری این شکل هندسی را به وسیله خط کش و پرگار شرح میدهیم؛ آنگاه دو راه حل تقریبی ترسیم این شکل را ارائه داده و برای آنها برهان هندسی میآوریم. یکی از این روشها متعلق به ابوالوفای بوزجانی ریاضیدان برجستهی ایرانی است که در کتاب تجارت او مورد بحث قرار گرفته است.کلیدواژهها:
هفت ضلعی منتظم، هنر اسلامی، ابوالوفای بوزجانی، ابوریحان بیرونی، ابوالجود بن لیث، روش هورنر.مقدمه
از جمله اشکال هندسی که در هنرهای تزئینی اسلامی و به ویژه هنر گره چینی به وفور به کار رفته و میرود، هفت ضلعی منتظم است. برای مثال این شکل را میتوان در گروههایی که زیر گنبدهای مساجد جامع اصفهان و جامع ساوه به کار رفته است مشاهده کرد.عکس این دو مکان را در زیر نشان دادهایم. (2)


آقای فرشته نژاد طرز تهیه این گره را که به « هفت و ده » معروف است به صورت زیر نشان داده است. (3)



بدیهی است که مبتکران این گرهها هم با هندسه و هم با هنر آشنائی داشتند و این شکلهای بدیع را به یاری ذوق هنری و نبوغ هندسی خود میآفریدند. اما به مروز زمان، یعنی هنگامی که این طرحها در دسترس صنعتگران قرار گرفت، این صنعتگران، طرحها و یا گرههای مزبور را تنها به یاری شهود تجربی خود بازآفرینی میکردند و در بیشتر موارد از مسائل هندسی آن آگاهی چندانی نداشتند. مثلاً آنها نمیدانستند که در این گره « ده و هفت » بحث از هفت ضلعی منتظمی است که ترسیم آن با « خط کش و پرگار » یعنی ساده ترین وسیله بنایان ممکن نیست، و برای آنکه این شکل را به صورت تقریبی و با استفاده از خط کش و پرگار رسم کنند باید به ترفندهای ریاضی متوسل شوند.
به راستی صنعتگران ایرانی، هفت ضلعی منتظم را چگونه رسم میکردند؟ ما پاسخ این سؤال را در بخش دوم این مقاله میدهیم.
1. اثبات ترسیم ناپذیری هفت ضلعی منتظم با خط کش و پرگار
رسم هفت ضلعی منتظم به معادله درجه سوم منجر میشود و بنابراین قابل رسم با خط کش و پرگار نمیباشد. زیرا هرگاه داشته باشیم و در صفحه z دایرهای به شعاع واحد رسم کنیم تقسیم این دایره به 7 قسمت
و در صفحه z دایرهای به شعاع واحد رسم کنیم تقسیم این دایره به 7 قسمت به حل معادله:
به حل معادله:

 است که آفیکس
است که آفیکس  است. این ریشه را با تقسیم معادله مزبور به
است. این ریشه را با تقسیم معادله مزبور به حذف میکنیم . از نظر هندسی این مسئله به این منجر میشود که نقطه شروع تقسیم دایره را به حساب نیاوریم. بنابراین معادله:
حذف میکنیم . از نظر هندسی این مسئله به این منجر میشود که نقطه شروع تقسیم دایره را به حساب نیاوریم. بنابراین معادله:

 تقسیم نماییم خواهیم داشت:
تقسیم نماییم خواهیم داشت:

(1)

 خواهیم داشت:
خواهیم داشت:(2)

 آفیکس
آفیکس  میباشد نیز میدانیم:
میباشد نیز میدانیم:

بنابراین هرگاه بتوانیم y را با خط کش و پرگار رسم کنیم آنگاه قادر خواهیم بود
 را نیز با همین آلات رسم نماییم.
را نیز با همین آلات رسم نماییم.اما رسم
 و در نتیجه رسم هفت ضلعی منتظم به حل معادلهی (2) بستگی دارد. از طرفی میدانیم که یک ساختمان هندسی هنگامی با خط کش و پرگار قابل رسم است که به معادلهی درجهی دوم منجر میشود، در حالی که معادلهی (2) درجهی سوم بوده و غیر قابل تحویل به معادله درجه دوم است. بنابراین هفت ضلعی منتظم با خط کش و پرگار غیر قابل رسم میباشد.
و در نتیجه رسم هفت ضلعی منتظم به حل معادلهی (2) بستگی دارد. از طرفی میدانیم که یک ساختمان هندسی هنگامی با خط کش و پرگار قابل رسم است که به معادلهی درجهی دوم منجر میشود، در حالی که معادلهی (2) درجهی سوم بوده و غیر قابل تحویل به معادله درجه دوم است. بنابراین هفت ضلعی منتظم با خط کش و پرگار غیر قابل رسم میباشد.
2. روش عملی ترسیم هفت ضلعی منتظم
به علت ترسیم ناپذیری هفت ضلعی منتظم با خط کش و پرگار ریاضیدانان برجسته اسلامی همچون حسن بن هیثم، ابوسهل کوهی و ابوسعید سجزی هر یک روشهایی را برای ترسیم هفت ضلعی منتظم ابداع کردند. (4) از آنجائی که این روشها فقط و فقط کاربرد ریاضی داشت و با استفاده از مقاطع مخروطی صورت میگرفت و انجام آنها از عهده صنعتگران که اغلب از معلومات ریاضی بهره چندانی نداشتند، خارج بود، هم ریاضیدانان و هم صنعتگران در پی یافتن روشهای سادهی دیگری برای ترسیم هفت ضلعی منتظم برآمدند. یکی از این روشها که در آثار صنعتگران آمده روشی است که ما از مبتکر آن آگاهی نداریم، روش دیگر روشی است که ظاهراً به وسیله ابوالوفای بوزجانی ابداع گردیده و در کتاب نجارت او آمده است. ما در زیر این دو روش را مورد بررسی قرار میدهیم.2. 1. روش متداول صنعتگران ایرانی
این روش را ما از کتاب گره چینی آقای زمرشیدی اقتباس کردهایم. (5)1. ابتدا دو محور افقی و عمودی رسم میکنیم. سپس به شعاع دلخواه دایرهای میزنیم و قطر (
 2. ) دایره را به هفت قسمت مساوی تقسیم میکنیم.
2. ) دایره را به هفت قسمت مساوی تقسیم میکنیم.2. از مرکز
 به شعاع جدید
به شعاع جدید  نیم دایرهی بزرگتری میزنیم تا محور افقی XX را در نقطهی
نیم دایرهی بزرگتری میزنیم تا محور افقی XX را در نقطهی قطع کند.
قطع کند.3. از نقطه
 به نقط تقسیم روی قطر
به نقط تقسیم روی قطر  خطوطی میکشیم تا از تقاطع این خطوط با دایره کوچک نقاط 5 و 6 و 7 به دست آید. به همین ترتیب نیز نقاط 1 و 2 و 3 را به دست میآوریم. آنگاه نقاط به دست آمده را به یکدیگر وصل میکنیم تا هفت ضلعی به وجود آید.
خطوطی میکشیم تا از تقاطع این خطوط با دایره کوچک نقاط 5 و 6 و 7 به دست آید. به همین ترتیب نیز نقاط 1 و 2 و 3 را به دست میآوریم. آنگاه نقاط به دست آمده را به یکدیگر وصل میکنیم تا هفت ضلعی به وجود آید.

برهان
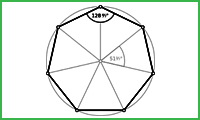
همانطوریکه در کتاب آقای زمرشیدی نیز آمده است صنعتگران ایرانی به طور کلی برای رسم هر یک از چند ضلعیهای منتظم به این شیوه عمل میکردند. ما نیز در مقالهای که پیش از این به چاپ رساندهایم از روش فوق برای رسم نه ضلعی منتظم (6) بهره برده و برهانی برای درستی این روش ارائه دادهایم. در این بخش میکوشیم که نه فقط برای هفت ضلعی بلکه برای چند ضلعیهائی که با این روش رسم میشوند برهانی ارائه دهیم. برای این منظور فرض میکنیم دایرهایکه قرار است هفت ضعلی منتظم در آن محاط شود، شعاعی برابر با واحد داشته باشد.هرگاه قطرهای ab و so این دایره را محورهای مختصات فرض نمائیم شکل زیر را خواهیم داشت. (7)

معادله پاره خط sc چنین است:
(1)

(2)

یعنی هرگاه مقدار M را از معادله (1) در معادله (2) قرار دهیم خواهیم داشت:

(3)

 نقطهی p بزرگترین جواب است. بنابراین باید جوابی را انتخاب کنیم که علامت + قبل از رادیکال داشته باشد. یعنی جواب مورد قبول عبارت است از:
نقطهی p بزرگترین جواب است. بنابراین باید جوابی را انتخاب کنیم که علامت + قبل از رادیکال داشته باشد. یعنی جواب مورد قبول عبارت است از:(4)


هرگاه این مقدار از x را در معادله (1) قرار دهیم عرض نقطه p نیز چنین به دست میآید:
(5)

 بنامیم، تانژانت این زاویه بعد از ساده کردن به صورت زیر نوشته میشود:
بنامیم، تانژانت این زاویه بعد از ساده کردن به صورت زیر نوشته میشود:


 را برای
را برای  حساب کرده و این مقدار تقریبی زاویههای n ضلعی مورد بحث را با مقدار حقیقی آنها یعنی:
حساب کرده و این مقدار تقریبی زاویههای n ضلعی مورد بحث را با مقدار حقیقی آنها یعنی: مقایسه کنیم.
مقایسه کنیم.ما مقادیر
 برای
برای  محاسبه کرده و در جدول زیر قرار میدهیم:
محاسبه کرده و در جدول زیر قرار میدهیم:

 خطای حاصل نیم درجه است. این خطا برای
خطای حاصل نیم درجه است. این خطا برای  از
از  درجه تجاوز نمیکند. بنابراین خطای این روش قابل چشم پوشی است و خلاصه هفت ضلعی حاصل از این روش را در عمل میتوان منتظم دانست.
درجه تجاوز نمیکند. بنابراین خطای این روش قابل چشم پوشی است و خلاصه هفت ضلعی حاصل از این روش را در عمل میتوان منتظم دانست.
2-2. روش تقریبی ابوالوفای بوزجانی
روشی که در کتاب نجارت، بوزجانی برای ترسیم هفت ضلعی منتظم ارائه شده اگر چه باز هم تقریبی است، ولی سادهتر از روش صنعتگران است. زیرا در این روش دیگر بر تقسیم قطر دایره به هفت قسمت مساوی که دقت فراوان میخواهد نیازی نیست.ما این روش را روش بوزجانی میگوئیم، زیرا آن را از کتاب هندسه عملی وی که همانا کتاب نجارت است اقتباس کردهایم. در حالی که ظاهراً مبتکر این روش هرون اسکندرانی بوده است. (8)
بوزجانی در این باره در کتاب مذکور چنین نوشته است:
چون خواهیم که بر خط « ا ب » مسبعی متساوی الاضلاع کنیم، خط « ب ج » مساوی خط « ا ب » بر استقامت اخراج کنیم و بر خط « ا ج » مثلث « ا د ج » متساوی الاضلاع بکشیم چنانکه گفتیم. پس برین مثلث دایرهای کنیم چنانچه در باب پنجم بعد از این بیان کنیم و درین دایره وتر « ا هـ » مساوی خط « ا ب » بکشیم و آن را [در نقطه ر] تنصیف کنیم و بر نقطه « ر » عمود « ر ح » بکشیم تا به دایره برسد. پس « ا ب » را بر نقطه « ط » تنصیف کنیم و عمود « ط ی » مساوی عمود « ر ح » بکشیم پس بر نقطههای « ا » ، « ب » ، «ی » دایره « ا ب » بکشیم چنانکه بعد ازین معلوم شود و در آن دایره قوسهای « ا ک » ، « ک ل » ، « ل ی » ، «ی م » « م ن » [ و ] « ن ب » باز کنیم هر یکی مساوی قوس « ا ب » و اوتار این قوسها بکشیم مسبع « ا ک ل ی م ن ب » حاصل آید متساوی الاضلاع برین صورت: (9)

برای ترسیم هفت ضلعی منتظم روی پاره خط مفروض AB نخست، مثلث متساوی الاضلاعی میسازیم که ضلع آن برابر با 2AB باشد. آنگاه دایره محیطی این مثلث را رسم میکنیم. در این دایره وتر AH را برابر AB رسم میکنیم AH برابر با ضلع هفت ضلعی منتظم خواهد بود. هرگاه شعاع دایره محیطی هفت ضلعی را واحد بگیریم خواهیم داشت:


برهان درستی این ترسیم
کافی است طول ضلع هفت ضلعی حاصل از روش بوزجانی را محاسبه کرده و آن را با مقدار حقیقی آن، که از فرمول به دست میآید مقایسه کنیم تا درجه دقت این روش را مشاهده نمائیم.
به دست میآید مقایسه کنیم تا درجه دقت این روش را مشاهده نمائیم.دایرهای به شعاع واحد را مطابق شکل زیر به هفت قسمت مساوی تقسیم کرده و نقاط تقسیم را به ترتیب E, K, J, D, C, B, A مینامیم.

دو مثلث قائم الزاویه DCL و DQC با هم متشابهاند در نتیجه داریم:




(1)










(5)


و با توجه به اینکه مقدار حقیقی طول ضلع هفت ضلعی منتظم محاط در دایره به شعاع واحد برابر است با:

3- تحلیل ابوالجود محمدبن لیث
روش فوق تقریبی است و ابوالوفا کاملاً به این امر واقف بوده است. این مسئله در میان سه مسئلهای که ابوریحان بیرونی از ریاضیدان معاصرش ابوالجود پرسیده و ابوالجود به این سوالات در رسالهای تحت عنوان جواب الشیخ الفاضل ابی الجود محمدبن اللیث ایده لله عما ساله عنه الاخ الفاضل ابوالریحان محمدبن احمد البیرونی پاسخ گفته موجود است. نسخهای از این رساله به شماره 168 در کتابخانهی دانشگاه لیدن نگاهداری میشود. پاسخهای مربوط به سؤالات اول و سوم را وپکه در ملحقات جبر و مقابله خیام مورد بررسی قرار داده است، (12) پاسخ سؤال دوم بیرونی که موضوع بحث ما است چنین عنوان دارد:ما البرهان علی استحالهی قول القائل ان وتر سبع کل دائره یساوی نصف وتر ثلها.
« اثبات اشتباه کسی که میگوید وتر هفتمین قسمت دایره مساوی با نصف وتر سومین قسمت آن است، چیست » .
این مسئله را آقای هوخندایک (13) از روی نسخه لیدن مورد بررسی قرار داده و متن عربی ابوالجود و ترجمه انگلیسی آن را نیز به چاپ رسانده است، آقای رشدی راشد (14) نیز همین مسئله را ضمن مسائل مورد بحث بیرونی در مقالهای به زبان فرانسه مورد تحلیل قرار داده است. ما با استفاده از مقاله هوخندایک، به بررسی این موضوع میپردازم.
ابوالجود برای اینکه اثبات کند هفت ضلعی حاصل از ترسیم فوق منتظم نیست به برهان خلف متوسل میشود. به این صورت که نخست یک مثلث متساوی الساقین محاط در یک دایره را رسم میکند که یکی از زاویههای آن برابر با
 است. آنگاه با استفاده از خواص این مثلث یک رابطه متری به دست میآورد بعد نیز ثابت میکند که هرگاه فرض مسئله را بپذیریم که عبارت است از
است. آنگاه با استفاده از خواص این مثلث یک رابطه متری به دست میآورد بعد نیز ثابت میکند که هرگاه فرض مسئله را بپذیریم که عبارت است از  این رابطه نمیتواند برقرار شود.
این رابطه نمیتواند برقرار شود.استدلال ابوالجود چنین است:
فرض میکنیم:
 نقطه G را طوری تعیین میکنیم که ABG متساوی الساقین باشد. پس:
نقطه G را طوری تعیین میکنیم که ABG متساوی الساقین باشد. پس: نقاط D و E را به ترتیب روی BG و AG طوری در نظر میگیریم که داشته باشیم:
نقاط D و E را به ترتیب روی BG و AG طوری در نظر میگیریم که داشته باشیم:

از تشابه دو مثلث قائم الزاویه EGT و AGZ نتیجه میشود:
 حال ابوالجود با فرض اینکه
حال ابوالجود با فرض اینکه  به محاسبات عددی روی میآورد.
به محاسبات عددی روی میآورد.فرض میکند AB=1 بنابراین با استفاده از فرض مسئله
 خواهد شد. اکنون با در دست داشتن این مقدار میتوانیم متوالیاً قطر دایره محیطی مثلث و نیز مقادیر عددی GTو GZ, AG را بدست آوریم.
خواهد شد. اکنون با در دست داشتن این مقدار میتوانیم متوالیاً قطر دایره محیطی مثلث و نیز مقادیر عددی GTو GZ, AG را بدست آوریم.

ابوالجود سپس با استفاده از این مقادیر نامساوی زیر را ثابت میکند:



ضمیمهی 1
روش روفینی و هورنر برای حل تقریبی معادلات درجه nاین روش که بیشتر به روش هورنر شهرت دارد مبتنی بر حدس نخستین ریشه مثبت معادله است و الگوریتمی ارائه میکند که بنابر آن، طی یک سلسله حدسهای دنباله دار، ارقام بعدی ریشههای مورد نظر یکی پس از دیگری به دست میآیند.
روش هورنر را به عنوان نمونه برای حل معادله درجه سوم زیر به کار میگیریم و در حین عمل، خود روش را نیز شرح میدهیم.
معادله
 را در نظر بگیرید، میخواهیم کوچکترین ریشه مثبت آن را به دست آوریم. از آنجا که اعداد 1 و 2 با قرار گرفتن در معادله، دو علامت مختلف به P(X) میدهند، پس ریشه مورد نظر بین 1 و 2 است.
را در نظر بگیرید، میخواهیم کوچکترین ریشه مثبت آن را به دست آوریم. از آنجا که اعداد 1 و 2 با قرار گرفتن در معادله، دو علامت مختلف به P(X) میدهند، پس ریشه مورد نظر بین 1 و 2 است.
جدول هورنر را برای ضرایب معادله فوق تشکیل میدهیم و به ازای
 ضرایب جدیدی به دست میآوریم: ( الگوریتم پر کردن جدول با دقت به علائم مشخص است: پیکانها علامت ضرب .t در خانه مبدأ و خطوط افقی سیاه علامت جمع است ).
ضرایب جدیدی به دست میآوریم: ( الگوریتم پر کردن جدول با دقت به علائم مشخص است: پیکانها علامت ضرب .t در خانه مبدأ و خطوط افقی سیاه علامت جمع است ).

ضرایب p (x)
برای بدست آوردن دومین رقم ریشه مورد نظر، معادله را با ضرایب جدید بازنویسی میکنیم . منتها در هر مرتبه، ضرایب را در یکی از توانهای 10 نیز ضرب میکنیم. معادله جدید چنین خواهد بود:

ضرب توانهای 10
 مطابق روش هورنر، با حدس زدن کوچک ترین ریشه معادله جدید که لزوماً 1 و 10 خواهد بود، دومین رقم از ریشه معادله اصلی را نیز به دست آوردهایم. در اینجا میبینیم ریشه معادله جدید بین 3 و 4 قرار گرفته است. بنابراین رقم 3 را یافتهایم و با فرض و قرار دادن ضرایب معادله جدید در جدول هورنر به یافتن رقمهای بعدی ادامه میدهیم و ارقام بعدی بدین ترتیب به دست میآیند:
مطابق روش هورنر، با حدس زدن کوچک ترین ریشه معادله جدید که لزوماً 1 و 10 خواهد بود، دومین رقم از ریشه معادله اصلی را نیز به دست آوردهایم. در اینجا میبینیم ریشه معادله جدید بین 3 و 4 قرار گرفته است. بنابراین رقم 3 را یافتهایم و با فرض و قرار دادن ضرایب معادله جدید در جدول هورنر به یافتن رقمهای بعدی ادامه میدهیم و ارقام بعدی بدین ترتیب به دست میآیند:X. =1.3819650
ضمیمهی 2
متن منقح تحلیل ابوالجود از روی چاپ هوخندایک
السؤال الثانی. ما البرهان علی استحالة قول القائل کن وتر سبع کل دائرة مساو لنصف وتر ثلثها.
الجواب لیکن ا ب نصف ضلع المثلث المتساوی الاضلاع الواقع فی دائرة ا ب ج و نخرج من نقطتی ا ب خطی ا ج ، ب ج متساویین الی المحیط. و ننزل أن ا ب وتر سبع الدور فتکون زاویة ا ج ب سبع زاویتین قائمتین و کل من زاویتی ا ب ج ب ا ج ثلثة أسباع زاویتین قائمتین. و نخرج الی ب ج مساویاً ا ب فتکون زاویة ا ه د ایضاً سبعی زاویتین قائمتین. و کنا أنزلنا زاویة ا ج ب سبع زاویتین قائمتین فزاویة ه د ایضاً سبع زاویتن قائمتین ف ج ه مثل ه د و خطوط ج ه ه د ا د ا ب الاربعة متساویة.
فترسل من نقطتی ا ه عمودی از ه ط علی ب ج فتکون نسبة ه ج الی ج ط کنسبة ا ج الی ج ز و ضرب ه ج فی ج ز مثل ضرب ا ج فی ج ط.
و أیضا لیکن ا ب واحداً فیکون وتر ثلث الدائرة اثنین و عمود المثلث الواقع فیها ثلثة و قطر الدائرة جذر خمسة اجزاء و ثلث >جذر<.
فتبین أن مربع ا ج اثنین و ثلثین و جذر خمسة اجزاء< وسبعة أتساع و هو ذو الاسمین الرابع و جذره و هو ا ج الاصم المسمی الاعظم و أن خط ج ز جذر اثنین و ثلثین و جذر خمسة و سبعة أتساع الا جذر نصف واحد إلا جذر ثلثة عشر ثمن ثمن و أن خط ج ط جذر ثلثی واحد و جذر ثلثة أتساع و ربع تسع إلا جذر نصف واحد إلا جذر ثلثة عشر ثمن ثمن فلیست نسبة ج ه الواحد الی ج ط کما تبین مقداره کنسبة ا ج الی ج ز ولا >ضرب< ج ه الواحد فی ج ز المذکور مقداره مثل ضرب ا ج فی ج ط المذکور مقدار هما.
و قد کان فی الحکم الاول ضرب ج ه فی ج ز مثل ضرب ا ج فی ج ط و هذا خلف. فلیس وتر سبع الدائرة بمساو لنصف وتر ثلثها و ذلک ما أردنا بیانه.
پینوشتها:
1- پژوهشگر تاریخ و فلسفه ریاضیات و عضو هیئت علمی دانشگاه صنعتی شریف.
2- از آقای اکبر زمانی، مدرس خانهی ریاضیات اصفهان که این عکسها را برای اینجانب فرستادهاند سپاسگزاری میکنم.
3- مرتضی فرشته نژاد، گره سازی و گره چینی در هنر معماری ایران، تهران، انتشارات انجمن آثار ملی، 1356، صص148-147.
4- J. P. Hogendijk Greek and Arabic Constroctions of the regular heptagon Arch: HIst. Exact Sci. 30: 197-330.
5- حسینی زمرشیدی، گره چینی در معماری اسلامی، و هنرهای دستی. تهران، 1365، ص 56.
6- جعفر آقایانی چاوشی، «نه ضعلی منتظم در ریاضیات و نقوش تزئینی اسلامی»، نامه علم و دین، سال 10 و 11 شمارههای 33-36 ص 16-17.
7- این اثبات را از مقاله زیر اقتباس کردهایم:
M. Vele "Construction approchée du n-gone" Mathéematique et péedagogie n 142 (2003) pp. 99-103.
8- J. Tropfke, Geschichte der Etementarmathematik, Band 4 Berlim 1940 pp. 254.
9- ابوالوفای بوزجانی. ترجمه کتاب تجارت التجارة ، به اهتمام جعفر آقایانی چاوشی چاپ تهران، 1389، انتشارات میراث مکتوب با همکاری انجمن فرهنگی ایران و فرانسه، صص38-37.
10- A. Düer, Underweysung der Messing mit dem Zirckel und Richtscheyt (Treatise on Mensuration with Compass and Ruler), 1525.
11- این برهان را از مقابله زیر اقتباس کردهایم:
S. A Josse "Concerming The Regular inscribed Heptagone" American Mathematical Monthly Vo 1.21. (1914) pp. 13-14.
12-F.Woepcke, L"Algebre d" Omar Alkhayyami, Paris 1851 pp.114-115 et. 125-126.
13- J.P.Hogendijk,"Abul-Jud"s Answer to a Question of al-Birumi Concernig the Regular Heptagone" Annals New fork Academy of Sciences vol. 500 (1987).pp. 175-184.
14. R.Rashed," Les Comstruction géométriques entre Géomérie et algebra: L"Epitre d"Abu al –Jud à al-Biruni" Arabic Sciences and Philosophy, vol. 20 (2010)pp.1-50.
آقایانی چاوشی، جعفر؛ (1390)، پژوهشهایی در تاریخ علم، تهران: مرکز پژوهشی میراث مکتوب، چاپ اول


























