نویسنده: گراهام پریست
مترجم: بهرام اسدیان

قواعد اعتبار چه در ما جابگیر شده باشند چه نشده باشند. ما نسبت به اعتبار یا عدم اعتبارشکل های گوناگون استنتاج ها مجهز به شهودهای قوی ای هستیم. به این استنتاج توجه کنید: «او زن است و بانکدار است؛ پس او بانکدار است.» واقعاً در مورد اعتباراین استنتاج دعوای زیادی نیست. همین طور در مورد عدم اعتبار این یکی: «او نجار است؛ پس هم نجار است هم بیسبال بازی می کند.»
ولی خیلی وقت ها شهود کاردستمان می دهد. نظرتان در مورد استنتاج زیر چیست؟
(مقدمه ها را بالای خط افقی نوشته ایم ونتیجه را زیر آن)
ملکه ثروتمند است. ملکه ثروتمند نیست.
خوک ها می توانند پرواز کنند.
مسلماً معتبر به نظر نمی رسد. ثروت ملکه، چه کم چه زیاد، ظاهراًهیچ ربطی به پرواز خوک ها ندارد.
نظرتان درباره ی این دوتا چیست؟
ملکه ثروتمند است.
ملکه ثروتمند است یا خوک ها می توانند پرواز کنند.
ملکه ثروتمند است یا خوک ها می توانند پرواز کنند. ملکه ثروتمند نیست.
خوک ها می توانند پرواز کنند.
اولی به نظر معتبر می آید. به نتیجه اش دقت کنید. منطقدان ها به جمله هایی مثل این جمله ترکیب فصلی (1)، و به هر یک ازعبارت های پیش و پس از«یا» فاصل (2) می گویند. چه وقت یک ترکیب فصلی صادق است؟ وقتی که یکی ازدو فاصل صادق باشد. پس، چون مقدمه صادق است نتیجه هم صادق است: دومی هم متعبر به نظر می رسد. در مقدمه ی اولش می دانیم دست کم یکی ازفاضل ها درست است، مقدمه ی دوم می گوید که کدام یک از آن ها نادرست است، پس آن دیگری باید درست باشد.
ولی مشکل این جاست که اگر این دواستنتاجِ آشکارا معتبر را یک جا جمع کنیم، به استنتاجی می رسیم که آشکارا نامعتبر است، مثلِ این:
ملکه ثروتمند است.
ملکه ثروتمند است یا خوک ها می توانند پرواز کنند. ملکه ثروتمند نیست.
خوک ها می توانند پرواز کنند.
ولی آخر چه طور می شود چنین چیزی غلط از آب در آید؟ مگر می شود استنتاج هایی معتبررا به هم بچسبانیم و دست آخراستنتاجی نامعتبرنصیبمان شود؟ اگردرهمه موقعیت ها همه ی مقدمات صادق باشند، نتایج نیز باید صادق باشند. وهمین طورنتایجی که از این نتایج به دست آمده اند؛
و همین طورتا وقتی به آخرین نتیجه برسیم. کجای کار خراب است؟
برای آن که جوابمان درست وقانع کننده باشد، اجازه دهید بر جزئیات داستان کمی بیش تر تمرکز کنیم. اول بهتراست جمله هایمان را با نماد نشان دهیم:
«خوک ها می تواند پرواز کنند» را با p و «ملکه ثروتمند است» را با q نشان می دهیم. با این کار، در واقع، استنتاجمان را فشرده ترو جمع و جورتر می کنیم. ولی فایده اش فقط این نیست. اگرلحظه ای بر این کار درنگ کنید، متوجه می شوید که این دو جمله ای که با حروف p و q نشانشان دادیم عملاً هیچ ارتباطی به ملکه وخوک و پرواز و این جورچیزها ندارند. این دوجمله می توانند به جای هرچیز دیگری هم بنشینند؛ بنابراین، می توانیم به مضمون و محتوایشان هیچ توجهی نکنیم. و این دقیقاً همان چیزی است که ازنمایش جملات با نماد انتظار داریم.
حالا می توانیم جمله ی «ملکه ی ثروتمند است یا خوک ها می توانند پرواز کنند» را به این شکل بنویسیم: «p یا q». منطقدان ها اغلب این جمله را این طور می نویسند: pvq. با «ملکه ثروتمند نیست» چه کنیم؟ بهتر است این جمله را اول چنین بازنویسی کنیم: «چنین نیست که ملکه ثروتمند است» (علامت نقیض را به اول جمله آوردیم) خب، از این به بعد با این جمله سر وکارداریم: «چنین نیست که q». منطقدان ها اغلب این جمله را این طور می نویسند:

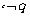و این طور می خوانندش: نقیض q. جمله هایی هم داریم مثل «ملکه ثروتمند است وخوک ها می توانند پرواز کنند».
یعنی «p و q». منطقدان ها اغلب این جمله را این طور می نویسند: p & q.
و اسم آن را ترکیب عطفیِ (3) p و q می گذارند، وخود p و q را هم عاطف (4) می نامند. با مجهز شدن به این تشکیلات، می توانیم آن استنتاج زنجیره ای کذا را این طور نمایش دهیم:

با این استنتاج چه باید کرد؟
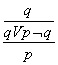
جمله های یا صادق اند یا کاذب. اجازه دهید T را نماد صدق و F را نماد کذب بگیریم. به پیروی از یکی از پایه گذاران منطق جدید، فیلسوف و ریاضیدان آلمانی، گوتلوب فرگه، به این T و F ارزش های صدق (5) می گویند. چه رابطه ای بین ارزش صدق جمله ی a و نقیض آن
(a

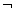
) وجود دارد؟ معمولاً پاسخ این است که اگریکی صادق باشد، دیگری کاذب است، و بالعکس. بنابراین، اگر«ملکه ثروتمند است» صادق باشد، «ملکه ثروتمند نیست» کاذب است، و بالعکس. این را می توان به شکل زیر نوشت: a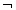 . ارزش T دارد اگر وتنها اگر a ارزش F داشته باشد.a 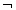. ارزش F دارد اگرو تنها اگر a ارزش T داشته باشد.
منطقدان ها به این دوقاعده شرط های صدقِ (6) نقیض می گویند. اگرفرض کنیم که هر جمله یا صادق است یا کاذب، و نه این که درآنِ واحد هم صادق باشد هم کاذب، می توانیم شرط های صدق نقیض را درجدول زیر نشان دهیم. منطقدان ها به این جدول ها صدق (7) می گویند:

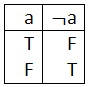
ارزش صدق a را درستون زیر آن نشان داده ایم. می بینیم که هر ارزشی a داشته باشد، ارزش
a 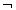عکس آن است، که آن را در ستون سمت راست نشان داده ایم.
جدول صدق ترکیب فصلی چگونه است؟ همان طور که قبلاً گفتم، شهود ما اکثراً بر آن است که ترکیب فصلیِ avb صادق است اگر یا a صادق باشد یا b (یا هردو). به عبارت دیگر، کل ترکیب فقط زمانی کاذب است که هر دو مؤلفه کاذب باشند:
avb ارزش T دارد اگر وتنها اگر دست کم یکی از دو مؤلفه ارزش T داشته باشد.
avb ارزش F دارد اگر وتنها اگرهردو مؤلفه ارزش F داشته باشد.
این شرط را می توانیم درجدول صدق زیرنشان دهیم:

avb	b a
F T T	T T F T T F F F

هر ردیف- به جز ردیف اول- نشانگر یک ترکیب احتمالی برای ارزش های a (ستون اول) و ارزش های b (ستون دوم) است. چهارترکیب احتمالی وجود دارد. و به همین دلیل به بیش ازچهار ردیف نیازی نداریم.
به ازای هرترکیب،ارزش متناظر avb در ستون راست داده شده.
و اما رابطه ی میان ارزش های صدق a و b و ارزش صدق a&b چیست؟
شهودمان می گوید a&b صادق است اگرهم a و هم b صادق باشند؛ درغیراین صورت کاذب است. به این ترتیب، مثلاً جمله ی «جان 35 سال دارد وموهایش قهوه ای است» صادق است اگرهم جمله ی «جان 35 سال دارد» و هم جمله ی «موهای جان قهوه ای است» صادق باشند. خلاصه کنیم:
a&b ارزش T دارد و تنها اگرهم a و هم b ارزش T داشته باشند.
a&b ارزش F دارد اگر وتنها اگر دست کم یکی از دو مؤلفه ارزش F داشته باشد.
شرط های صدق a&b را در جدول زیر نشان می دهیم:

a&b	b a
T F F F	T T F T T F F F

ولی این حرف ها اصلاً چه ربطی به مسئله ی اول این فصل دارد؟ اجازه دهید به سؤالی که آخر فصل قبل مطرح کردم بازگردم: موقعیت چیست؟
چیستیِ موقعیت به کنار؛ کار آن تعیین ارزش صدق جملات است.
بنابراین، مثلا، در یک موقعیت خاص، ممکن است صادق باشد که ملکه ثروتمند است و کاذب باشد که خوک ها می توانند پرواز کنند. درموقعیتی دیگر، ممکن است وضع کاملاً برعکس باشد (توجه کنید که این موقعیت ها مطلقاً فرضی اند!)
به عبارت دیگر، موقعیت مشخص می کند که هر جمله صادق است یا کاذب.
جمله های ما دراین مثال آخرهیچ موردی از «و»، «یا»، یا «چنین نیست که» ندارند. با اطلاعاتی که موقعیت دراختیار ما می گذارد، می توانیم ارزش صدق جمله هایی را که شامل چنین کلماتی هستند تعیین کنیم.

موقعیت زیر را در نظر بگیرید:

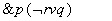
T : P
F : q
T : r

(r نماینده ی یک جمله است مثل «ریواس مغذی است» و ضمنا «P:T» یعنی به جمله ی p ارزش صدق T داده ایم). حالا بگویید ارزش صدق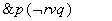 چیست؟ ارزش صدق این جمله را دقیقاً همان طور حساب می کنیم که می خواهیم مقدارعددی (2+6-)×3 را به دست آوریم. درمورد (2+6-)×3 چه کار می کنیم؟ ازجدول هایی استفاده می کنیم که حاصل ضرب ها وحاصل جمع ها را دراختیارمان می گذارد. r صادق است (ارزش صدقش T است). جدول صدق 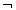می گوید که ارزش صدق 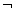r، F است. ولی چون ارزش q،F است، جدول صدق v می گوید که ارزش 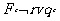است و نیز چون p ، T است، جدول صدق & می گوید که ارزش صدق 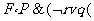است. با این روشِ گام به گام، می توانیم ارزش صدق هر زنجیره از جملات را که شامل&، V و 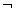باشد محاسبه کنیم.
در ضمن، ازفصل قبل به یاد دارید که گفتیم استنتاج به شرطی معتبراست که هیچ موقعیتی نباشد که درآن همه مقدمه ها صادق و نتیجه ناصادق (کاذب باشد. مثلاً به استنتاج q/ qvp توجه کنید، که قبلاً هم با آن روبه رو شدیم (از این به بعد، استنتاج را در یک خط می نویسم تا بودجه ی انتشارات دانشگاه آکسفورد را برباد ندهم!). جملات موجود فقط p و q هستند. بنابراین، فقط چهار ترکیب احتمالی برای ارزش های صدق وجود دارد. به ازای هریک از این چهار تا می توانیم ارزش صدق مقدمه و نتیجه را به دست آوریم. حاصل را به شکل زیر نمایش می دهیم:

qvp

P q

T
T
T
F

T
T
F
F

T      T
F       T
T       F
F       F

دو ستون اول، همه ی ترکیب های ممکن برای ارزش های صدق q و p را نشان می دهند، وستون آخرارزش های صدق متناظر با مقدمه و نتیجه را.
ستون سوم عین ستون اول است. این وضع در مورداستنتاج های خاصی پیش می آید که مقدمه تصادفاً خودش یکی ازجملات اصلی است. ستون چهارم را از روی جدول صدق 7 می نویسیم. با این اطلاعات، می توانیم به راحتی بفهمیم که چرا استنتاج مذکور معتبر است؛ چون هیچ ردیفی نیست که در آن مقدمه (q) صادق و نتیجه (qvp) کاذب باشد.
و اما استنتاج
qvp ,
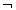q/p. به همان شیوه ی قبلی عمل می کنیم:

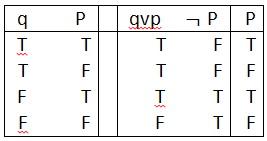
این بار ستون پنجمی هم در کار است، چون دو مقدمه داریم. ارزش های صدق مقدمه ها و نتیجه را، به ترتیب، بنابر جدول صدق ترکیب فصلی و نقیض به دست می آوریم. در این مثال نیزهیچ ستونی نیست که در آن، همه مقدمه ها صادق و نتیجه کاذب باشد. پس استنتاج معتبر است.
اولین استنتاج این فصل چه طور؟ معتبراست یا نه؟ این استنتاج به زبان منطق این طور ترجمه می شود: q, -q/p. باز هم به روش قبل:

باز هم استنتاج معتبر است. ولی این بار دیگر چرا؟ چون هیچ ردیفی نیست که در آن هر دو مقدمه صادق و نتیجه کاذب باشد. در واقع، اصلاً هیچ ردیفی نیست که درآن هر دو مقدمه صادق باشند. نتیجه هم که اصلاً اهمیتی ندارد! گاهی منطقدان ها به اعتبار این استنتاج ها اعتبارهای پوچ (8) می گویند، چون هرگز ممکن نیست که دراین استنتاج ها هر دو مقدمه در آنِ واحد صادق باشند.
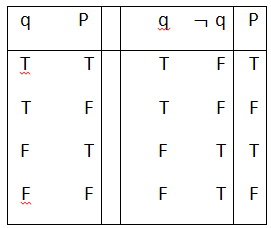
شاید مشکلی که در ابتدای مقاله با آن مواجه شدیم همین جا حل شده باشد. این جاست که می فهمیم شهود ابتدایی و خام ما درمورد این استنتاج غلط بوده است. به هرحال، شهود اغلب گمراهمان می کند. تقریباً به نظرهمه ی ما بدیهی است که زمین ساکن است، اما اگر یک دوره ی ابتدایی فیزیک بگذرانیم، می فهمیم که این طور نیست؛ چون زمین با سرعت درفضا حرکت می کند. علاوه بر این، می توان توضیح داد که چرا شهودهای منطقی هم گاهی به راه خطا می رود. اکثر استنتاج هایی که در زندگی روزمره با آن ها سروکارداریم ازجنس استنتاج هایی نیستند که اعتبارشان پوچ باشد. شهودهای ما مقید به بسیاری چیزها هستند وصدق کلی ندارند- درست مثل آموخته هایمان موقع یادگیری راه رفتن (مثلا، بدنمان را خم نکنیم،) که درموارد دیگری لزوماً درست نیست (مثلاً، موقع یادگیری دوچرخه سواری).
مشکل این جاست که مسائل همیشه آن قدرها هم که انتظار داریم ساده و سرراست نیستند. بنابراصول سیستم ما، ارزش صدق جمله ی a ¬ را کاملاً می توانیم از روی ارزش صدق جمله ی a تعیین کنیم. به همین شکل، ارزش های صدق جملات avb و a&b کاملاً از روی ارزش صدق جمله ی a تعیین می شوند. منطقدان ها به عملگردهایی مانندv، & و

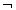
تابع ارزش (9) می گویند. ولی دلایل محکم و خوبی داریم که نشان می دهند کلماتی مثل «یا» و «و» تابع ارزش نیستند- یا دست کم گاهی هستند، گاهی نیستند.
مثلا، مطابق جدول صدق &، ارزش جمله ی «a وb» همیشه با ارزش صدق جمله ی «b و a» یکی ست. یعنی، هر دوجمله زمانی صادق اند که a و b، هر دو، صادق باشند. درغیر این صورت، هر دو جمله کاذب می شوند.
حالا به جمله های زیر دقت کنید:
1. جان سرش به جایی خورد و زمین خورد.
2. جان زمین خورد و سرش به جایی خورد.
جمله ی اول می گوید جان سرش به جایی خورد و بعد زمین خورد.
جمله ی دوم می گوید جان زمین خورد و بعد سرش به جایی خورد. مسلماً ممکن است در شرایطی جمله ی اول صادق و جمله ی دوم کاذب باشد، و بالعکس. پس فقط ارزش صدق عاطف ها نیست که مهم است؛ این هم مهم است که کدام عاطف علت آن دیگری بوده است.
این وضع گریبان «یا» را هم می گیرد. مطابق قوانین جدول های صدق، «a یا b» صادق است اگر یا a صادق باشد یا b (یا هر دو). ولی فرض کنید دوستی بگوید:
یا الان می آیی یا دیرمان می شود.
و شما هم می آیید. مطابق جدول های صدق v، این ترکیب فصلی صادق است، ولی فرض کنید شما بعداً می فهمید که دوستتان به شما کلک زده؛ یعنی می فهمید که می توانستید ازخانه نیم ساعت بعد خارج شوید وهمچنان سروقت به قرارتان برسید. دراین شرایط، حتماً با خود می گویید دوستتان دروغ گفته؛ آنچه گفته کاذب بوده. بازهم می فهمیم که صرفاً ارزش صدق فاصل ها نیست که مهم است؛ وجود نوعی اتصال میان آن ها نیز مهم است.
خب، دیگر بهتر است پرحرفی نکنم، و بگذارم خودتان به این مسئله فکر کنید. جدول های صدق روش کار آمدی دراختیار ما می گذارند که رفتار بعضی از استنتاج های منطقی را نشان می دهد.
روش مکانیکی مورد بحث فقط از پس تبیین رفتار بعضی از انواع استنتاج بر می آید. چه بسیار استنتاج های دیگری هم هستند که تن به این روش نمی دهند. یادمان نرود که ما تازه اول راهیم.

پی نوشت ها :

1-disjunction
2- disjunct
3- conjunction
4- conjunct
5- truth values
6- truth conditions
7- truth table
8- vacuously valid
9- truth function

منبع مقاله :
پریست، گراهام،(1386)، منطق، مترجم: بهرام اسدیان، تهران: نشر ماهی، چاپ سوم