
نویسنده: گراهام پریست
مترجم: بهرام اسدیان
مترجم: بهرام اسدیان
امکان ندارد کیهان توده ای باشد محصول تصادفی محض. کیهان نظم و نظام های بسیار خاص و شاخصی از خود نشان می دهد: ماده شکل کهکشان ها را به خود می گیرد، که این ها نیز به نوبه ی خود شکل ستارگان ونظام های سیاره ای را به خود می گیرند. و در بعضی از این نظام ها ماده به شکلی در می آید که می توان موجودات زنده ای مثل من و شما را ایجاد کند. چه توضیحی برای این نظام و نظام دارید؟ شاید بگویید که قوانین فیزیک و زیست شناسی این توضیح را دراختیار می گذارند. بله، شاید هم بگذارند. ولی چرا قوانین فیزیک و زیست شناسی به همین گونه ای که هستند هستند؟ به هر حال، کاملاً می شد این قوانین غیر از آن چیزی که هستند باشند. مثلاً ممکن بود گرانش نیروی دافعه می شد نه جاذبه، که در این صورت، هرگز تکه های بزرگ و استوار ماده در کار نمی بود، و حیات، آن گونه که ما می شناسیم، در هیچ جای این کیهان به هیچ صورتی شکل نمی گرفت. آیا همه ی این حرف ها دلیل قاطع و فوق العاده ای برای باور به وجود خالقی برای کیهان به دست نمی دهند؟ دلیلی برای باور به موجودی فهیم و آگاه که این کیهان را به همراه قوانین فیزیکی و زیست شناختی اش به هدفی به وجود آورده است؟ یک کلام، آیا این واقعیت که نظم و نظام کیهان این قدر دقیق است باعث نمی شود به وجود خدا باور بیاوریم؟
غالباً این برهان را «برهان اثبات وجود خدا از نظم عالم» می خوانند، که البته بهتر بود آن را«برهان اثباتِ نظم عالم» می خواندند. ولی بهتر است فعلاً خودمان را معطل این مسئله نکنیم و حواسمان را جای دیگر متمرکز کنیم. مقدمه ی برهان، o، بر این اساس طراحی شده که کیهان نظمی خاص دارد. نتیجه،g به وجود خدایی خالق صحه می گذارد. احتمالo بسیار پایین است؛ زمانی بالا می رود که gصادق باشد. پس g محتمل است ولی به فرض o.
شکی نیست که احتمال شرطی o به فرض صدق g بسیار بیش تر از احتمال o به فرض صدقg است. یعنی:
است. یعنی:
 ولی این چیزی نیست که دنبالش بودیم. برای آن که o دلیل استقراییِ خوبی g برای باشد، باید احتمال g به فرض o بیش تر از احتمال نقیض به g به فرض o باشد. یعنی:
ولی این چیزی نیست که دنبالش بودیم. برای آن که o دلیل استقراییِ خوبی g برای باشد، باید احتمال g به فرض o بیش تر از احتمال نقیض به g به فرض o باشد. یعنی:
 در ضمن باید بدانیم که اگر(pr( o |g زیاد باشد، لزوماً به این معنا نیست که pr( g |o) نیز زیاد است. مثلاً اگر کانگورویی آزاد در طبیعت اطرافتان ببینید، احتمال این که در استرالیا باشید بسیار زیاد است (اگر چنین موجودی را هر جایی از دنیا به جز استرالیا دیدید، بدانید که به احتمال زیاد از باغ وحش فرار کرده است). ولی احتمال این که کانگورویی آزاد در طبیعت اطرافتان ببینید بسیار کم است (خود من بعد از ده سال زندگی در استرالیا، فقط یک کانگوروی وحشی دیدم).
در ضمن باید بدانیم که اگر(pr( o |g زیاد باشد، لزوماً به این معنا نیست که pr( g |o) نیز زیاد است. مثلاً اگر کانگورویی آزاد در طبیعت اطرافتان ببینید، احتمال این که در استرالیا باشید بسیار زیاد است (اگر چنین موجودی را هر جایی از دنیا به جز استرالیا دیدید، بدانید که به احتمال زیاد از باغ وحش فرار کرده است). ولی احتمال این که کانگورویی آزاد در طبیعت اطرافتان ببینید بسیار کم است (خود من بعد از ده سال زندگی در استرالیا، فقط یک کانگوروی وحشی دیدم).
بهpr( g |o) وpr( o |g) احتمالات معکوس(1) می گویند. در مورد برهان نظم، دیدیم که برای موفق از آب درآمدن آن، ارتباط میان احتمالات معکوس باید چنان باشد که از جمله ی 1 به جمله ی 2 برسیم. رابطه ی میان احتمالات معکوس بسیار ساده است. معادله ی cpرا به یاد دارید؟
pr( a |b)=pr(a&b)/pr(b)
در نتیجه:
3. pr( a |b)×pr(b)=pr(a&b)
مشابهاً:
pr( b |a)=pr(b&a)/pr(a)
در نتیجه:
4. pr( b |a)×pr(a)=pr(b & a)
ولی pr(b & a) = pr(a & b) ( چون a&bو b&a در موقعیت های کاملاً عین هم صادق هستند.) پس بنابر 3 و 4:
pr( a |b)×pr(b)=pr( b |a)×pr(a)
فرض کنید (pr(b صفر نباشد- من از این جور فرض ها خواهم کرد و توضیح بیش تری هم نخواهم داد- در این صورت، می توانیم همین معادله ی بالا را به این شکل بازنویسی می کنیم:
pr( a |b)=pr( b |a)×pr(a)/pr(b):Inv
رابطه ای میان احتمالات معکوس همین است ( برای از بر کردنِ این رابطه، بد نیست به یاد داشته باشید که در طرف راست معادله، اول b ی داریم که بعدش a می آید، و بعد a ی داریم که به دنبالش b می آید).
اگر Inv را در احتمالات معکوس جمله ی شماره ی 1 به کار ببریم، خواهیم داشت:
 pr(o) را از دو طرف معادله خط می زنیم:
pr(o) را از دو طرف معادله خط می زنیم:
 حالا می توانیم معادله را به این شکل بنویسیم:
حالا می توانیم معادله را به این شکل بنویسیم:
 می دانید که شرط توفیق برهان نظم رسیدن به 2 است، یعنی باید:
می دانید که شرط توفیق برهان نظم رسیدن به 2 است، یعنی باید:
 ظاهراً تنها چیزی که می تواند ما را از 5 به 2 برساند این است که
ظاهراً تنها چیزی که می تواند ما را از 5 به 2 برساند این است که که یعنی:
که یعنی:

به ارزش های pr(g) و ( احتمالات پیشین(2) می گویند؛ یعنی این که احتمالاتg و
( احتمالات پیشین(2) می گویند؛ یعنی این که احتمالاتg و
 پیش از بررسی و ملاحظه ی هر گونه شاهد و گواهی (مثل o) مطرح می شوند. پس، آنچه بدان نیاز داریم تا بتوانیم به کمک آن اعتبار برهان را به تصویب برسانیم این است که نشان دهیم احتمال پیشینِ وجود خدایی خالق بیش تر از (یا مساوی با) احتمال پیشینِ نبودِ آن است.
پیش از بررسی و ملاحظه ی هر گونه شاهد و گواهی (مثل o) مطرح می شوند. پس، آنچه بدان نیاز داریم تا بتوانیم به کمک آن اعتبار برهان را به تصویب برسانیم این است که نشان دهیم احتمال پیشینِ وجود خدایی خالق بیش تر از (یا مساوی با) احتمال پیشینِ نبودِ آن است.
ولی آیا واقعاً این طور است؟ متأسفانه هیچ دلیلی برای باور به این حرف نداریم. انگار که اصلاً ماجرا چیز دیگری است. فرض کنید شما نمی دانید امروز کدام روز هفته است. ضمناً فرض کنید که m یعنی امروز دوشنبه است. پس
 یعنی امروز دوشنبه نیست. کدام یک محتمل تر است؟ mیا
یعنی امروز دوشنبه نیست. کدام یک محتمل تر است؟ mیا  ؟ قطعاً
؟ قطعاً  ، چون تعداد روزهایی که ممکن است دوشنبه نباشد شش روز است ولی فقط یک روز می تواند دوشنبه باشد(
، چون تعداد روزهایی که ممکن است دوشنبه نباشد شش روز است ولی فقط یک روز می تواند دوشنبه باشد( پنج شنبه، چهارشنبه، سه شنبه و.. را در بر می گیرد). وضع خدا هم همین طور است. مسلماً می شد کیهان به هزار شکل مختلف به وجود بیاید. و در ضمن، شهود ما هم این را می گوید که فقط چند طریقِ ایجاد جهان، نظم خاص و چشمگیری می تواند داشته باشد: نظم چیز بسیار خاصی است. و در واقع اساس برهان نظم بر همین استوار است. اما در این حالت، کیهان های ممکنی که در آن ها ناظمی وجود داشته باشد، نسبتاً اندک خواهند بود. پس به نحو پیشینی(3) احتمال عدم وجود خالق بسیار بیش تر از احتمال وجود آن است.
پنج شنبه، چهارشنبه، سه شنبه و.. را در بر می گیرد). وضع خدا هم همین طور است. مسلماً می شد کیهان به هزار شکل مختلف به وجود بیاید. و در ضمن، شهود ما هم این را می گوید که فقط چند طریقِ ایجاد جهان، نظم خاص و چشمگیری می تواند داشته باشد: نظم چیز بسیار خاصی است. و در واقع اساس برهان نظم بر همین استوار است. اما در این حالت، کیهان های ممکنی که در آن ها ناظمی وجود داشته باشد، نسبتاً اندک خواهند بود. پس به نحو پیشینی(3) احتمال عدم وجود خالق بسیار بیش تر از احتمال وجود آن است.
انگار برهان نظم منتفی شد. برهان نظم فریبنده است چون مردم اغلب احتمالات را با معکوسشان عوضی می گیرند، و به همین دلیل، از کنار بخش بسیار حیاتی برهان سرسری می گذرند.
بسیاری از برهان های استقرایی ما را مجبور می کنند تا درباره ی احتمالاتِ معکوس فکر کنیم و موضع مان را شفاف کنیم؛ که البته برهان نظم از این حیث برهان خاص و عجیبی نیست. اجازه دهید توضیح دهم چرا. فرض کنید به یکی از کازینوهای محلی رفته اید. در آن جا دو دستگاه رولت می بینید
(اسمشان را A و B می گذاریم). دوستی به شما گفته که یکی از آن ها دستکاری شده، ولی نگفته کدام یک. یعنی دستگاه طوری تنظیم شده که به جای آن که نیمی ازدفعات چرخش قرمز را برنده اعلام کند و نیمی دیگر سیاه را (کما این که دستگاهی که درآن تقلب نکرده اند همین طور عمل می کند)، دفعات حتماً قرمز را برنده اعلام می کند و
دفعات حتماً قرمز را برنده اعلام می کند و  سیاه را (البته ناگفته نماند که دستگاه های رولت واقعی واصیل، هر از گاهی سبز را هم برنده اعلام می کنند؛ ولی برای ساده کردن مسئله، این نکته را در نظر نمی گیریم). حالا فرض کنید که مشغول تماشای یکی از این دو دستگاه هستید، مثلاً دستگاه A، بعد از پنج چرخش متوالی، این نتایج به دست می آید:
سیاه را (البته ناگفته نماند که دستگاه های رولت واقعی واصیل، هر از گاهی سبز را هم برنده اعلام می کنند؛ ولی برای ساده کردن مسئله، این نکته را در نظر نمی گیریم). حالا فرض کنید که مشغول تماشای یکی از این دو دستگاه هستید، مثلاً دستگاه A، بعد از پنج چرخش متوالی، این نتایج به دست می آید:
R, R, R, R, B
(که R یعنی قرمز، و Bیعنی سیاه). آیا حق دارید نتیجه بگیرید که این همان چرخشی است که دستکاری شده؟ فرض کنید c نماینده ی جمله ای با این مضمون باشد که دنباله ی خاص بالا برنده می شود و f نماینده ی این جمله است که چرخ A دستکاری شده. حالا سؤالمان را این طور مطرح می کنیم: آیا استنتاج f از c استنتاج استقرایی خوبی است؟
یعنی باید بفهمیم که آیا () یا نه. از معادله ی Inv کمک می گیریم تا نامساوی بالا را به رابطه ای میان احتمالات معکوس تبدیل کنیم؛ خواهیم داشت:
() یا نه. از معادله ی Inv کمک می گیریم تا نامساوی بالا را به رابطه ای میان احتمالات معکوس تبدیل کنیم؛ خواهیم داشت:
 هر دو طرف را درpr(c) ضرب می کنیم:
هر دو طرف را درpr(c) ضرب می کنیم:
 آیا این ادعا صادق است؟ پیش از هر چیز ببینیم احتمال f و
آیا این ادعا صادق است؟ پیش از هر چیز ببینیم احتمال f و
 ( که احتمال های پیشین هستند) چه قدر است؟ می دانیم که یا A ستکاری شده یاB، ( ولی نه هر دو). برای این که بفهمیم چرخ دنباله ی بالا را تولید کرده یا ، هیچ دلیلی به نفع هیچ کدام نداریم. یعنی احتمال این که چرخ کذایی A باشد
( که احتمال های پیشین هستند) چه قدر است؟ می دانیم که یا A ستکاری شده یاB، ( ولی نه هر دو). برای این که بفهمیم چرخ دنباله ی بالا را تولید کرده یا ، هیچ دلیلی به نفع هیچ کدام نداریم. یعنی احتمال این که چرخ کذایی A باشد  است و احتمال این که باشد هم
است و احتمال این که باشد هم است. به عبارت دیگر
است. به عبارت دیگر  pr(f)= و
pr(f)= و  . بنابراین، می توانیم این دو را از دو طرف نامعادله ای بالا حذف کنیم:
. بنابراین، می توانیم این دو را از دو طرف نامعادله ای بالا حذف کنیم:

احتمال مشاهده ی دنباله ای که با c نشانش دادیم، با این فرض که چرخ به همان نحوی که گفتیم دستکاری شده ( که خلاصه یعنی )،
)،  (است (اصلاً مهم نیست اگر نمی دانید چرا؛ می توانید به حرف های من اعتماد کنید)، که حاصلش می شود،
(است (اصلاً مهم نیست اگر نمی دانید چرا؛ می توانید به حرف های من اعتماد کنید)، که حاصلش می شود،  ، یعنی تا 0/079 کار می کند. اما احتمال این که دنباله برنده شود، با فرض این که چرخ دستکاری نشده و بنابراین همه چیز منصفانه و عادلانه است (که خلاصه یعنی )،
، یعنی تا 0/079 کار می کند. اما احتمال این که دنباله برنده شود، با فرض این که چرخ دستکاری نشده و بنابراین همه چیز منصفانه و عادلانه است (که خلاصه یعنی )،  p است (این بار هم می توانید به حرف های من اعتماد کنید، البته اگر می خواهید)، یعنی تا 0/031 کار می کند. کم تر از 0/079 است. پس استنتاج معتبر است.
p است (این بار هم می توانید به حرف های من اعتماد کنید، البته اگر می خواهید)، یعنی تا 0/031 کار می کند. کم تر از 0/079 است. پس استنتاج معتبر است.
فهمیدن روشی که بنابر آن احتمالات پیشین را به دست آوردیم مهم است. دو احتمال داشتیم: یا چرخ A دستکار شده یا چرخ B؛ هیچ اطلاعات دیگری هم نداشتیم تا بتوانیم میان دو احتمال فرق بگذاریم. پس یک احتمال را به آن ها نسبت دادیم. این نمونه ای است از کاربرد اصل عدم تفاوت(4)؛ بنابراین اصل، وقتی چند احتمال داریم که تفاوت خاصی میان آن ها نیست، همه ی آن ها به یک اندازه محتمل اند. پس اگرN احتمال داشته باشیم. احتمال هر یک است اصل عدم تفاوت به نوعی از جنس اصل تقارن(5) است.
است اصل عدم تفاوت به نوعی از جنس اصل تقارن(5) است.
توجه داشته باشید که این اصل را نمی توانستم دربرهان نظم به کار گیریم. در مورد دستگاه های رولت، دو موقعیتِ ممکن داشتیم که کاملاً متقارن بودند: چرخ A دستکاری شده، چرخ B دستکاری شده، در برهان نظم هم دو موقعیت در کار بود: خدای خالق وجود دارد، خدای خالق وجود ندارد. ولی تقارن این دوموقعیت فقط در این حد است که بگوییم: امروز دوشنبه است، امروز دوشنبه نیست. همان طور که دیدیم، موقعیت ها و جهان های ممکنی که در آن ها هیچ خالقی نیست بسیار بیش تر از آن موقعیت هایی است که خالق در آن ها وجود دارد.
اصل عدم تفاوت بخش مهمی از استدلال های شهودی ما در باب احتمالات است. اجازه دهید این مقاله را با ذکر این نکته تمام کنم که بگویم اصل عدم تفاوت هم خالی از ایراد نیست. حالا دیگر تقریباً همه می دانند که در بعضی از کاربردهای این اصل به تناقض دچار می شویم.
فرض کنید ماشینی بریزِبین را به مقصد شهری در فاصله ی 300 کیلومتری ترک می کند. متوسط سرعت ثابت ماشین بین km/h 50 و km/h 100 است. احتمال زمان رسیدن مسافر راچگونه توضیح دهیم؟ خب، اگر با km/h 100 برود، ساعت 3 بعداز ظهر می رسد؛ و اگر با سرعت km/h 50 برود، 6 بعداز ظهر می رسد. پس ساعتی بین این دو زمان می رسد. نقطه ی میانی این دو زمان 4:30 بعدازظهر است. بنابر اصل عدم تفاوت، همان قدر محتمل است که قبل از 4:30 برسد که بعد از آن. ولی سرعت میان km/h 50 و km/h 100، km/h 75 است. دوباره، بنابراین اصل، همان قدر محتمل است که ماشین ما بالای km/h 75 برود که زیر آن. اگر با سرعتkm/h 75 برود، 4 بعدازظهر می رسد. پس همان قدر محتمل است که قبل از 4 بعداز ظهر برسد که بعد از آن. پس احتمال این که قبل از 4:30 بعدازظهر برسد بیش تر از آن است که بعد از 4:30 برسد
خب، بس است! دنبالش را خودتان بگیرید. درباره ی احتمال در حد یک مقاله به قدر کافی پرچانگی کردم!
پریست، گراهام،(1386)، منطق، مترجم: بهرام اسدیان، تهران: نشر ماهی، چاپ سوم
غالباً این برهان را «برهان اثبات وجود خدا از نظم عالم» می خوانند، که البته بهتر بود آن را«برهان اثباتِ نظم عالم» می خواندند. ولی بهتر است فعلاً خودمان را معطل این مسئله نکنیم و حواسمان را جای دیگر متمرکز کنیم. مقدمه ی برهان، o، بر این اساس طراحی شده که کیهان نظمی خاص دارد. نتیجه،g به وجود خدایی خالق صحه می گذارد. احتمالo بسیار پایین است؛ زمانی بالا می رود که gصادق باشد. پس g محتمل است ولی به فرض o.
شکی نیست که احتمال شرطی o به فرض صدق g بسیار بیش تر از احتمال o به فرض صدقg
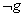 است. یعنی:
است. یعنی: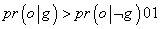
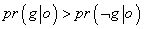
بهpr( g |o) وpr( o |g) احتمالات معکوس(1) می گویند. در مورد برهان نظم، دیدیم که برای موفق از آب درآمدن آن، ارتباط میان احتمالات معکوس باید چنان باشد که از جمله ی 1 به جمله ی 2 برسیم. رابطه ی میان احتمالات معکوس بسیار ساده است. معادله ی cpرا به یاد دارید؟
pr( a |b)=pr(a&b)/pr(b)
در نتیجه:
3. pr( a |b)×pr(b)=pr(a&b)
مشابهاً:
pr( b |a)=pr(b&a)/pr(a)
در نتیجه:
4. pr( b |a)×pr(a)=pr(b & a)
ولی pr(b & a) = pr(a & b) ( چون a&bو b&a در موقعیت های کاملاً عین هم صادق هستند.) پس بنابر 3 و 4:
pr( a |b)×pr(b)=pr( b |a)×pr(a)
فرض کنید (pr(b صفر نباشد- من از این جور فرض ها خواهم کرد و توضیح بیش تری هم نخواهم داد- در این صورت، می توانیم همین معادله ی بالا را به این شکل بازنویسی می کنیم:
pr( a |b)=pr( b |a)×pr(a)/pr(b):Inv
رابطه ای میان احتمالات معکوس همین است ( برای از بر کردنِ این رابطه، بد نیست به یاد داشته باشید که در طرف راست معادله، اول b ی داریم که بعدش a می آید، و بعد a ی داریم که به دنبالش b می آید).
اگر Inv را در احتمالات معکوس جمله ی شماره ی 1 به کار ببریم، خواهیم داشت:
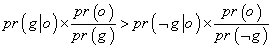
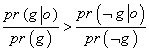
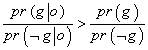
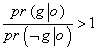
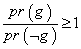 که یعنی:
که یعنی: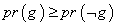
به ارزش های pr(g) و
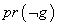 ( احتمالات پیشین(2) می گویند؛ یعنی این که احتمالاتg و
( احتمالات پیشین(2) می گویند؛ یعنی این که احتمالاتg و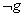 پیش از بررسی و ملاحظه ی هر گونه شاهد و گواهی (مثل o) مطرح می شوند. پس، آنچه بدان نیاز داریم تا بتوانیم به کمک آن اعتبار برهان را به تصویب برسانیم این است که نشان دهیم احتمال پیشینِ وجود خدایی خالق بیش تر از (یا مساوی با) احتمال پیشینِ نبودِ آن است.
پیش از بررسی و ملاحظه ی هر گونه شاهد و گواهی (مثل o) مطرح می شوند. پس، آنچه بدان نیاز داریم تا بتوانیم به کمک آن اعتبار برهان را به تصویب برسانیم این است که نشان دهیم احتمال پیشینِ وجود خدایی خالق بیش تر از (یا مساوی با) احتمال پیشینِ نبودِ آن است.ولی آیا واقعاً این طور است؟ متأسفانه هیچ دلیلی برای باور به این حرف نداریم. انگار که اصلاً ماجرا چیز دیگری است. فرض کنید شما نمی دانید امروز کدام روز هفته است. ضمناً فرض کنید که m یعنی امروز دوشنبه است. پس
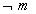 یعنی امروز دوشنبه نیست. کدام یک محتمل تر است؟ mیا
یعنی امروز دوشنبه نیست. کدام یک محتمل تر است؟ mیا 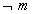 ؟ قطعاً
؟ قطعاً 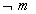 ، چون تعداد روزهایی که ممکن است دوشنبه نباشد شش روز است ولی فقط یک روز می تواند دوشنبه باشد(
، چون تعداد روزهایی که ممکن است دوشنبه نباشد شش روز است ولی فقط یک روز می تواند دوشنبه باشد(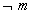 پنج شنبه، چهارشنبه، سه شنبه و.. را در بر می گیرد). وضع خدا هم همین طور است. مسلماً می شد کیهان به هزار شکل مختلف به وجود بیاید. و در ضمن، شهود ما هم این را می گوید که فقط چند طریقِ ایجاد جهان، نظم خاص و چشمگیری می تواند داشته باشد: نظم چیز بسیار خاصی است. و در واقع اساس برهان نظم بر همین استوار است. اما در این حالت، کیهان های ممکنی که در آن ها ناظمی وجود داشته باشد، نسبتاً اندک خواهند بود. پس به نحو پیشینی(3) احتمال عدم وجود خالق بسیار بیش تر از احتمال وجود آن است.
پنج شنبه، چهارشنبه، سه شنبه و.. را در بر می گیرد). وضع خدا هم همین طور است. مسلماً می شد کیهان به هزار شکل مختلف به وجود بیاید. و در ضمن، شهود ما هم این را می گوید که فقط چند طریقِ ایجاد جهان، نظم خاص و چشمگیری می تواند داشته باشد: نظم چیز بسیار خاصی است. و در واقع اساس برهان نظم بر همین استوار است. اما در این حالت، کیهان های ممکنی که در آن ها ناظمی وجود داشته باشد، نسبتاً اندک خواهند بود. پس به نحو پیشینی(3) احتمال عدم وجود خالق بسیار بیش تر از احتمال وجود آن است.انگار برهان نظم منتفی شد. برهان نظم فریبنده است چون مردم اغلب احتمالات را با معکوسشان عوضی می گیرند، و به همین دلیل، از کنار بخش بسیار حیاتی برهان سرسری می گذرند.
بسیاری از برهان های استقرایی ما را مجبور می کنند تا درباره ی احتمالاتِ معکوس فکر کنیم و موضع مان را شفاف کنیم؛ که البته برهان نظم از این حیث برهان خاص و عجیبی نیست. اجازه دهید توضیح دهم چرا. فرض کنید به یکی از کازینوهای محلی رفته اید. در آن جا دو دستگاه رولت می بینید
(اسمشان را A و B می گذاریم). دوستی به شما گفته که یکی از آن ها دستکاری شده، ولی نگفته کدام یک. یعنی دستگاه طوری تنظیم شده که به جای آن که نیمی ازدفعات چرخش قرمز را برنده اعلام کند و نیمی دیگر سیاه را (کما این که دستگاهی که درآن تقلب نکرده اند همین طور عمل می کند)،
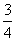 دفعات حتماً قرمز را برنده اعلام می کند و
دفعات حتماً قرمز را برنده اعلام می کند و 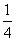 سیاه را (البته ناگفته نماند که دستگاه های رولت واقعی واصیل، هر از گاهی سبز را هم برنده اعلام می کنند؛ ولی برای ساده کردن مسئله، این نکته را در نظر نمی گیریم). حالا فرض کنید که مشغول تماشای یکی از این دو دستگاه هستید، مثلاً دستگاه A، بعد از پنج چرخش متوالی، این نتایج به دست می آید:
سیاه را (البته ناگفته نماند که دستگاه های رولت واقعی واصیل، هر از گاهی سبز را هم برنده اعلام می کنند؛ ولی برای ساده کردن مسئله، این نکته را در نظر نمی گیریم). حالا فرض کنید که مشغول تماشای یکی از این دو دستگاه هستید، مثلاً دستگاه A، بعد از پنج چرخش متوالی، این نتایج به دست می آید:R, R, R, R, B
(که R یعنی قرمز، و Bیعنی سیاه). آیا حق دارید نتیجه بگیرید که این همان چرخشی است که دستکاری شده؟ فرض کنید c نماینده ی جمله ای با این مضمون باشد که دنباله ی خاص بالا برنده می شود و f نماینده ی این جمله است که چرخ A دستکاری شده. حالا سؤالمان را این طور مطرح می کنیم: آیا استنتاج f از c استنتاج استقرایی خوبی است؟
یعنی باید بفهمیم که آیا
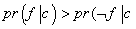 () یا نه. از معادله ی Inv کمک می گیریم تا نامساوی بالا را به رابطه ای میان احتمالات معکوس تبدیل کنیم؛ خواهیم داشت:
() یا نه. از معادله ی Inv کمک می گیریم تا نامساوی بالا را به رابطه ای میان احتمالات معکوس تبدیل کنیم؛ خواهیم داشت: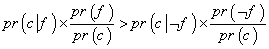
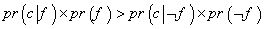
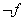 ( که احتمال های پیشین هستند) چه قدر است؟ می دانیم که یا A ستکاری شده یاB، ( ولی نه هر دو). برای این که بفهمیم چرخ دنباله ی بالا را تولید کرده یا ، هیچ دلیلی به نفع هیچ کدام نداریم. یعنی احتمال این که چرخ کذایی A باشد
( که احتمال های پیشین هستند) چه قدر است؟ می دانیم که یا A ستکاری شده یاB، ( ولی نه هر دو). برای این که بفهمیم چرخ دنباله ی بالا را تولید کرده یا ، هیچ دلیلی به نفع هیچ کدام نداریم. یعنی احتمال این که چرخ کذایی A باشد 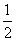 است و احتمال این که باشد هم
است و احتمال این که باشد هم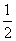 است. به عبارت دیگر
است. به عبارت دیگر 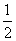 pr(f)= و
pr(f)= و 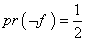 . بنابراین، می توانیم این دو را از دو طرف نامعادله ای بالا حذف کنیم:
. بنابراین، می توانیم این دو را از دو طرف نامعادله ای بالا حذف کنیم: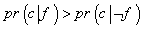
احتمال مشاهده ی دنباله ای که با c نشانش دادیم، با این فرض که چرخ به همان نحوی که گفتیم دستکاری شده ( که خلاصه یعنی
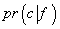 )،
)، 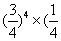 (است (اصلاً مهم نیست اگر نمی دانید چرا؛ می توانید به حرف های من اعتماد کنید)، که حاصلش می شود،
(است (اصلاً مهم نیست اگر نمی دانید چرا؛ می توانید به حرف های من اعتماد کنید)، که حاصلش می شود، 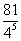 ، یعنی تا 0/079 کار می کند. اما احتمال این که دنباله برنده شود، با فرض این که چرخ دستکاری نشده و بنابراین همه چیز منصفانه و عادلانه است (که خلاصه یعنی )،
، یعنی تا 0/079 کار می کند. اما احتمال این که دنباله برنده شود، با فرض این که چرخ دستکاری نشده و بنابراین همه چیز منصفانه و عادلانه است (که خلاصه یعنی )، 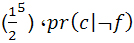 p است (این بار هم می توانید به حرف های من اعتماد کنید، البته اگر می خواهید)، یعنی تا 0/031 کار می کند. کم تر از 0/079 است. پس استنتاج معتبر است.
p است (این بار هم می توانید به حرف های من اعتماد کنید، البته اگر می خواهید)، یعنی تا 0/031 کار می کند. کم تر از 0/079 است. پس استنتاج معتبر است.فهمیدن روشی که بنابر آن احتمالات پیشین را به دست آوردیم مهم است. دو احتمال داشتیم: یا چرخ A دستکار شده یا چرخ B؛ هیچ اطلاعات دیگری هم نداشتیم تا بتوانیم میان دو احتمال فرق بگذاریم. پس یک احتمال را به آن ها نسبت دادیم. این نمونه ای است از کاربرد اصل عدم تفاوت(4)؛ بنابراین اصل، وقتی چند احتمال داریم که تفاوت خاصی میان آن ها نیست، همه ی آن ها به یک اندازه محتمل اند. پس اگرN احتمال داشته باشیم. احتمال هر یک
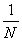 است اصل عدم تفاوت به نوعی از جنس اصل تقارن(5) است.
است اصل عدم تفاوت به نوعی از جنس اصل تقارن(5) است.توجه داشته باشید که این اصل را نمی توانستم دربرهان نظم به کار گیریم. در مورد دستگاه های رولت، دو موقعیتِ ممکن داشتیم که کاملاً متقارن بودند: چرخ A دستکاری شده، چرخ B دستکاری شده، در برهان نظم هم دو موقعیت در کار بود: خدای خالق وجود دارد، خدای خالق وجود ندارد. ولی تقارن این دوموقعیت فقط در این حد است که بگوییم: امروز دوشنبه است، امروز دوشنبه نیست. همان طور که دیدیم، موقعیت ها و جهان های ممکنی که در آن ها هیچ خالقی نیست بسیار بیش تر از آن موقعیت هایی است که خالق در آن ها وجود دارد.
اصل عدم تفاوت بخش مهمی از استدلال های شهودی ما در باب احتمالات است. اجازه دهید این مقاله را با ذکر این نکته تمام کنم که بگویم اصل عدم تفاوت هم خالی از ایراد نیست. حالا دیگر تقریباً همه می دانند که در بعضی از کاربردهای این اصل به تناقض دچار می شویم.
فرض کنید ماشینی بریزِبین را به مقصد شهری در فاصله ی 300 کیلومتری ترک می کند. متوسط سرعت ثابت ماشین بین km/h 50 و km/h 100 است. احتمال زمان رسیدن مسافر راچگونه توضیح دهیم؟ خب، اگر با km/h 100 برود، ساعت 3 بعداز ظهر می رسد؛ و اگر با سرعت km/h 50 برود، 6 بعداز ظهر می رسد. پس ساعتی بین این دو زمان می رسد. نقطه ی میانی این دو زمان 4:30 بعدازظهر است. بنابر اصل عدم تفاوت، همان قدر محتمل است که قبل از 4:30 برسد که بعد از آن. ولی سرعت میان km/h 50 و km/h 100، km/h 75 است. دوباره، بنابراین اصل، همان قدر محتمل است که ماشین ما بالای km/h 75 برود که زیر آن. اگر با سرعتkm/h 75 برود، 4 بعدازظهر می رسد. پس همان قدر محتمل است که قبل از 4 بعداز ظهر برسد که بعد از آن. پس احتمال این که قبل از 4:30 بعدازظهر برسد بیش تر از آن است که بعد از 4:30 برسد
خب، بس است! دنبالش را خودتان بگیرید. درباره ی احتمال در حد یک مقاله به قدر کافی پرچانگی کردم!
پی نوشت ها :
1-inverse probabilities
2- Prior Probabilities
3- a priori
4-Principle of Indifference
5- Symmetry Principle
پریست، گراهام،(1386)، منطق، مترجم: بهرام اسدیان، تهران: نشر ماهی، چاپ سوم
















